In diesem Beitrag definiere ich die Begriffe Ereignis und Gegenereignis in der Wahrscheinlichkeitsrechnung anhand anschaulicher Beispiele und Übungen. Außerdem gebe ich Tipps zum Vorgehen bei der Suche nach einem Gegenereignis.
Wir betrachten hierzu das einmalige Würfeln. Dabei besteht die Ergebnismenge aus 6 möglichen Ergebnissen: S = {1; 2; 3; 4; 5; 6}.
Die Erklärung der Menschenschreibweise hierzu findest du unter Einführung in die Mengenlehre.
Als Ereignis definieren wir anschließend A: Die geworfene Zahl ist gerade. Die Ergebnismenge besteht dabei aus 3 möglichen Ergebnissen: A = {2; 4; 6}. Sie ist eine Teilmenge der Ergnismenge. Deshalb schreibt man: A ⊂ S.
Im vorherigen Beitrag haben wir die Begriffe Ereignis und Ereignissmenge definiert. Hier nun eine andere
Definition Ereignis in der Wahrscheinlichkeitsrechnung:
Jede Teilmenge A, B, C, … der Ergebnismenge S eines Zufallsexperiments nennt man ebenfalls Ereignis. Deshalb schreibt man: A ⊂ S; B ⊂ S; C ⊂ S etc.
Beispiel zum Ereignis in der Wahrscheinlichkeitsrechnung:
Wir werfen eine Münze dreimal nacheinander. Dabei erscheint entweder die Zahl (Z) oder das Wappen (W).
Über das Baumdiagramm findet man dann die Ergebnismenge S:
![]()
A sei das Ereignis, das bei den drei Würfen mindestens 2 mal die Zahl geworfen wird. Wie lautet deshalb die Menge A?
![]()
Übung 1 zum Ereignis in der Wahrscheinlichkeitsrechnung:
B sei das Ereignis, dass keine Zahl erscheint. Wie lautet die Menge B?
Die Lösung hierzu ist unten.
Übung 2 zum Ereignis in der Wahrscheinlichkeitsrechnung:
C sei das Ereignis, dass höchstens einmal die Zahl erscheint. Wie lautet die Menge C?
Die Lösung hierzu ist unten.
Ereignisarten in der Wahrscheinlichkeitsrechnung erklärt an einem Glücksrad mit 8 Segmenten
Dabei steht in dem Glücksrad in jedem Segment eine Zahl zwischen 1 und 8.
![]()
![]()
Das Ereignis A tritt bei jeder Durchführung des Zufallsexperiments ein. Es wird deshalb sicheres Ereignis genannt. A = S.
![]()
Das Ereignis B enthält nur ein Element. Man nennt es daher Elementarereignis.
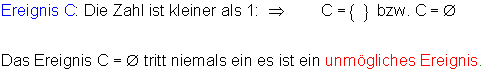
Definition Gegenereignis in der Wahrscheinlichkeitsrechnung
Das Gegenereignis ist sozusagen das Gegenteil des Ereignisses. Mit anderen Worten, es trifft ein, wenn das Ereignis nicht eintritt.

Beispiele zum Gegenereignis in der Wahrscheinlichkeitsrechnung
Am besten schreibt man sich zuerst alle möglichen Ereignisse auf. Wenn man dann die wird das Gegenereignis leichter klar.
| Ereignis | Gegenereignis |
| A: Höchstens 4 Autos sind defekt. Alle Möglichkeiten: 0; 1; 2; 3; 4; 5 etc. Autos sind defekt. Also sind bei A: 0; 1; 2; 3; 4 Autos defekt. |
\color{red}{\overline A} mehr als 4 Autos sind defekt. Das Gegenteil kann keine der Möglichkeiten 0 bis 4 sein, also müssen mindestens 5 Autos defekt sein.Dazu kannst du dir das 📽️Video Ereignis und Gegenereignis ansehen. |
| B: Mindestens 2 Handys wurden gestohlen Alle Möglichkeiten: 0; 1; 2 oder mehr Handys wurden gestohlen. Folglich wurden bei A: 2 oder mehr Handys gestohlen. |
\color{red}{\overline B} weniger als 2 Handys wurden gestohlen. Folglich wurde höchstens 1 Handy gestohlen. |
| C: Kein Auto ist blau Alle Möglichkeit: 0, 1 oder mehr Autos ist blau. Also sind bei A 0 Autos blau. |
Also können 1, 2, 3 etc. Autos blau sein. |
| D: Genau ein Apfel von drei Äpfeln ist faul Alle Möglichkeit: 0; 1; 2; 3 Äpfel sind faul. Folglich ist bei A: 1 Apfel faul. |
Folglich können hier 0, 2 oder 3 Äpfel faul sein. |
Die Beispiele B bis D kannst du dir in dem 📽️Video Ereignis und Gegenereignis Beispiele ansehen.
Das Gegenteil von ‚höchstens‘ und ‚kein‘ ist also ‚mindestens‘. Das Gegenteil von ‚genau 1‘ ist also ‚keins oder mehr als 1‘.
Vorgehen bei der Suche nach einem Gegenereignis in der Wahrscheinlichkeitsrechnung:
- Ergebnismenge S bestimmen.
- Ereignismenge bestimmen.
- Über die Restmengenbildung die Gegenereignismenge bilden.
Weil viele Probleme damit haben, hier ausführliche Beispiele:
Lösungsmöglichkeit für „Höchstens 4 Autos sind defekt“:
Der Einfachheit halber gehen wir von maximal 6 Autos aus. Alle Möglichkeiten der Kombinationen von heile (H) und defekt (D) bilden also die Ergebnismenge S.

Lösungsmöglichkeit für „Mindestens 2 Handys wurden gestohlen“.
Der Einfachheit halber gehen wir von maximal 4 Handys aus. Alle Möglichkeiten der Kombinationen von gestohlen (G) und nicht gestohlen (N) bilden folglich die Ergebnismenge S.

Lösungsmöglichkeit für „Kein Auto ist blau“.
Der Einfachheit halber gehen wir von maximal 4 Autos aus. Alle Möglichkeiten der Kombinationen von blau (B) und nicht blau (N) bilden dann die Ergebnismenge S.

Lösungsmöglichkeit für „Genau ein Apfel von drei Äpfeln ist faul“.
Wir müssen von 3 Äpfeln ausgehen. Alle Möglichkeiten der Kombinationen von faul (F) und nicht faul (N) bilden deshalb die Ergebnismenge S.

Lösung zu Übung 1
B sei das Ereignis, dass keine Zahl erscheint. Wie lautet die Menge B?
Lösung: ![]()
Bemerkung: Da die Menge B nur ein Element enthält, spricht man in diesem Fall von einem Elementarereignis.
Lösung zu Übung 2
C sei das Ereignis, dass höchstens einmal die Zahl erscheint. Wie lautet die Menge C?
Lösung: ![]()
Dazu findest du hier Aufgabe I.
Und Aufgaben zu Ereignissen und Verknüpfungen von Ereignissen II
Außerdem findest du hier eine Übersicht über alle Beiträge zum Thema Wahrscheinlichkeitsrechnung.
Dazu kannst auch den Wikipedia-Artikel zur Wahrscheinlichkeitsrechnung lesen.


