Hier sind die Lösungen der Aufgaben zu Zufallsexperiment I.
1. Eigenschaften von Zufallsexperimenten
Was verstehest du unter einem Zufallsexperiment? Nenne die wichtigsten Eigenschaften
Ausführliche Lösung:
Ein Zufallsexperiment ist ein Experiment mit folgenden Eigenschaften:
– Unter gleichen Bedingungen beliebig oft wiederholbar.
– Es gibt mindestens zwei mögliche Ergebnisse.
– Das Ergebnis ist nicht vorhersagbar.
2. Zufallsexperimente und Ergebnismenge
Gib vier Zufallsexperimente mit ihrer jeweiligen Ergebnismenge an.
Ausführliche Lösung:
Experiment und Lösungsmenge
- Einmaliger Wurf eines Würfels. S = {1; 2; 3; 4; 5; 6}
2. Einmaliger Wurf einer Münze. S = {Z; W}
3. Glücksrad mit 5 Sektoren der Nummern 1 bis 5, einmaliges drehen. S = {1; 2; 3; 4; 5}
4. Ziehung von 2 Kugeln aus einer Urne, die rote und schwarze Kugeln enthält. S = {rr; rs; sr; ss}
3. Tomaten
In einer Obstkiste befinden sich 10 rote Tomaten und 20 gelbe Tomaten gleicher Größe und gleicher Form. Dann werden aus der Kiste blind nacheinander drei Tomaten entnommen (ohne zurücklegen). Zeichne das Baumdiagramm und gib die Ergebnismenge S an.
Dazu kannst du dir das 📽️Video Baumdiagramm Ergebnismenge ansehen.
Ausführliche Lösung:
Baumdiagramm
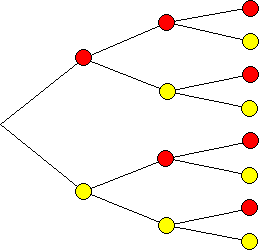
Ergebnismenge: S = {rrr, rrg;rgr;rgg; grr; grg; ggr; ggg}
4. Glasmurmeln
In einem Beutel befinden sich 5 gelbe, 3 rote und 4 blaue Glasmurmeln. Dem Beutel werden nacheinander 2 Murmeln entnommen (ohne zurücklegen). Zeichne das Baumdiagramm und gib die Ergebnismenge S an.
Ausführliche Lösung:
Baumdiagramm
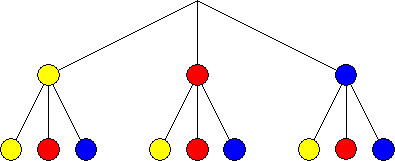
Ergebnismenge: S = {gg; gr; gb; rg; rr; rb; bg; br; bb}
5. Poolbillard
Zwei Schüler A und B spielen gegeneinander Poolbillard. Gewinner ist derjenige, der als erster zwei Spiele gewinnt.
Zeichne das Baumdiagramm und gib die Ergebnismenge S an.
Ausführliche Lösung:
Baumdiagramm
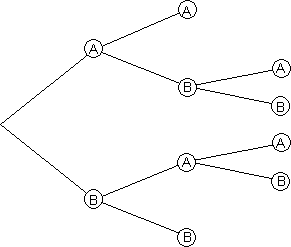
Ergebnismenge: S = {AA; ABA; ABB; BAA; BAB; BB}
6. Kugeln
Eine Schachtel enthält 2 rote Kugeln und 4 schwarze Kugeln. Aus der Schachtel werden blind nacheinander drei Kugeln entnommen (ohne zurücklegen). Zeichne das Baumdiagramm und gib die Ergebnismenge S an.
Ausführliche Lösung:
Baumdiagramm
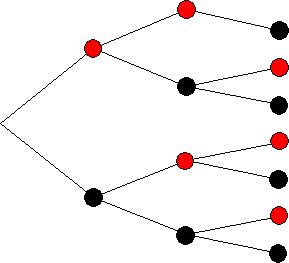
Ergebnismenge: S = {rrs; rsr; rss; srr; srs; ssr; sss}
7. Bonbons
In einer Tüte befinden sich 7 Bonbons. Davon sind 2 gelb und 5 rot. Nacheinander werden der Tüte 3 Bonbons entnommen (ohne zurücklegen).
Wie viele Möglichkeiten gibt es der Tüte Bonbons zu entnehmen?
Ausführliche Lösung:
Baumdiagramm
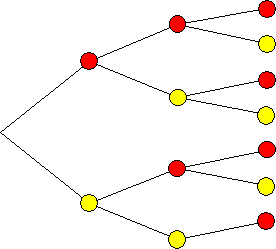
Ergebnismenge: S = {rrr; rrg; rgr; rgg; grr; grg; ggr}
Es gibt also 7 Möglichkeiten, der Tüte Bonbons zu entnehmen.
8. Zahlenschloss
Ein Zahlenschloss besteht aus drei Rädern mit den Zahlen 1 bis 9. Jemand kennt die Zahlen, die zum öffnen des Schlosses nötig sind, aber leider nicht die Reihenfolge. Wie viele Möglichkeiten gibt es. Zeichne ein Baumdiagramm. Die Zahlen lauten 3, 7 und 9.
Ausführliche Lösung:
Baumdiagramm
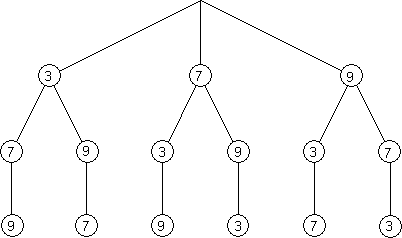
Ergebnismenge: S = {379; 397; 739; 793; 937; 973}
Es gibt also insgesamt 6 Möglichkeiten.
9. Glücksräder
Zwei Glücksräder bestehen aus je drei gleichgroßen Segmenten mit den Farben rot, blau und grün. Beide Räder werden gleichzeitig unabhängig voneinander in Drehung versetzt und nach einer bestimmten Zeit gleichzeitig gestoppt.
Skizziere die Glücksräder. Gib die Ergebnismenge unter der Bedingung an, dass das Ergebnis ( r , b ) nicht gleich dem Ergebnis ( b , r ) ist. Ist es für die Ergebnismenge entscheidend, ob die Räder gleichzeitig gestartet bzw. gestoppt werden? Begründe deine Antwort.
Ausführliche Lösung:
Baumdiagramm
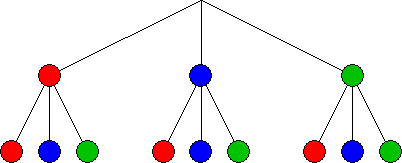
Ergebnismenge: S = {rr; rb; rg; br; bb; bg; gr; gb; gg}
Da sich beide Räder unabhängig voneinander drehen, spielt die Gleichzeitigkeit für Start oder Stopp für die Ergebnismenge keine Rolle. Man könnte auch ein Rad zweimal hintereinander laufen lassen.
10. Schülerrat
Der Schülerrat eines Berufskollegs besteht aus 3 Schülern und 2 Schülerinnen. Es wird ausgelost, wer in diesem Jahr Vorsitzender und Stellvertreter wird. Zuerst wird der Vorsitzende und dann der Stellvertreter ausgelost. Zeichne das Baumdiagramm und gib die Ergebnismenge S an.
Ausführliche Lösung:
Baumdiagramm
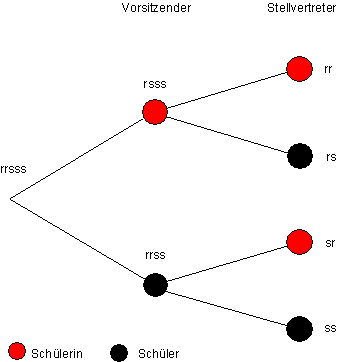
Ergebnismenge: S = {ww; wm; mw; mm}
Dabei bedeutet w Schülerin und m Schüler.
Hier findest du die Theorie hierzu.
Und hier die Aufgaben hierzu.
Hier findest du eine Übersicht über alle Beiträge zum Thema Wahrscheinlichkeitsrechnung, darin auch Links zu weiteren Aufgaben.

