Lösungen Hypothesentest Casio IV fx-CG50• 123mathe

Die hier dargestellten Lösungen der Hypothesentests mit dem Casio fx-CG50 sind Teilberechnungen, aus bestehenden Hypothesentestaufgaben, auf die an entsprechender Stelle verlinkt wird. Die Rechnungen wurden mit dem GTR Casio fx-CG20 durchgeführt. Abweichungen in den Ergebnissen sind darauf zurückzuführen, dass die Originalaufgaben mit Tabellenwerten entsprechender Binomialverteilungen, bzw. mit Näherungswerten der Normalverteilung berechnet wurden.

Eine Einführung in den Casio fx-CG20 und Casio fx-CG 50 findest du hier.

Update auf Casio fx-CG50

Wer noch den Casio fx-CG20 hat, kann sich auf der Webseite der Firma ein kostenloses Update herunterladen. Dann kannst du auch die neuen Funktionen des Casio fx-CG50 nutzen. Suche dazu auf Casio-Webseite nach ‚FX-CG20 & FX-CG50 Betriebssystem-Update‘. Ich gebe hier jedoch nicht den direkten Link ein, weil es in der Zwischenzeit vielleicht bereits ein neueres Update gibt.

A1. Nullhypothese: H₀: p ≤ 0,1 Alternativhypothese: H₁: p > 0,1

Signifikanzniveau: α ≤ 5%.
Bei einem Erhebungsumfang von n = 120 verzeichnet man k Erfolge.
Es handelt sich um einen rechtseitigen Hypothesentest, denn große Werte von k sprechen gegen H₀.

Ausführliche Lösung: Berechnung des Ablehnungsbereichs und Überprüfung des tatsächlichen Signifikanzniveaus.

Bei einer Anzahl von k = 19 oder mehr Erfolgen, würde die Nullhypothese abgelehnt und die Alternativhypothese angenommen werden.
Der dabei auftretende Fehler (Fehler 1. Art) wäre dann etwa 2,97%.Eingabeprozedur:

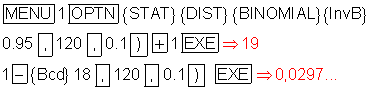
A2. Nullhypothese: H₀: p = 0,2 Alternativhypothese: H₁: p ≠ 0,2

Signifikanzniveau: α ≤ 10%.
Bei einem Erhebungsumfang von n = 100 verzeichnet man k Erfolge.
Es handelt sich um einen beidseitigen Hypothesentest, denn kleine, wie auch große Werte von k sprechen gegen H₀.

Ausführliche Lösung: Berechnung des Ablehnungsbereichs und Überprüfung des tatsächlichen Signifikanzniveaus.

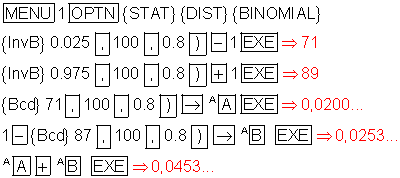
Ablehnungs-und Annahmebereich sehen dann wie folgt aus:
{ 0 … 13 } { 14 …. 20 … 27 } { 28 … 100 }

Fällt die Anzahl k der Erfolge in einen der beiden Ablehnungsbereiche, wird die Nullhypothese abgelehnt und die Alternativhypothese angenommen.
Der dabei auftretende Fehler (Fehler 1. Art) wäre dann etwa 8,1%.

Eingabeprozedur:

A3. Nullhypothese: H₀: p = 0,8 Alternativhypothese: H₁: p ≠ 0,8

Signifikanzniveau: α ≤ 5%.
Bei einem Erhebungsumfang von n = 100 verzeichnet man k Erfolge.
Es handelt sich um einen beidseitigen Hypothesentest, denn kleine, wie auch große Werte von k sprechen gegen H₀.

Ausführliche Lösung: Berechnung des Ablehnungsbereichs und Überprüfung des tatsächlichen Signifikanzniveaus.

Der rechte Ablehnungsbereich wird um eins erhöht. Dadurch ändern sich die Werte, rot in Klammern beschrieben.
Ablehnungs-und Annahmebereich sehen wie folgt aus:
{ 0 … 71 } { 72 …. 80 … 87 } { 88 … 100 }

Eingabeprozedur:

A4. Nullhypothese: H0: p ≥ 0,4 Alternativhypothese: H1: p < 0,4

Signifikanzniveau: α ≤ 5%.
Bei einem Erhebungsumfang von n = 2000 verzeichnet man k Erfolge.
Es handelt sich um einen linksseitigen Hypothesentest, denn große Werte von k sprechen gegen H₀.

Ausführliche Lösung: Linksseitiger Test:
Berechnung des Ablehnungsbereichs und Überprüfung des tatsächlichen Signifikanzniveaus.

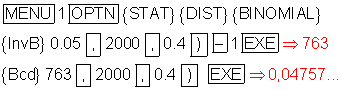
Bei einer Anzahl von k = 763 oder weniger Erfolge, würde die Nullhypothese abgelehnt und die Alternativhypothese angenommen werden.
Der dabei auftretende Fehler (Fehler 1. Art) wäre dann etwa 4,76%.Eingabeprozedur: