Für die Berechnung von Umgebungswahrscheinlichkeiten habe ich im letzten Beitrag die Tabelle normalverteilter Zufallsvariablen vorgestellt. Hier werde ich anhand einiger Beispiele den Umgang damit erklären. Dabei geht es um Intervalle symmetrisch zum Erwartungswert, Prozent-Umgebung vom Erwartungswert, Intervalle außerhalb von Umgebungen und asymmetrische Umgebungen.
Bitte beachte, dass die zu dem Wert z gehörige Umgebung immer symmetrisch zum Erwartungswert µ liegt!
- Intervall symmetrisch zum Erwartungswert
- Prozent-Umgebung vom Erwartungswert
- Intervalle außerhalb von Umgebungen
- Asymmetrische Umgebungen
Intervall Wahrscheinlichkeit symmetrisch zum Erwartungswert
Beispiel 1:
Gegeben ist ein n-stufiger Bernoulli-Versuch mit n = 500 und p = 0,33.
Bestimme dazu die Wahrscheinlichkeit für die Anzahl der Erfolge im Intervall [ 150 ; 180]! Rechne dabei mit einer Genauigkeit von drei Stellen hinter dem Komma!
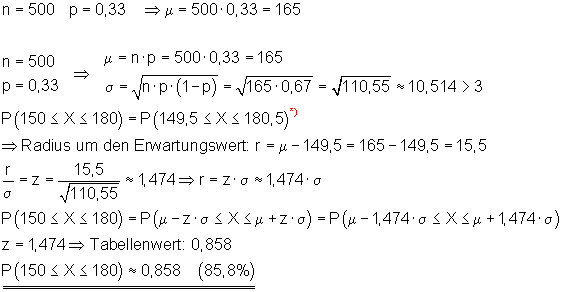
Ergebnis: Die Wahrscheinlichkeit für die Anzahl der Erfolge im Intervall [ 150 ; 180 ] beträgt also etwa 85,8%
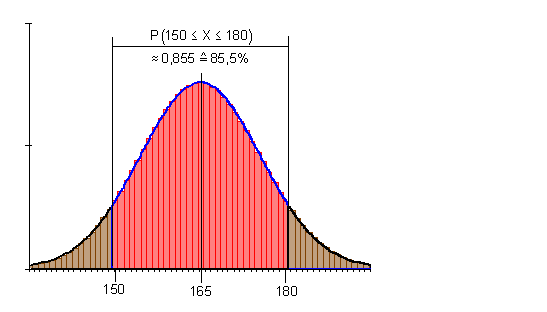
Warum sind die Intervallgrenzen um jeweils 0,5 zu vergrößern, wenn mit den Tabellenwerten der Normalverteilung die Intervallwahrscheinlichkeit bestimmt wird?
![]()
Die Daten der verwendeten Tabelle basieren auf der Normalverteilung. Würde man den Radius r = 165 – 150 = 15 wählen, dann wäre dieser um 0,5 zu klein. Er würde nur die halbe Fläche der Säule von k = 150 bzw. von k = 180 berücksichtigen. Dies erläutert die folgende Grafik:
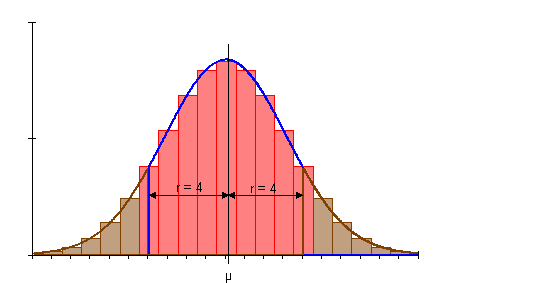
Der gewählte Radius r = 4 ist also zu klein. Er berücksichtigt auf jeder Seite vom Erwartungswert eine halbe Säule zu wenig. Dadurch wird die gewählte Umgebung nicht vollständig erfasst.
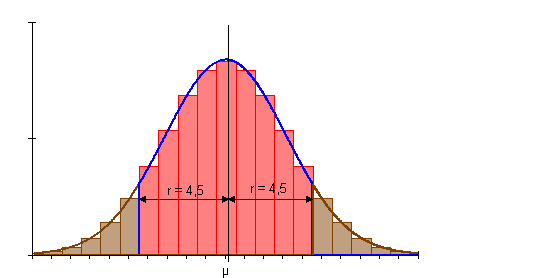
Der gewählte Radius r = 4,5 berücksichtigt diesmal auf jeder Seite vom Erwartungswert eine halbe Säule mehr, deshalb wird die gewählte Umgebung vollständig erfasst.
Prozent-Umgebung vom Erwartungswert
Beispiel 2:
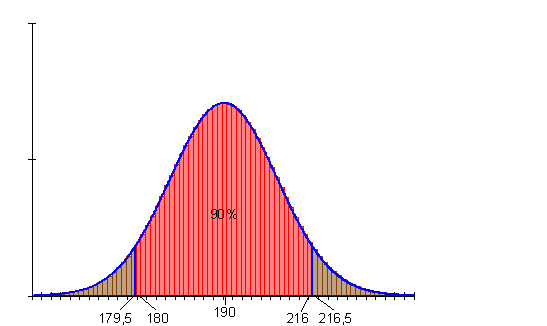
Bestimme die 90%- Umgebung vom Erwartungswert für n = 550 und p = 0,36.

Die Wahrscheinlichkeit für die Anzahl der Erfolge im Intervall [ 180 ; 216 ] beträgt also etwa 90%
Intervall Wahrscheinlichkeit außerhalb von Umgebungen
Beispiel 3
Gegeben ist ein n-stufiger Bernoulli-Versuch. Gesucht ist die Wahrscheinlichkeit für die Ergebnisse außerhalb von Umgebungen um den Erwartungswert.
a) ![]()
b) ![]()
zu a)
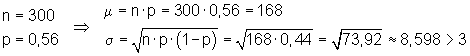
Zu bestimmen ist die Wahrscheinlichkeit für das Intervall [0 ; 161]. Aus der Tabelle kann nur die Wahrscheinlichkeit für ein um den Erwartungswert symmetrisches Intervall abgelesen werden, dieses enthält die Werte [162 …. 168 … 174 ]. Daran anschließend folgt das Intervall [175 …. 300], welches aus Symmetriegründen die gleiche Größe wie [0 ; 161] hat.
Es gilt dabei folgender Ansatz: [ { 0 … 161 } {162 … 168 … 174 } { 175 … 300}]
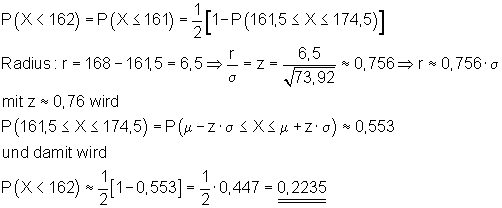
Die Wahrscheinlichkeit für weniger als 162 Erfolge ist also etwa 22,4%
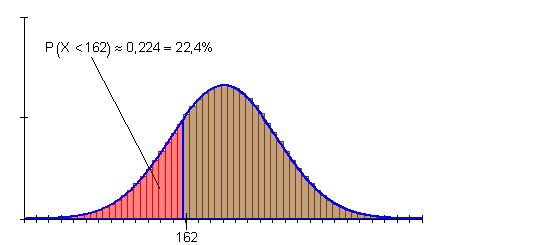
zu b)
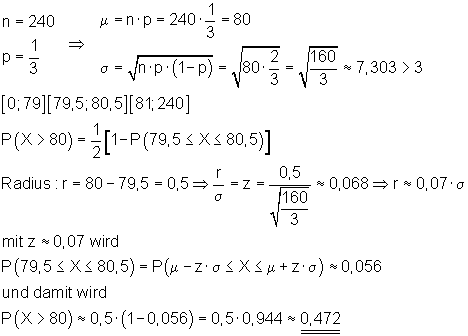
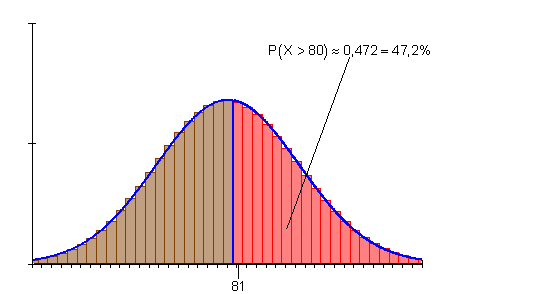
Die Wahrscheinlichkeit für mehr als 80 Erfolge ist deshalb etwa 47,2%
Berechnung einer asymmetrischen Umgebungswahrscheinlichkeit
Beispiel 3
Bestimme die Wahrscheinlichkeit einer nicht symmetrischen Umgebung vom Erwartungswert.
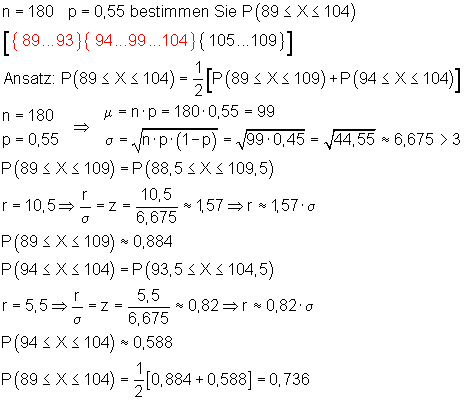
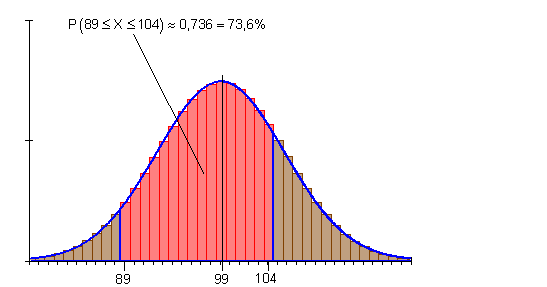
Die Wahrscheinlichkeit der Erfolge im Intervall [89 ; 104] ist daher etwa 73,6%.
Rechenhelfer für die Binomialverteilung
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Dazu findest du hier Aufgaben: Binominalverteilung I.
Außerdem Binominalverteilung II.
Hier findest du eine Übersicht über alle Beiträge zum Thema Wahrscheinlichkeitsrechnung. Darin auch Links zu Aufgaben.


