Binomialverteilung Normalverteilung • 123mathe

Als erstes stelle ich hier die Approximation der Binomialverteilung vor. Anschließend zeige ich einige Beispiele für die Gaußsche Normalverteilung. Danach stelle ich eine Tabelle der Wahrscheinlichkeiten für Sigma-Umgebungen normalverteilter Zufallsvariablen zur Verfügung. Anschließend werde ich den Umgang der Tabelle erklären. Am Ende findest du einen Rechenhelfer für die Binomialverteilung und den Link zu Aufgaben in weiteren Beiträgen.

Histogramme von Binomialverteilungen sind für nicht zu kleine n glockenförmig. Mit größer werdendem n tritt die Glockenform immer deutlicher hervor. Die Histogrammform nähert sich mit größer werdendem n immer mehr der Gaußschen Verteilungskurve, auch Glockenkurve genannt. Die gesamte Fläche zwischen der Kurve und der waagerechten Achse hat den Wert 1. Das gilt ebenso für die Summe aller Säulenflächen.

Approximation der Binomialverteilung durch die Gaußsche Normalverteilung

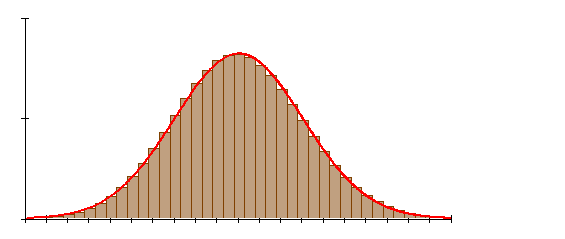
Dies ermöglicht es für große n, Wahrscheinlichkeiten in einem bestimmten Intervall näherungsweise zu bestimmen.

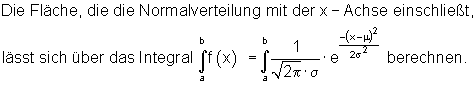
Die Berechnung der Fläche mit dem Integral ist recht mühsam, deshalb gibt es Tabellen in denen die Wahrscheinlichkeit von Sigma-Umgebungen aufgelistet sind.

Für Sigma-Umgebungen gilt folgender Zusammenhang:

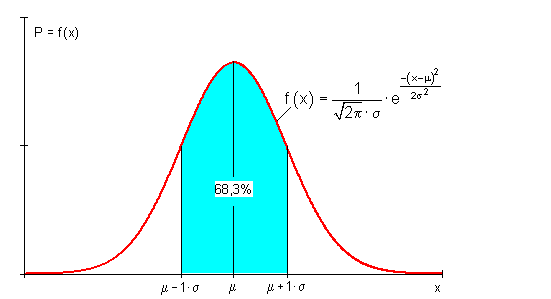
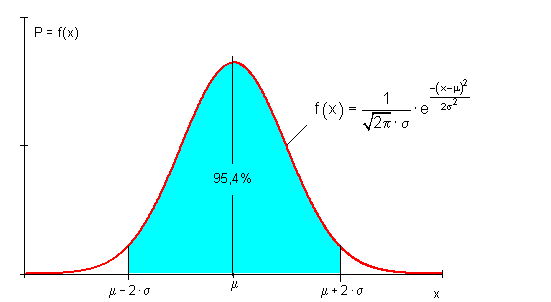
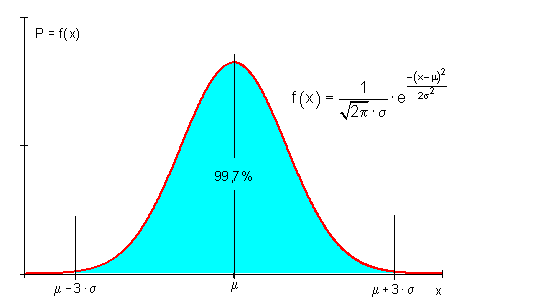
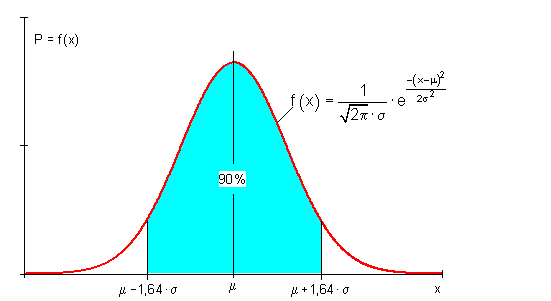
Für %- Umgebungen gilt folgender Zusammenhang:

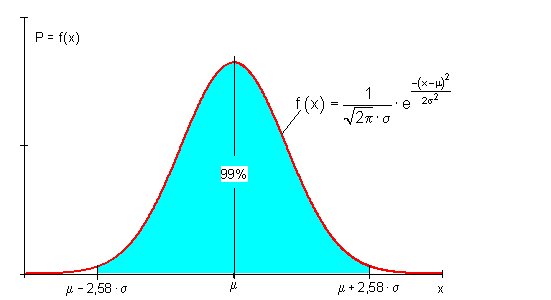
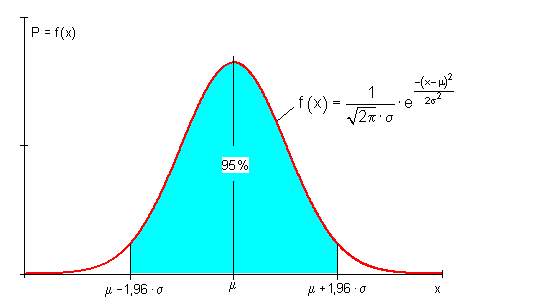
In der Literatur hat man sich auf folgende Umgebungswahrscheinlichkeiten geeinigt:

Die zu einem Radius gehörige Umgebungswahrscheinlichkeit

Der zu einer Umgebungswahrscheinlichkeit gehörige Radius

Da die Histogrammform der Binomialverteilung sich nur für entsprechend große n der Form der Normalverteilung immer mehr nähert, gilt folgendes Kriterium für die Verwendung der Intervallwahrscheinlichkeiten der Normalverteilung.

Laplace-Bedingung

Falls die Bedingung

erfüllt ist, liefert die Näherung durch die Normalverteilung hinreichend genaue Intervallwahrscheinlichkeiten.

Bislang war für jede Binomialverteilung mit einem bestimmten n und einer bestimmten Wahrscheinlichkeit p jeweils eine Tabelle mit den kumulierten Wahrscheinlichkeiten nötig, um Umgebungswahrscheinlichkeiten zu bestimmen. Falls nun die Werte einer Binomialverteilung die Laplace- Bedingung erfüllen, dürfen Tabellenwerte der Normalverteilung benutzt werden. Die Laplace- Bedingung ist in jedem Fall vorher zu überprüfen.

Für den Fall, dass der Umgebungsradius in Einheiten von Sigma angegeben wird, gilt folgender Zusammenhang:

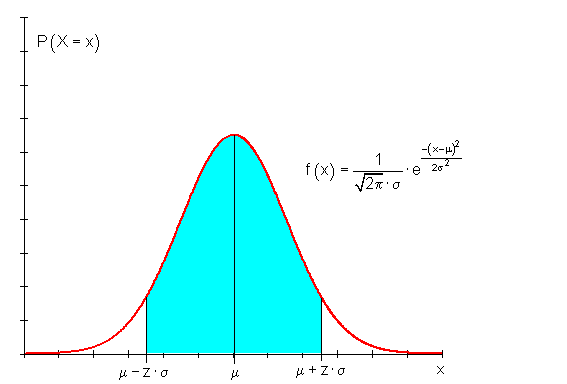
Der Umgebungsradius vom Erwartungswert wird als Vielfaches in Einheiten von Sigma ausgedrückt. Dabei ist z der Faktor, mit dem Sigma zu multiplizieren ist. Die Wahrscheinlichkeiten solcher Sigma- Umgebungen sind in der folgenden Tabelle in Abhängigkeit vom Faktor z dargestellt.

Der wesentliche Unterschied zur Darstellung der Wahrscheinlichkeiten in einer Binomialverteilung, wie sie bisher verwendet wurde, ist, dass in der Normalverteilung die Werte auf der x-Achse als kontinuierlich angesehen werden können. Bei der Binomialverteilung handelt es sich um diskrete Werte für k.

Normalverteilung:

Die Normalverteilung hat viele Namen. Sie wird auch Gaußsche Glockenkurve oder Gauß-Funktion genannt.

Tabelle: Wahrscheinlichkeiten
für Sigma-Umgebungen
normalverteilter Zufallsvariablen


z	P	z	P	z	P	z	P	z	P	z	P
0,01	0,008	0,51	0,390	1,01	0,688	1,51	0,869	2,01	0,956	2,51	0,988
0,02	0,016	0,52	0,397	1,02	0,692	1,52	0,871	2,02	0,957	2,52	0,988
0,03	0,024	0,53	0,404	1,03	0,697	1,53	0,874	2,03	0,958	2,53	0,989
0,04	0,032	0,54	0,411	1,04	0,702	1,54	0,876	2,04	0,959	2,54	0,989
0,05	0,040	0,55	0,418	1,05	0,706	1,55	0,879	2,05	0,960	2,55	0,989
0,06	0,048	0,56	0,425	1,06	0,711	1,56	0,881	2,06	0,961	2,56	0,990
0,07	0,056	0,57	0,431	1,07	0,715	1,57	0,884	2,07	0,962	2,57	0,990
0,08	0,064	0,58	0,438	1,08	0,720	1,58	0,886	2,08	0,962	2,58	0,990
0,09	0,072	0,59	0,445	1,09	0,724	1,59	0,888	2,09	0,963	2,59	0,990
0,10	0,080	0,60	0,451	1,10	0,729	1,60	0,890	2,10	0,964	2,60	0,991
0,11	0,088	0,61	0,458	1,11	0,733	1,61	0,893	2,11	0,965	2,61	0,991
0,12	0,096	0,62	0,465	1.12	0,737	1,62	0,895	2,12	0,966	2,62	0,991
0,13	0,103	0,63	0,471	1,13	0,742	1,63	0,897	2,13	0,967	2,63	0,991
0,14	0,111	0,64	0,478	1,14	0,746	1,64	0,899	2,14	0,968	2,64	0,992
0,15	0,119	0,65	0,484	1,15	0,750	1,65	0,901	2,15	0,968	2,65	0,992
0,16	0,127	0,66	0,491	1,16	0,754	1,66	0,903	2,16	0,969	2,66	0,992
0,17	0,135	0,67	0,497	1,17	0,758	1,67	0,905	2,17	0,970	2,67	0,992
0,18	0,143	0,68	0,503	1,18	0,762	1,68	0,907	2,18	0,971	2,66	0,993
0,19	0,151	0,69	0,510	1,19	0,766	1,69	0,909	2,19	0,971	2,69	0,993
0,20	0,159	0,70	0,516	1,20	0,770	1,70	0,911	2,20	0,972	2,70	0,993
0,21	0,166	0,71	0,522	1,21	0,774	1,71	0,913	2,21	0,973	2,71	0,993
0,22	0,174	0,72	0,528	1,22	0,778	1,72	0,915	2,22	0,974	2,72	0,993
0,23	0,182	0,73	0,535	1,23	0,781	1,73	0,916	2,23	0,974	2,73	0,994
0,24	0,190	0,74	0,541	1,24	0,785	1,74	0,918	2,24	0,975	2,74	0,994
0,25	0,197	0,75	0,547	1,25	0,789	1,75	0,920	2,25	0,976	2,75	0,994
0,26	0,205	0,76	0,553	1,26	0,792	1,76	0,922	2,26	0,976	2,76	0,994
0,27	0,213	0,77	0,559	1,27	0,796	1,77	0,923	2,27	0,977	2,77	0,994
0,28	0,221	0,78	0,565	1,28	0,799	1,78	0,925	2,28	0,977	2,78	0,995
0,29	0,228	0,79	0,570	1,29	0,803	1,79	0,927	2,29	0,978	2,79	0,995
0,30	0,236	0,80	0,576	1,30	0,806	1,80	0,928	2,30	0,979	2,80	0,995
0,31	0,243	0,81	0,582	1,31	0,810	1,81	0,930	2,31	0,979	2,81	0,995
0,32	0,251	0,82	0,588	1,32	0,813	1,82	0,931	2,32	0,980	2,82	0,995
0,33	0,259	0,83	0,593	1,33	0,816	1,83	0,933	2,33	0,980	2,83	0,995
0,34	0,266	0,84	0,599	1,34	0,820	1,84	0,934	2,34	0,981	2,84	0,995
0,35	0,274	0,85	0,605	1,35	0,823	1,85	0,936	2,35	0,981	2,85	0,996
0,36	0,281	0,86	0,610	1,36	0,826	1,86	0,937	2,36	0,982	2,86	0,996
0,37	0,289	0,87	0,616	1,37	0,829	1,87	0,939	2,37	0,982	2,87	0,996
0,38	0,296	0,88	0,621	1,38	0,832	1,88	0,940	2,38	0,983	2,88	0,996
0,39	0,303	0,89	0,627	1,39	0,835	1,89	0,941	2,39	0,983	2,89	0,996
0,40	0,311	0,90	0,632	1,40	0,838	1,90	0,943	2,40	0,984	2,90	0,996
0,41	0,318	0,91	0,637	1,41	0,841	1,91	0,944	2,41	0,984	2,91	0,996
0,42	0,326	0,92	0,642	1,42	0,844	1,92	0,945	2,42	0,984	2,92	0,996
0,43	0,333	0,93	0,648	1,43	0,847	1,93	0,946	2,43	0,985	2,93	0,997
0,44	0,340	0,94	0,653	1,44	0,850	1,94	0,948	2,44	0,985	2,94	0,997
0,45	0,347	0,95	0,658	1,45	0,853	1,95	0,949	2,45	0,986	2,95	0,997
0,46	0,354	0,96	0,663	1,46	0,856	1,96	0,950	2,46	0,986	2,96	0,997
0,47	0,362	0,97	0,668	1,47	0,858	1,97	0,951	2,47	0,986	2,97	0,997
0,48	0,369	0,98	0,673	1,48	0,861	1,98	0,952	2,48	0,987	2,98	0,997
0,49	0,376	0,99	0,678	1,49	0,864	1,99	0,953	2,49	0,987	2,99	0,997
0,50	0,383	1,00	0,683	1,50	0,866	2,00	0,954	2,50	0,988	3,00	0,997

Umgang mit der Tabelle normalverteilter Zufallsvariablen
Intervalle und Wahrscheinlichkeiten

1. Intervall ist symmetrisch zum Erwartungswert.

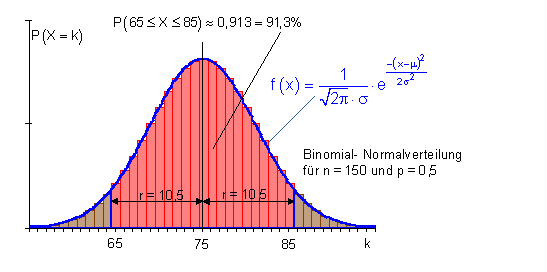
2. Intervall für höchstens k Erfolge.

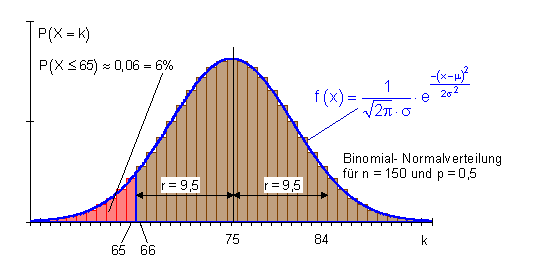
3. Intervall für mindestens k Erfolge.

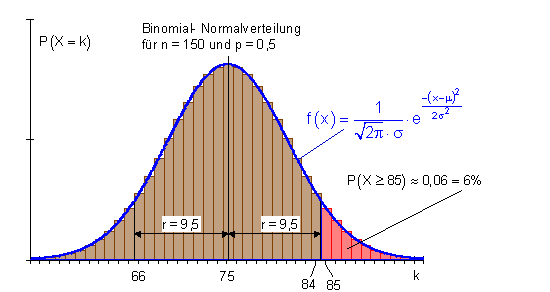
4. Intervall ist nicht symmetrisch zum Erwartungswert.

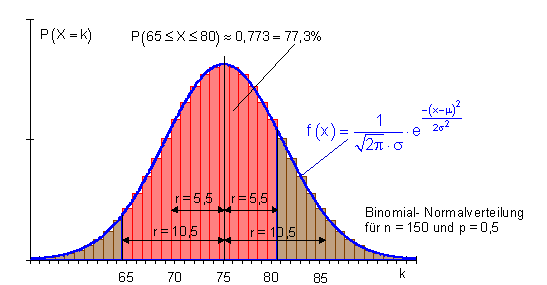
5. Berechnung des Radius einer Umgebung bei vorgegebener Umgebungswahrscheinlichkeit.

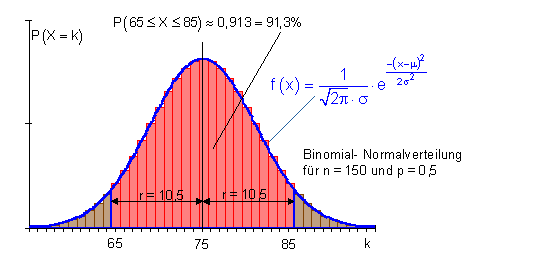
6. Zur Berechnung anderer Umgebungswahrscheinlichkeiten verfährt man in ähnlicher Weise. (Hier 95%- Umgebung)

Rechenhelfer für die Binomialverteilung

Dazu findest du hier Aufgaben: Binominalverteilung I.

Außerdem Binominalverteilung II.

Und Binominalverteilung III.

Hier findest du eine Übersicht über alle Beiträge zum Thema Wahrscheinlichkeitsrechnung, darin auch Links zu Aufgaben.

Approximation der Binomialverteilung durch die Normalverteilung

Approximation der Binomialverteilung durch die Gaußsche Normalverteilung