In diesem Beitrag beschäftige ich mich mit den Umgebungswahrscheinlichkeiten in Binomialverteilungen. Dazu stelle ich mehrere Beispiele vor. Danach erläutere ich die Wahrscheinlichkeit der einfachen, doppelten und dreifachen Sigma-Umgebung. Schließlich zeige ich, was passiert, wenn ich der Umgebung des Erwartungswerts einen Radius zuordne.
Erwartungswert
Bei einer Binomialverteilung ist der Erwartungswert der mit der größten Wahrscheinlichkeit. In der Umgebung des Erwartungswertes befinden sich die Anzahlen der Erfolge mit den höchsten Wahrscheinlichkeiten. Je mehr die Anzahl der Erfolge sich vom Erwartungswert unterscheiden, desto geringer wird deren Wahrscheinlichkeit. Wir interessieren uns zunächst für die nähere Umgebung des Erwartungswertes und die in diesem Bereich auftretenden Wahrscheinlichkeiten. Folgende Verteilung soll als Beispiel dienen:
Beispiel 1
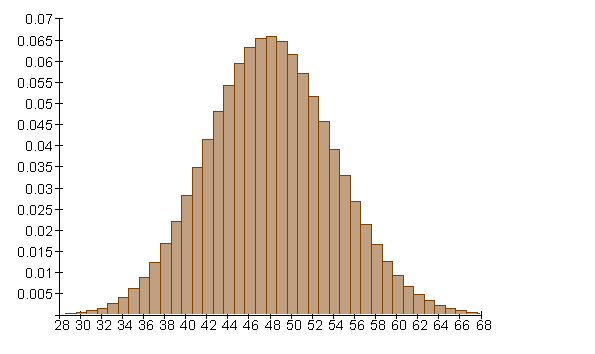
Wahrscheinlichkeit einer Sigma-Umgebung
Um dies zu untersuchen, zeichnen wir um den Erwartungswert 48 drei Umgebungen ein.

In diesem Bereichen untersuchen wir danach die Wahrscheinlichkeit.
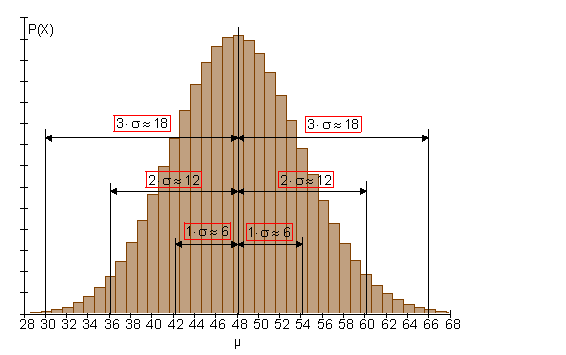
Dazu benötigen wir zunächst eine kumulierte Wahrscheinlichkeitstabelle für den interessierenden Bereich.
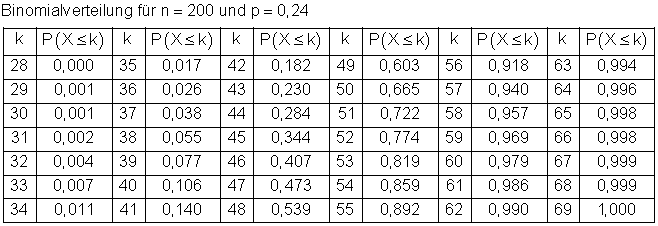
Wahrscheinlichkeit der einfachen Sigma-Umgebung
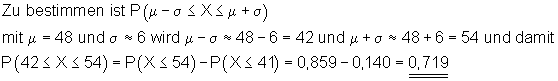
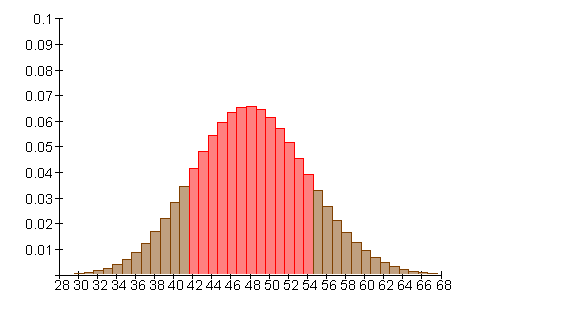
Mit einer Wahrscheinlichkeit von etwa 0,719 (71,9%) liegt die Anzahl der Erfolge im Intervall [ 42 ; 54 ]. Das entspricht etwa der einfachen Sigma-Umgebung des Erwartungswertes.
![]()
Wahrscheinlichkeit der doppelten Sigma-Umgebung
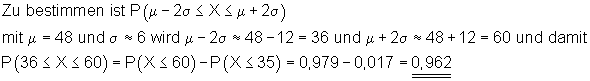
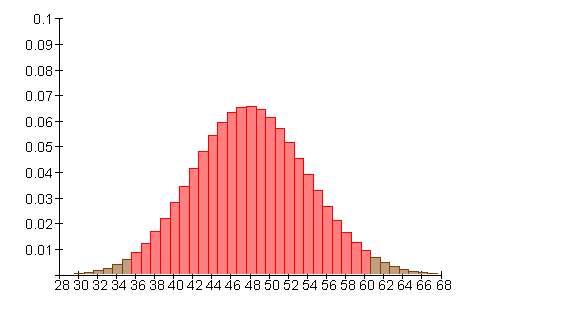
Mit einer Wahrscheinlichkeit von etwa 0,962 (96,2%) liegt die Anzahl der Erfolge im Intervall [ 36 ; 60 ]. Das entspricht etwa der doppelten Sigma-Umgebung des Erwartungswertes.
![]()
Wahrscheinlichkeit der dreifachen Sigma-Umgebung
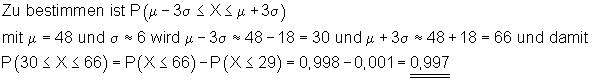
Mit einer Wahrscheinlichkeit von etwa 0,997 (99,7%) liegt die Anzahl der Erfolge im Intervall [ 30 ; 66 ]. Das entspricht etwa der dreifachen Sigma-Umgebung des Erwartungswertes.
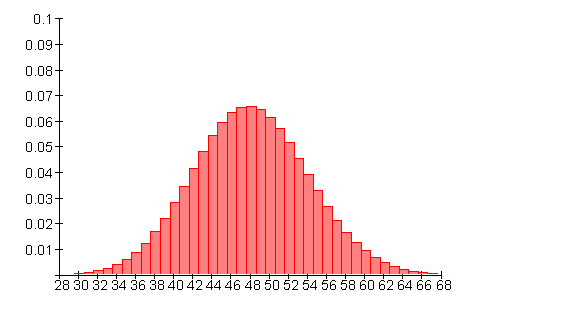
![]()
Umgebungsradius
Nun ordnen wir der Umgebung des Erwartungswerts einen Radius zu. Darunter verstehen wir den beidseitigen Abstand vom Erwartungswert.
Eine Grafik erläutert das.

Jedem Umgebungsradius können wir eine bestimmte Wahrscheinlichkeit zuordnen.
Im oben angeführten Beispiel gehört zu einer einfachen Sigma- Umgebung (r = 6) eine Umgebungswahrscheinlichkeit von etwa 0,719. Zur doppelten Sigma- Umgebung ( r = 12) eine von etwa 0,962. Zur dreifachen Sigma- Umgebung (r = 18) schließlich eine von etwa 0,997.
Umgekehrt gehört zu jeder Umgebungswahrscheinlichkeit ein bestimmter Radius.
Der Umgebungsradius bei fest vorgegebener Umgebungswahrscheinlichkeit (90%, 95%, 99%) kann man wie folgt bestimmen:
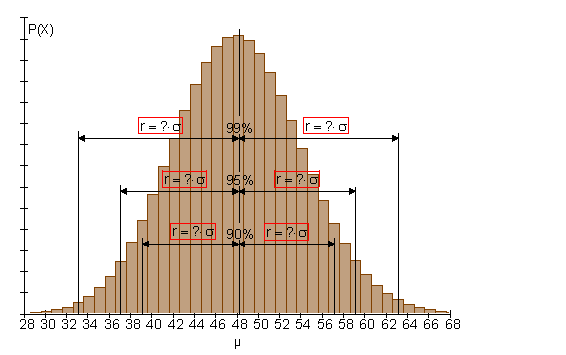
Liegt für die Binomialverteilung eine Tabelle mit den kumulierten Wahrscheinlichkeiten vor, lässt sich das Problem durch Einschachtelung lösen. Für die zwei Sigma-Umgebung, (im obigen Beispiel r = 12), war die Umgebungswahrscheinlichkeit etwa 96,2%.
Für die 90% Wahrscheinlichkeit ist der Umgebungsradius geringer.
Ansatz mit r = 10.

Der gesuchte Radius liegt zwischen den Werten 9 und 10. Da es sich bei der Binomialverteilung um eine diskrete Verteilung handelt, muss man sich für den Radius entscheiden, der der gewünschten Wahrscheinlichkeit am nächsten liegt. In diesem Fall ist das der Radius r = 9. Teilt man diesen Wert durch Sigma, dann lässt sich der Radius als vielfaches von Sigma darstellen.
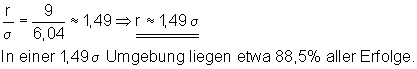
![]()
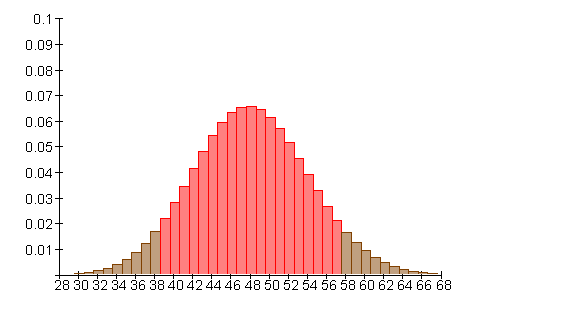
Für die 95% Wahrscheinlichkeit wird der Ansatz mit r = 12 versucht.

Der gesuchte Radius liegt zwischen den Werten 11 und 12. Der Radius r = 11 liegt der gewünschten Wahrscheinlichkeit am nächsten.
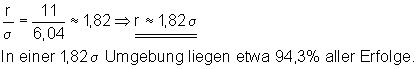
![]()
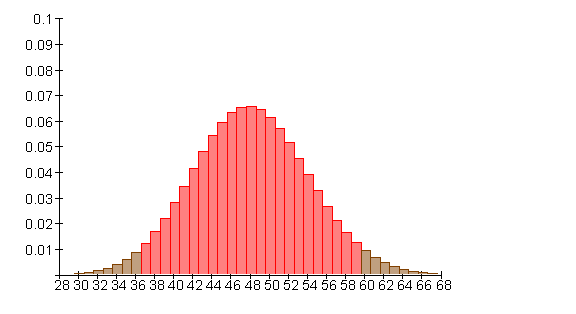
Für die 99% Wahrscheinlichkeit wird der Ansatz mit r = 14 versucht.

Der gesuchte Radius hat den Wert r = 15.
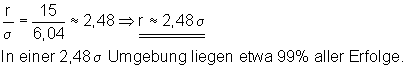
![]()
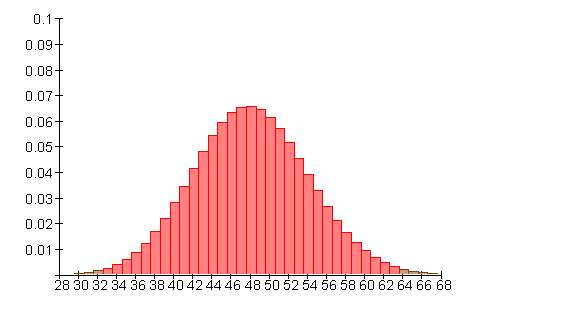
Dazu findest du hier eine Übersicht über alle Beiträge zum Thema Wahrscheinlichkeitsrechnung. Darin auch Links zu Aufgaben.


