
Hier findest du die Lösungen zu den Aufgaben zur Binomialverteilung und Lösungen Binominalverteilung.
1.
Erkläre die Begriffe Bernoulli-Experiment, Trefferwahrscheinlichkeit, Bernoullikette und Länge einer Bernoullikette.
1. Ausführliche Lösung:
Ein Bernoulli-Experiment ist ein Zufallsexperiment, das nur zwei Ergebnisse hat. Die Ergebnisse werden Erfolg (Treffer) oder Misserfolg (kein Treffer) genannt.
Die Trefferwahrscheinlichkeit ist die Wahrscheinlichkeit für einen Treffer (p).
Eine Bernoullikette entsteht, wenn dasselbe Bernoulli-Experiment mehrmals nacheinander ausgeführt wird.
Die Länge einer Bernoullikette gibt an, wie oft das einzelne Experiment nacheinander ausgeführt wird.
Beispiel:
Eine Münze wird 100 mal nacheinander geworfen. Der Münzwurf ist ein Bernoulli-Experiment, es gibt zwei Ergebnisse, Zahl und Kopf. Die Trefferwahrscheinlichkeit ist p = 0,5. Da der Münzwurf 100 mal wiederholt wird, spricht man bei diesem Experiment von einer Bernoullikette. Die Länge dieser Bernoullikette beträgt n = 100.
2.
Bei welchen der folgenden Zufallsexperimente handelt es sich um Bernoulliketten? Gib, wenn möglich, die Trefferwahrscheinlichkeit p und die Länge n der Bernoullikette an.
a) Wir werfen einen Würfel dreimal und notieren die Anzahl der Sechsen.
b) Wir werfen einen Würfel dreimal und notieren die Augensumme.
c) Wir nehmen aus einer Urne mit 3 weißen und 7 roten Kugeln so lange ohne Zurücklegen Kugeln, bis die erste rote Kugel erscheint.
d) Wir nehmen aus einer Urne mit 3 weißen und 7 roten Kugeln 4-mal mit Zurücklegen jeweils eine Kugel.
e) Bei einem Glücksrad erscheint in 50% aller Fälle eine 1, in jeweils 25% der Fälle eine 2 bzw. eine 3. Wir drehen das Rad viermal und notieren die Ziffern als 4-stellige Zahl.
f) Wir drehen das Glücksrad aus (e) achtmal. Jedes Mal, wenn die 3 erscheint, erhält man 10 Cent.
g) Wir drehen das Glücksrad aus (e) so oft, bis die 3 erscheint, höchstens jedoch fünfmal.
2. Ausführliche Lösungen
a) Es handelt sich um eine Bernoullikette der Länge n = 3. Als Treffer bezeichnet man das Ereignis 6. Die Trefferwahrscheinlichkeit ist in jeder Stufe gleich p = 1/6.
b) Es handelt sich um keine Bernoullikette, da es in jeder Stufe 6 verschiedene Ergebnisse geben kann. { 1; 2 ; 3 ; 4 ; 5 ; 6 }. Für eine Bernoullikette dürften es nur zwei sein.
c) Es handelt sich um keine Bernoullikette, da die Kugeln nicht zurückgelegt werden und sich dadurch die Wahrscheinlichkeit von Stufe zu Stufe ändert. Für eine Bernoullikette muss die Wahrscheinlichkeit für einen Treffer in jeder Stufe gleich sein.
d) Es handelt sich um eine Bernoullikette der Länge n = 4. Die Wahrscheinlichkeit für Treffer weiß ist durch das Zurücklegen konstant p = 3/10, für Treffer rot p = 7/10.
e) Es handelt sich um keine Bernoullikette, da es in jeder Stufe drei Ergebnisse geben kann { 1 ; 2 ; 3 }. Für eine Bernoullikette darf es nur zwei Ergebnisse pro Stufe geben.
f) Es handelt sich um eine Bernoullikette der Länge n = 8. Als Treffer wird die Zahl 3 mit p = 0,25 festgelegt. In jeder Stufe bleibt die Wahrscheinlichkeit konstant.
g) Es handelt sich um eine Bernoullikette mit nichtfestgelegter Länge. Als Treffer wird die Zahl 3 mit der Wahrscheinlichkeit p = 0,25 festgelegt. Die maximale Kettenlänge beträgt 5.
3.
Ein Glücksrad hat 3 gleich große Sektoren mit den Symbolen Kreis, Kreuz und Stern. Wir drehen es viermal. Wie groß ist die Wahrscheinlichkeit für folgende Ereignisse?
A: Es tritt dreimal Stern auf.
B: Es tritt mindestens dreimal Stern auf.
C: Es tritt höchstens einmal Stern auf.
D: Es tritt höchstens dreimal Stern auf.
3. Ausführliche Lösungen
Hier findest du die Lösungen mit dem Casio fx-CG 20 und Casio fx-CG 50 hierzu.
A: Die Wahrscheinlichkeit dafür, dass genau dreimal Stern auftritt, ist 0,0988.
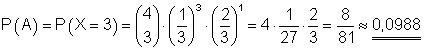
B: Die Wahrscheinlichkeit dafür, dass mindestens dreimal Stern auftritt, ist 0,1111….
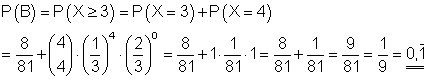
C: Die Wahrscheinlichkeit dafür, dass höchstens einmal Stern auftritt, ist 0,5926.
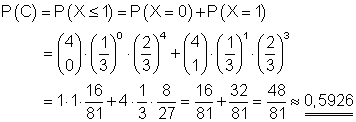
D: Die Wahrscheinlichkeit dafür, dass höchstens dreimal Stern auftritt, ist 0,9877.
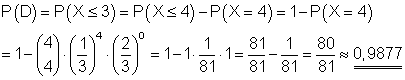
4.
Von einer großen Ladung Apfelsinen sind 20% verdorben. Wir entnehmen 5 Stück. Wie groß ist die Wahrscheinlichkeit für folgende Ereignisse:
A: Eine Apfelsine ist verdorben.
B: Alle Apfelsinen sind in Ordnung.
C: Mindestens zwei Apfelsinen sind verdorben.
4. Ausführliche Lösungen
Hier findest du die Lösungen mit dem Casio fx-CG 20 und Casio fx-CG 50 hierzu.
![]()
A: Die Wahrscheinlichkeit dafür, dass genau eine Apfelsine verdorben ist, ist 0,4096.
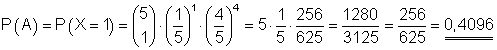
B: Alle Apfelsinen sind in Ordnung, bedeutet, keine Apfelsine ist verdorben.
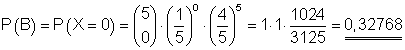
Die Wahrscheinlichkeit dafür, dass alle Apfelsinen in Ordnung sind, ist 0,32768.
C: Die Wahrscheinlichkeit dafür, dass mindestens zwei Apfelsinen verdorben sind, ist 0,26272.
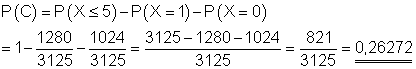
5.
Die Wahrscheinlichkeit für die Geburt eines Mädchens beträgt 0,49, für die Geburt eines Jungen 0,51.
Wie groß ist die Wahrscheinlichkeit, dass in einer Familie mit 4 Kindern
A: genau zwei Mädchen sind?
B: höchstens 3 Mädchen sind?
5. Ausführliche Lösungen
Hier findest du die Lösungen mit dem Casio fx-CG 20 und Casio fx-CG 50 hierzu.
A: Die Wahrscheinlichkeit dafür, dass in der Familie genau zwei Mädchen sind, ist 0,3747.
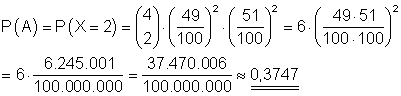
B: Die Wahrscheinlichkeit dafür, dass in der Familie höchstens drei Mädchen sind, ist 0,9424.
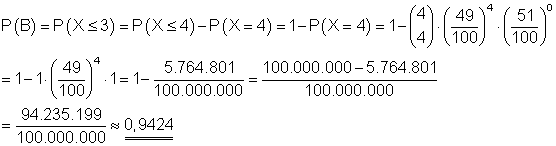
6.
Wie oft muss man eine Münze mindestens werfen, um mit einer Wahrscheinlichkeit von mindestens 99% mindestens einmal Kopf zu erhalten?
6. Ausführliche Lösung
Hier findest du die Lösungen mit dem Casio fx-CG 20 und Casio fx-CG 50 hierzu.
Die Wahrscheinlichkeit für Kopf und Zahl sei gleich ( p = 0,5).Das Gegenereignis von mindestens einmal Kopf ist keinmal Zahl.
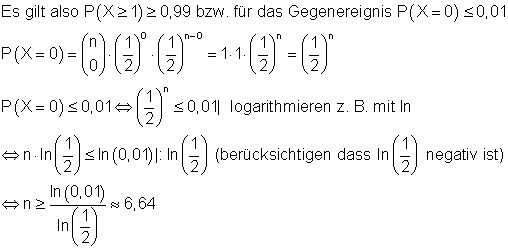
Die Münze muss mindestens 7 mal geworfen werden, um mit einer Sicherheit von mindestens 99% mindestens einmal Kopf zu erhalten.
7.
Wie oft muss man mindestens Würfeln, um mit einer Wahrscheinlichkeit von mindestens 90% mindestens eine Sechs zu bekommen?
7. Ausführliche Lösung
Hier findest du die Lösungen mit dem Casio fx-CG 20 und Casio fx-CG 50 hierzu.
A: Mindestens eine 6 bei n Würfen. E = { 1; 2 ; 3 ; … n } p = 1/6
Das Gegenereignis von A lautet: Keine 6 bei n Würfen.
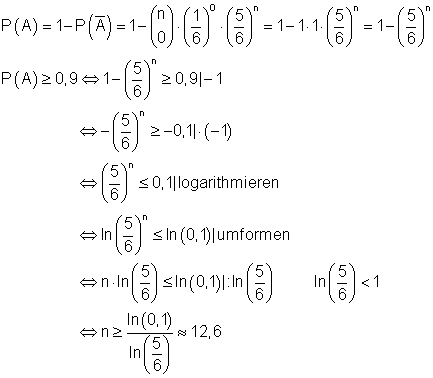
Man muss mindestens 13 mal würfeln, um mit einer Wahrscheinlichkeit von mindestens 90% mindestens eine 6 zu werfen.
8.
Wir werfen einen Würfel 60 mal. Wie groß ist die Wahrscheinlichkeit für folgende Ereignisse:
A: Man wirft genau 10 mal die 6.
B: Man wirft mindestens 10 mal die 6.
C: Man wirft höchstens 10 mal die 6.
D: Die Anzahl der geworfenen Sechser liegt zwischen 6 und 12 einschließlich.
E: Man wirft mehr als 4 und weniger als 15 Sechser.
F: Die Augenzahl ist in weniger als 25 Fällen ungerade.
G: Die Augenzahl ist in mehr als 30 Fällen gerade.
H: Es treten mehr als 25 und weniger als 35 ungerade Augenzahlen auf.
8. Ausführliche Lösungen
Hier findest du die Lösungen mit dem Casio fx-CG 20 und Casio fx-CG 50 hierzu.


A: Man wirft genau 10 mal die 6.
![]()
B: Man wirft mindestens 10 mal die 6.
![]()
C: Man wirft höchstens 10 mal die 6.
![]()
D: Die Anzahl der geworfenen Sechser liegt zwischen 6 und 12 einschließlich.
![]()
E: Man wirft mehr als 4 und weniger als 15 Sechser.
![]()
F: Die Augenzahl ist in weniger als 25 Fällen ungerade.
![]()
G: Die Augenzahl ist in mehr als 30 Fällen gerade.
![]()
H: Es treten mehr als 25 und weniger als 35 ungerade Augenzahlen auf.
![]()
Hier findest du die Aufgaben hierzu.
Hier findest du eine Übersicht über alle Beiträge zum Thema Wahrscheinlichkeitsrechnung, darin auch Links zu den Aufgaben Binominalverteilung II bis V.

