Hier findest du die Lösungen der Aufgaben zur Differenzialrechnung aus der Praxis mit komplettem Lösungsweg.
1.
Anwendungsaufgabe aus der Landwirtschaft (Biologie)
In der Landwirtschaft wird die Reaktionsstärke R auf ein Düngemittel in Abhängigkeit von der gegebenen Menge x (Dosis) durch Funktionen dritten Grades R(x) beschrieben. Die momentane Änderungsrate der Reaktionsstärke ist ein Maß für die Empfindlichkeit der Pflanze auf die verabreichte Dosis x. Eine Testreihe ergab bei einer Dosis von x = 0 Einheiten die Reaktionsstärke Null ; bei x = 2 zwei ; bei x = 4 vier und bei x = 6 Null Reaktionseinheiten.
Ausführliche Lösung:
a) Bestimme die Funktion R(x) in Abhängigkeit von der Dosis x.
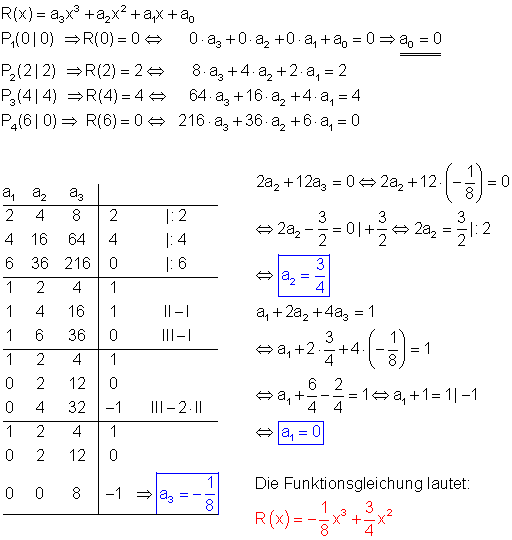
b)
Funktionswerte für x = 1 ; 3 ; und 5
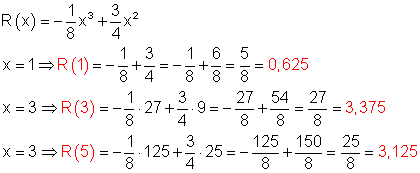
c) Für welchen Dosiswert ist die Reaktion am stärksten?
Gesucht ist die maximale Reaktionsstärke in Abhängigkeit von der Dosis. Die maximale Reaktionsstärke entspricht dem Maximum von R(x).
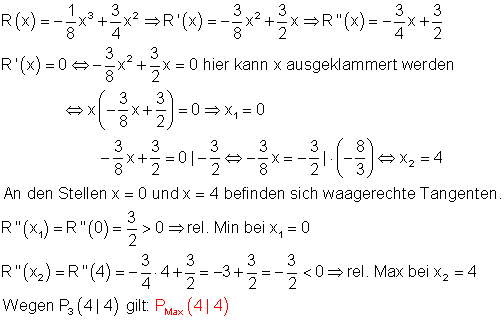
Für einen Dosiswert von x = 4 ist die Reaktion am stärksten.
d) Bei welcher Dosis reagiert die Pflanze am empfindlichsten auf das Düngemittel?
Die momentane Änderungsrate von R(x) ist ein Maß für die Empfindlichkeit der Pflanze auf das Düngemittel. Da die momentane Änderungsrate einer Funktion deren Steigung entspricht, wird der Dosiswert x gesucht, bei der die Steigung des Graphen von R(x) maximal ist. Der Wendepunkt kennzeichnet den Punktmit maximaler, bzw. minimaler Steigung.
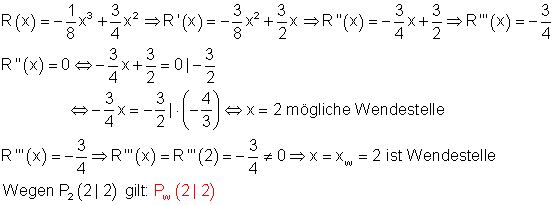
Bei einen Dosiswert von x = 2 reagiert die Pflanze am empfindlichsten auf das Düngemittel.
e) Bestimme die Achsenschnittpunkte.

f) Trage alle bisher bekannten Werte in eine Wertetabelle ein.
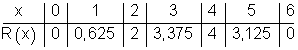
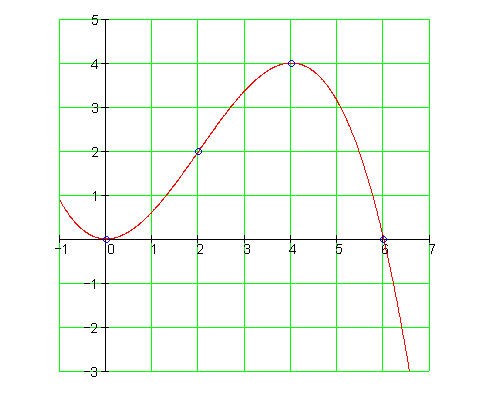
g) Zeichne den Graphen in ein geeignetes Koordinatensystem.
h) P1 ( 0 | 0 ) Wird kein Düngemittel gegeben, ist auch keine Reaktion der Pflanze zu erwarten.
PMax ( 4 | 4 ) Bei der Dosis x = 4 ist die Reaktion der Pflanze am stärksten (Düngungsoptimum). Wird mehr gegeben, so spricht man von Überdüngung mit geringerem Erfolg.
Pw ( 2 | 2 ) Die Empfindlichkeit der Pflanze auf Dünger ist bei der Dosis x = 2 am stärksten. Dort bewirken geringste Dosisverstärkungen die stärkste Reaktionszunahme.
P4 ( 6 | 0 ) Bei der Dosis x = 6 erfolgt keine Reaktion der Planze mehr. Für x > 6 ist das Ergebnis schlechter als ohne Düngung. Die Pflanze würde sich zurückentwickeln, bzw. absterben.
Aus Kostengründen würde der Landwirt sich möglicherweise für eine Dosierung im Bereich 2 < x < 4 entscheiden.
2.
Anwendungsaufgabe aus der Medizin (Radiologie)
In der Krebstherapie wird die Effizienz E einer Bestrahlung in Abhängigkeit von der gegebenen Dosis x näherungsweise durch Funktionen dritten Grades E(x) beschrieben. Die Steigung des Graphen von E(x) ist ein Maß für die Effizienzänderung in Abhängigkeit von der Dosis x. Eine Testreihe ergab bei einer Dosis von x = 1 Dosiseinheiten die Effizienz 5/4 ; bei x = 2 vier ; bei x = 4 acht und bei x = 5 25/4 Effizienzeinheiten.
Ausführliche Lösung:
a) Bestimme die Funktion E(x) in Abhängigkeit von der Dosis x!
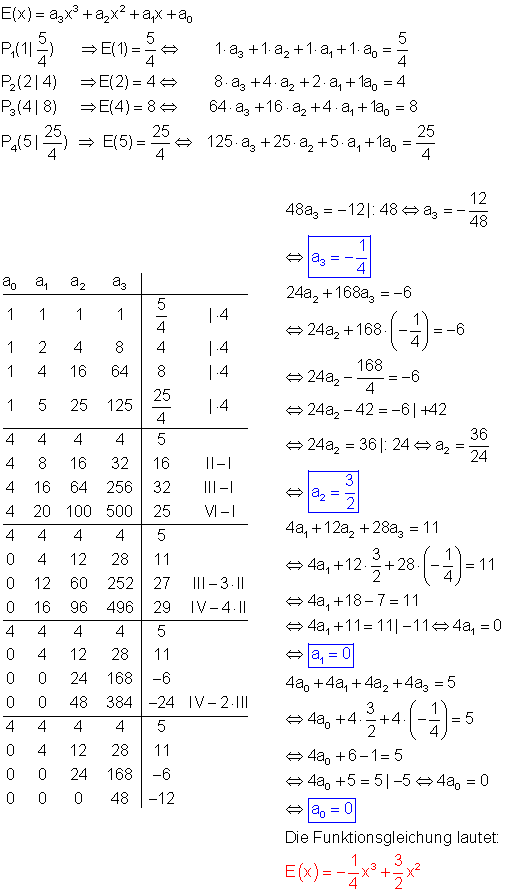
b) Funktionswerte für x = 3 ; und 7
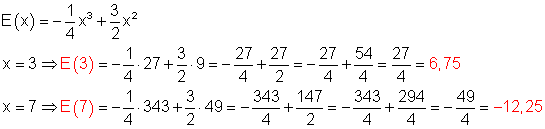
c) Für welchen Dosiswert ist die Effizienz der Bestrahlung am größten?
Gesucht ist die maximale Effizienz in Abhängigkeit von der Dosis. Die maximale Effizienz entspricht dem Maximum von E(x).

Für einen Dosiswert von x = 4 ist die Effizienz der Bestrahlung am größten.
d) Bei welcher Dosis ist die Effizienzzunahme am größten?
Da die Steigung des Graphen von E(x) ein Maß für die Effizienzzunahme ist, wird die Stelle gesucht, an der die Steigung des Graphen am größten ist. Die Stelle entspricht dem Dosiswert der größten Effizienzzunahme. Gesucht ist also die Wendestelle, denn dort nimmt die Steigung des Graphen einen Extremwert an.
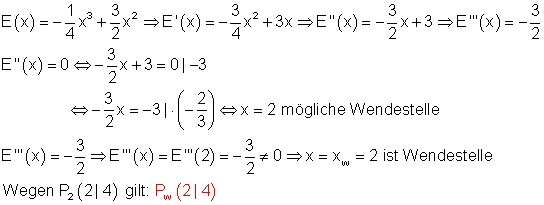
Bei einen Dosiswert von x = 2 ist die Effizienzzunahme der Bestrahlung am größten.
e) Bestimme die Achsenschnittpunkte.
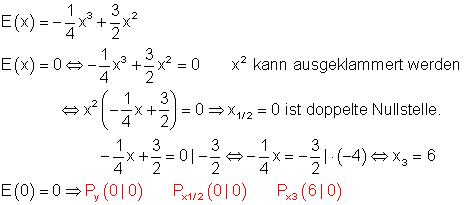
f) Trage alle bisher bekannten Werte in eine Wertetabelle ein.
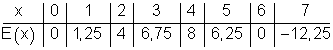
g) Zeichne den Graphen in ein geeignetes Koordinatensystem.
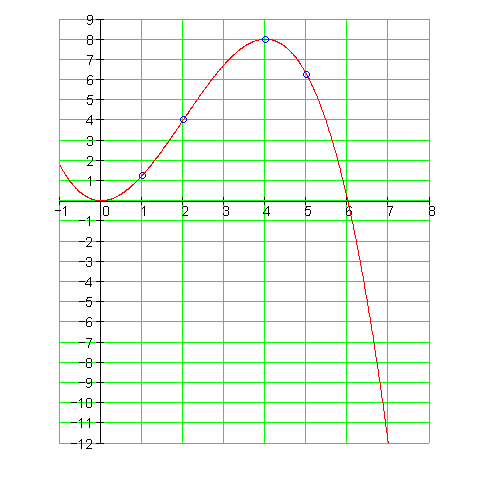
h) P1 ( 0 | 0 ) Wenn keine Bestrahlung erfolgt, ist keine Effizienz zu verzeichnen.
PMax ( 4 | 8 ) Bei der Dosis x = 4 ist die Effizienz der Bestrahlung am größten. Wird die Dosis erhöht, so sinkt die Effizienz, da verstärkt schädigende Wirkungen auftreten.
Pw ( 2 | 4 ) Bei einer Dosis von x = 2 ist die Effizienzzunahme am größten. Dort bewirken geringste Dosisverstärkungen eine große Effizienzzunahme.
P4 ( 6 | 0 ) Bei der Dosis x = 6 ist die Effizienz gleich Null. Die Nutzwirkung wird durch die schädigende Wirkung aufgehoben. Für x > 6 sind die schädigenden Strahlenwirkungen größer als der Nutzeffekt.
Möglicherweise würde der behandelnde Arzt sich für eine Dosis im Bereich 2 < x < 4 entscheiden. Dabei muss der Arzt sicherlich noch weitere Faktoren, die den Patienten betreffen berücksichtigen.
3.
Anwendungsaufgabe aus der Labortechnik (Chemie)
Bei einer chemischen Reaktion wird die Reaktionsstärke R auf einen Katalysator in Abhängigkeit von der Menge x durch Funktionen dritten Grades R(x) beschrieben. Die Reaktionsgeschwindigkeit des Prozesses wird als Ableitung R'(x) definiert. Eine Testreihe ergab bei einer Menge von x = 0 Mengeneinheiten (ME) die Reaktionsstärke R(0) = 0 Reaktionseinheiten (RE), bei x = 4 R(4) = 4, bei x = 8 R(8) = 8 und bei x = 12 R(12) = 0.
Ausführliche Lösung:
a) Bestimme die Funktion R(x) in Abhängigkeit von der Dosis x!

b) Für welche Menge x ist die Reaktion am stärksten?
Gesucht ist die maximale Reaktionsstärke in Abhängigkeit von der Dosis.Die maximale Reaktionsstärke entspricht dem Maximum von R(x).
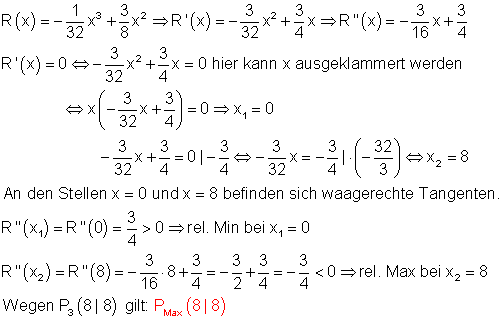
Für die Menge x = 8 ist die Reaktion am stärksten.
c) Bestimme den Wendepunkt.
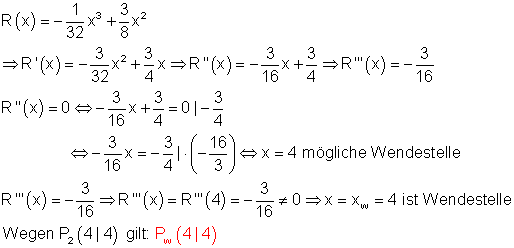
d) Bestimme die Funktionswerte für x = 2 ; 6 ; 10 ; 13 und stelle den Sachverhalt grafisch dar.
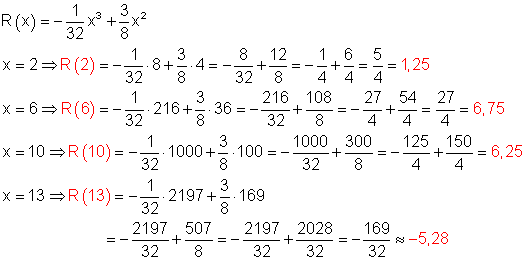
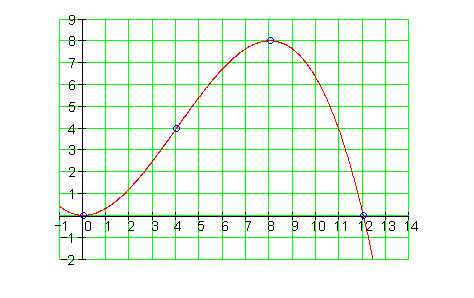
e) P1 ( 0 | 0 ) Ohne Katalysator läuft der Prozess nicht ab. Es ist keine Reaktion zu verzeichnen.
PMax ( 8 | 8 ) Bei einer Menge von x = 8 ist die chemische Reaktion am stärksten. Größere Mengen der Katalysatorsubstanz verringern die Reaktionsstärke.
P4 ( 12 | 0 ) Bei der Menge x = 12 findet keine Reaktion mehr statt. Die Für x > 12 ist die Reaktion ebenfalls Null.
Möglicherweise würde der Laborant, um die größtmögliche Reaktion zu erreichen eine Katalysatormenge von x = 8 zugeben.
Hier findest du die Aufgaben.
Und hier die Theorie hierzu: Kurvendiskussion mit Beispielen.
Hier findest du eine Übersicht über alle Beiträge zum Thema Differentialrechnung, darin auch Links zu weiteren Aufgaben.

