In diesem Beitrag findest du die Lösungen der Aufgaben zum freien Fall, unter anderem:
Wenn ein Stein in einen Brunnen fällt und man den Aufschlag nach 2 Sekunden hört, wie tief ist er?
Und: Aus welcher höhe müsste ein Auto frei fallen damit es 50 km/h erreicht?
1.
Aus welcher Höhe müsste ein Stein frei fallen, damit er unter Vernachlässigung des Luftwiderstandes die Schallgeschwindigkeit (v = 340 m/s) erreicht?
Ausführliche Lösung
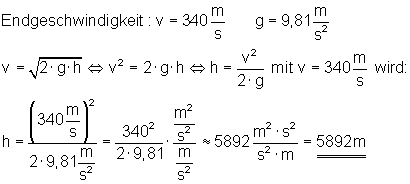
Der Stein müsste aus einer Höhe von etwa 5892 m fallen.
2.
Wir betrachten einen frei fallenden Körper ohne Luftwiderstand.
a)Nach welcher Zeit hat er die Geschwindigkeit v = 25 m/s erreicht?
b)Nach welcher Zeit hat er den Fallweg s = 10 m zurückgelegt?
c)Welche Werte findet man nach der jeweils doppelten Zeit?
d)Was gilt jeweils auf dem Mond ( gmond = 1,62 m/s2 )
Ausführliche Lösung
a) Der fallende Körper hat nach etwa 2,548 s die Geschwindigkeit v = 25 m/s.
b)
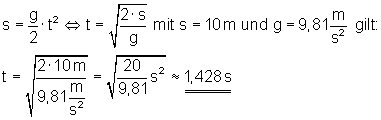
Der fallende Körper hat nach etwa 1,428 s einen Fallweg von 10 m zurückgelegt.
c)
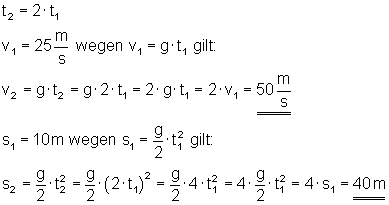
Nach der doppelten Zeit hat sich die Geschwindigkeit auf 50 m/s verdoppelt.
Nach der doppelten Zeit hat sich der Fallweg auf 40 m vervierfacht.
d)Auf dem Mond
a) Auf dem Mond hat der fallende Körper nach etwa 15,432 s die Geschwindigkeit v = 25 m/s erreicht.
b)
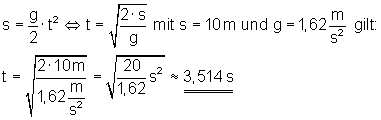
Auf dem Mond hat der fallende Körper nach etwa 3,514 s einen Fallweg von 10 m zurückgelegt.
c)
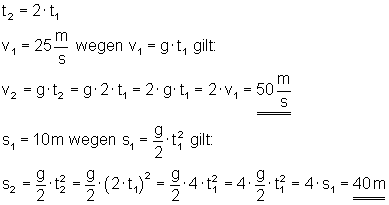
Auch auf dem Mond gilt:
Nach der doppelten Zeit hat sich die Geschwindigkeit auf 50 m/s verdoppelt.
Nach der doppelten Zeit hat sich der Fallweg auf 40 m vervierfacht.
3. Aus welcher Höhe müsste ein Auto frei fallen, damit es 50 km/h erreicht?
Ausführliche Lösung
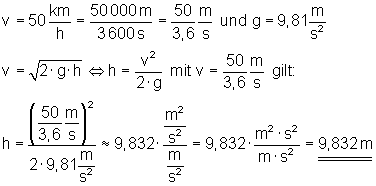
Das Auto müsste aus einer Höhe von etwa 9,832 m fallen um mit einer Geschwindigkeit von v = 50 km/h aufzuschlagen.
4. Stein fällt in Brunnen, wie tief?
Wenn ein Stein in einen Brunnen fällt und man den Aufschlag nach 2 Sekunden hört, wie tief ist er? Berücksichtige bei der Rechnung, dass der Schall 340 m/s zurücklegt.
Ausführliche Lösung
Gegeben: Zeit t = 2s , Schallgeschwindigkeit v = 340 \frac{m}{s} ; g = 9,81 \frac{m}{s^2} .
Das ist die Zeit, bis man den Aufschlag des Steins hört. Dabei müssen wir beachten, dass sie sich aus zwei Zeiteinheiten zusammensetzt:
t_f : Die Zeit, bis der Stein im Wasser landet, also die Fallbewegung. Für sie gilt: h = \frac{g}{2} \cdot t_f^2 .
t_s : Die Zeit, bis wir ihn hören, also die Schallgeschwindigkeit. Für sie gilt: h = v \cdot t_s .
Die gemessene Zeit setzt sich zusammen aus t = t_f + t_s = 2s . Deshalb können wir beide Gleichungen zusammensetzen:
\frac{g}{2} \cdot t_f^2 = v \cdot t_s
Aus t = t_f + t_s folgt t_s = t - t_f also:
\frac{g}{2} \cdot t_f^2 = v(t - t_f) = v \cdot t - v \cdot t_f \\
\Rightarrow \frac{g}{2} \cdot t_f^2 + v \cdot t_f - v \cdot t = 0
Somit haben wir eine quadratische Gleichung, die wir auf die Normalform bringen können:
t_f^2 + \frac{2 \cdot v}{g} \cdot t_f - \frac{2 \cdot v \cdot t}{g} = 0
Dies lösen wir mit der p-q-Formel:
p = \frac{2 \cdot v}{g} ; q = - \frac{2 \cdot v \cdot t}{g} \\
\Rightarrow D = (\frac{p}{2})^2 - q = (\frac{v}{g})^2 + \frac{2 \cdot v \cdot t}{g}
t_{f1/2} = - \frac{p}{2} \pm \sqrt D
\Rightarrow 1.: -\frac{v}{g} + \sqrt { (\frac{v}{g})^2 + \frac{2 \cdot v \cdot t}{g} } \\
\Rightarrow 2.: -\frac{v}{g} - \sqrt { (\frac{v}{g})^2 + \frac{2 \cdot v \cdot t}{g} } < 0 \Rightarrow Dies ergibt also keine Lösung.
Jetzt können wir unsere Werte einsetzen:
t_f = -\frac{v}{g} + \sqrt { (\frac{v}{g})^2 + \frac{2 \cdot v \cdot t}{g} }
= - \dfrac{340 \frac{m}{s}}{9,81 \frac{m}{s^2}} + \sqrt{(\dfrac{340 \frac{m}{s}}{9,81 \frac{m}{s^2}})^2 + \dfrac{2 \cdot 340 \frac{m}{s} \cdot 2s}{ 9,81 \frac{m}{s^2}} }
= -\frac{340}{9,81} s + \sqrt{ (\frac{340}{9,81})^2 s^2 + \frac{4 \cdot 340}{9,81} s^2} \approx 1,945401753 s
Mit der Formel für die Höhe ergibt sich daraus:
h = \frac{g}{2} \cdot t_f^2 = \frac{9,81}{2} \frac{m}{s} \cdot t_f^2 \approx \underline{\underline{18,65 m}}
Kontrollrechnung:
t_s = t - t_f = 2s - t_f \approx 0,054598247 s
Mit unserer 2. Formel für den Schall ergibt sich daraus:
\Rightarrow h = v \cdot t_s = 340 \frac{m}{s} \cdot t_s \approx \underline{\underline{18,56 m}}
Wenn ein Stein in einen Brunnen fällt und man den Aufschlag nach 2 Sekunden hört, dann ist der Brunnen also 18,56 Meter tief. Würde man die Zeit, die der Schall für den Weg nach oben benötigt, nicht berücksichtigen, dann wäre der Brunnen
h = \frac{9,81}{2} \frac{m}{s} \cdot 4 s^2 = 19,52 m tief. Die Abweichung beträgt also etwa 5,7 %.
5.
Fallschirmspringer landen mit einer Geschwindigkeit von etwa 20 km/h. Aus welcher Höhe müssen sich Fallschirmspringer ohne Fallschirm fallen lassen um eine solche Landung zu üben?
Ausführliche Lösung
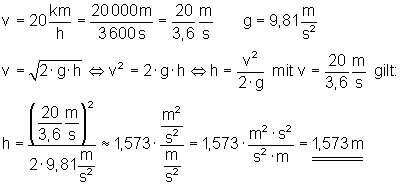
Um die Geschwindigkeit 20 km/h zu erreichen, müsste der Fallschirmspringeraus einer Höhe von etwa 1,573 m herunterspringen.
6.
Galilei hat angeblich Fallversuche am Schiefen Turm von Pisa ausgeführt.
Der Turm ist 55 m hoch.
a)Wie lange dauert es, bis ein oben losgelassener Stein den Boden berührt?
b)Aus welcher Höhe wurde ein Stein losgelassen, der nach 2,5 s auf dem Boden aufschlägt?
Ausführliche Lösung
a)
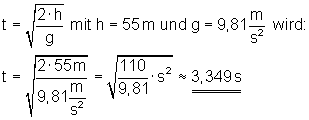
Bis zum Boden braucht der Stein etwa 3,349 s.
b)
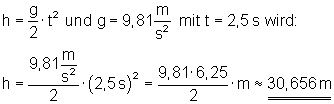
Der Stein wurde aus einer Höhe von etwa 30,656 m fallen gelassen.
7.
Um die Auswirkung von Auffahrunfällen zu demonstrieren, lässt eine Versicherung ein Auto aus 20 m Höhe frei zu Boden fallen. Mit welcher Geschwindigkeit in km/h müsste dasselbe Auto stattdessen gegen eine feste Wand fahren?
Ausführliche Lösung
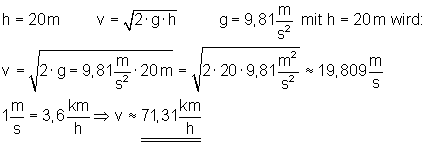
Das Auto müsste mit einer Geschwindigkeit von etwa 71,31 km/h gegen eine Wand fahren.
8.
Zwei verschieden große Stahlkugeln beginnen aus derselben Höhe gleichzeitig zu fallen. Kommen sie auch gleichzeitig am Boden an? Begründe es!
Ausführliche Lösung
Wird der Luftwiderstand nicht berücksichtigt, kommen beide Kugeln gleichzeitig unten an, da alle Körper gleich schnell fallen. Ansonsten wäre die kleine Kugel eher unten, weil sie der Luft weniger Widerstand bietet.
9.
Zwei Äpfel hängen im Abstand von 1,25 m übereinander an einem Baum.
a)Beide Äpfel fallen gleichzeitig. Verändert sich ihr Abstand beim Fallen?
b)Der untere Apfel beginne nun genau dann zu fallen, wenn der obere an ihm vorbeifliegt. Fallen sie ständig nebeneinander?
Ausführliche Lösungen
a)Der Abstand verändert sich nicht, da zu jedem Zeitpunkt die Geschwindigkeit beider Äpfel gleich ist.
b)Der obere überholt den unteren, da er bei Erreichen des Apfels schon eine Geschwindigkeit hat, die sich weiterhin erhöht.
10.
Der Raketenmotor eines Raumschiffs wirbelt beim Landen auf dem Mond sehr viel Staub auf. Warum ist nach dem Abstellen des Motors die Sicht sofort wieder klar, im Gegensatz zur Landung auf der staubigen Erdoberfläche?
Ausführliche Lösung
Auf dem Mond gibt es keine Atmosphäre, so dass der Staub sofort herunterfällt.
Hier findest du die Aufgaben.
Und hier die Theorie dazu Der freie Fall ohne Luftwiderstand.
Hier außerdem eine Übersicht über weitere Beiträge zum Thema Mechanik und Elektronik, darin auch Links zu Aufgaben.

