In diesem Beitrag erkläre ich Operationen mit Matrizen mit dem Casio fx-CG20 und Casio fx-CG50. Zuerst wiederhole ich zuerst die Matrizenaddition und Multiplikation. Danach zeige ich anhand von Beispielen die inverse Matrix, die Lösung einer Matrizengleichung mittels inverser Matrix, die transponierte Matrix, die Determinante einer Matrix, die Stufenform einer Matrix, das Quadrieren und Potenzieren einer Matrix und das Eingeben einer Einheitsmatrix.
Casio fx-CG20 auf Casio fx-CG50 updaten
Hier habe ich die Eingabe von Matrizen in den Matrizeneditor ([MENU] 1 {MAT/VCT}) erklärt.
Kurzwiederholung der Matrizenaddition und Multiplikation
Man kann nur Matrizen gleicher Dimension addierten oder subtrahieren.
Zur Berechnung gibt man zwei Matrizen A und B in den Matrix-Editor ein.
Die Eingabesequenz in der Hauptanwendung [MENU] 1 für die Addition beider Matrizen lautet:[OPTN] {MAT/VCT} {Mat} A[A] [+] {Mat} A[B] [EXE] .
Auf dem Display der Hauptanwendung erscheint danach:
Mat A+Mat B und das Additionsergebnis beider Matrizen.
Für die Subtraktion gibt man lediglich statt [+] [-] ein.
Eine Matrix A kann man nur dann mit einer Matrix B multiplizieren, wenn die Anzahl der Spalten von A mit der Anzahl der Zeilen von B übereinstimmt.
Die Eingabesequenz in der Hauptanwendung [MENU] 1 für die Multiplikation beider Matrizen lautet:
[OPTN] {MAT/VCT} {Mat} A[A] [x] {Mat} A[B] [EXE]
Auf dem Display der Hauptanwendung erscheint danach:
Mat AxMat B und das Multiplikationsergebnis beider Matrizen.
Man kann die Matrizenmultiplikation nicht umkehren.
Die inverse Matrix
Für die Matrix A suchen wir eine Matrix X, für die gilt:
![]()
Wobei E die Einheitsmatrix ist, die in der Diagonalen nur aus der Zahl 1 besteht, deren andere Werte 0 sind.
Kann man eine solche Matrix X finden, so nennt man sie die inverse Matrix zu A und bezeichnet diese mit A -1
Zur Matrix suchen wir
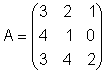
die inverse Matrix und machen anschließend die Probe.
Nachdem wir die Matrix A eingegeben haben, wird sie inversiert:

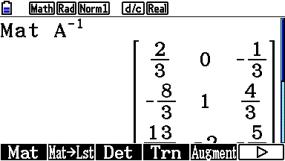 .
.
Für die Inverse A-1 von A muss gelten:
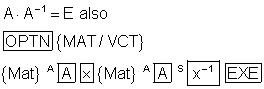
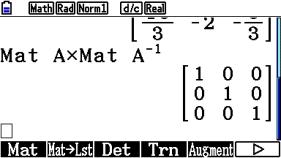
Inverse Matrizen gibt es nur für quadratische Matrizen.
Lösung einer Matrizengleichung mittels inverser Matrix
Wir wollen als nächstes folgende Matrizengleichung lösen:
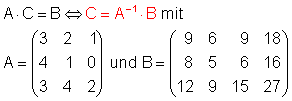
A und B werden in den Matrix-Editor eingegeben.
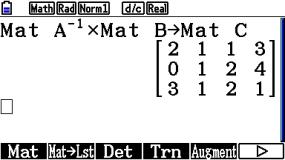
Zuletzt machen wir die Probe mit [OPTN] {MAT/VCT} {Mat} A[A] [x] {Mat} A[C] [EXE].
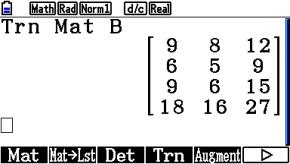
Transponierte Matrix
Wenn wir Zeilen und Spalten vertauschen, entsteht eine transponierte Matrix.
Wir wollen folgende Matrix transponieren:
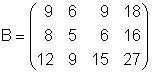
Wir geben die Matrix B in den Matrix-Editor ein.
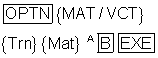
Anwendung Skalarprodukt
Wir wollen das Skalarprodukt zweier Vektoren bilden.
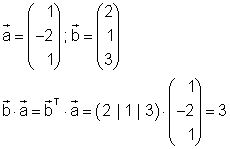
Wir geben beide Vektoren als Matrix A und B ein.
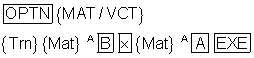
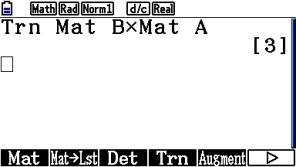
Die Determinante einer Matrix
Man kann Determinanten nur für quadratische Matrizen berechnen.
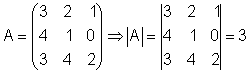
Wir geben die Matrix A ein.

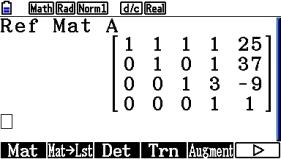
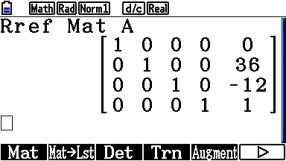
Stufenform einer Matrix
Wenn wir ein lineares Gleichungssystem mit dem Gauß-Algorithmus lösen wollen, so können wir das mit der Stufenform einer Matrix machen.
Die Matrix A entspricht dabei der eines linearen Gleichungssystems mit vier Gleichungen und vier Unbekannten.
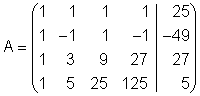
Wir geben die Matrix A ein.
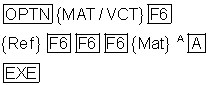
Diagonalisieren einer Matrix
Wenn wir ein lineares Gleichungssystem mit dem Gauß-Algorithmus lösen wollen, so könen wir das mit der Diagonalisierung einer Matrix machen.
Die Matrix A entspricht dabei der eines linearen Gleichungssystems mit vier Gleichungen und vier Unbekannten.
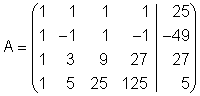
Wir geben die Matrix A ein.
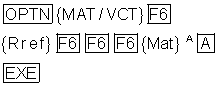
Quadrieren und potenzieren einer Matrix
Man kann nur quadratische Matrizen quadrieren oder potenzieren.
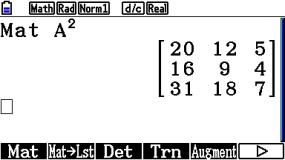
Das quadrieren der Matrix A ergibt:
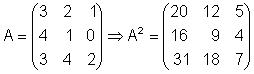
Wir geben die Matrix A ein.

Wenn wir die Matrix potenzieren wollen, so müssen wir statt x2 die Potenz eingeben.
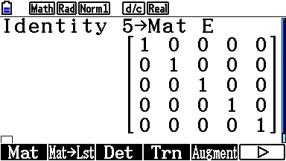
Eingeben einer Einheitsmatrix
Wir wollen eine 5×5 Einheitsmatrix unter dem Namen Mat E eingeben.
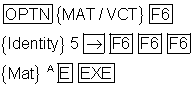
Weitere Beispiele zu dem Casio fx-CG20 findest du in der Kategorie GTR.
Außerdem in der Übersicht über alle Beiträge zum grafikfähigen Taschenrechner Casio fx-CG20.


