In diesem Beitrag zeige ich zuerst, wie man mit den grafikfähigen Taschenrechnern Casio fx-CG20 und Casio fx-CG 50 eine Matrix eingibt, editiert, löscht. Danach erkläre ich anhand von Beispielen die Rechnungen mit Matrizen: Matrizenaddition, Matrizensubtraktion und Matrizenmultiplikation. Anschließend die Multiplikation einer Matrix mit einer Zahl. Zuletzt die Skalarmultiplikation zweier Vektoren.
Casio fx-CG20 auf Casio fx-CG50 updaten
Matrix eingeben
Zuerst müssen wir die Dimension der Matrix festlegen.
Im folgendem zeige ich dies am Beispiel, einer 4 x 3 – Matrix.
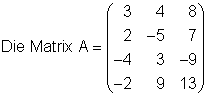 .
.
Die Befehlsfolge [MENU] 1 {MAT/VCT} öffnet den Matrixeditor.
Der Cursor steht danach auf Mat A.
Das bedeutet, die einzugebende Matrix erhält den Namen A, bzw. deren Daten werden in der Variablen A gespeichert.

Mit [EXE] 4 [EXE] 3 [EXE]
geben wir die Dimension der Matrix ein.
m steht dabei für Zeile, n steht für Spalte.
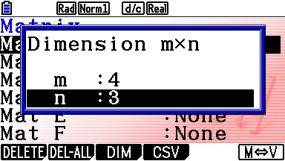
[EXE] öffnet das Eingabefenster. Jetzt können wir die Zahlenwerte eingeben.
Die Eingabesequenz obiger Matrix lautet:
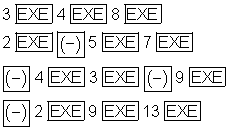
Wir beenden die Eingabe mit [EXIT] [EXIT]
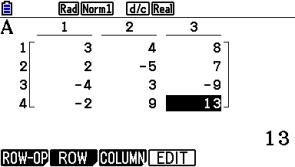
Damit gelangt man wieder in den Rechenbildschirm.
Jetzt kann man die Matrix bearbeiten oder mit ihr rechnen.
Matrix editieren, Matrix löschen
Mit [MENU] 1 {MAT/VCT} [EXE] kann man die im Matrix-Editor selektierte Matrix aufrufen.
Wenn man einen bestimmten Matrixwert ändern will, dann bewegt man den Cursor an die betreffende Stelle, überschreibt den alten Wert mit dem neuen und quittiert mit [EXE].
Mit [EXIT] gelangt man zurück in den Matrix-Editor.
Soll eine bestimmte Matrix gelöscht werden, so selektiert man sie mit dem Cursor.
{DELETE} [F1] löscht die ausgewählte Matrix,
{DELETE} [F6] bricht den Löschvorgang ab.
{DEL_ALL} [F1] löscht alle Matrizen,
{ DEL_ALL } [F6] bricht den Löschvorgang ab.
Matrizenaddition und Subtraktion
Man kann nur Matrizen gleicher Dimension addieren oder subtrahieren.
Zur Berechnung gibt man zwei Matrizen A und B in den Matrix-Editor ein.
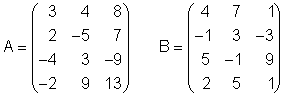
Mit [EXIT] [EXIT] gelangt man nach der Eingabe in die Hauptanwendung (Run-Matrix).
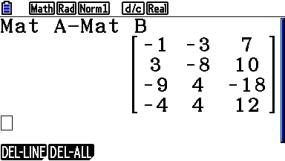
Addition der Matrizen A und B:
Die Eingabesequenz für die Addition beider Matrizen lautet:
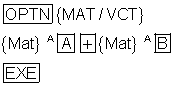
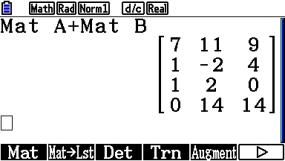
Subtraktion der Matrizen A und B:
Die Eingabesequenz für die Subtraktion beider Matrizen lautet:
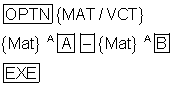
Matrizenmultiplikation
Eine Matrix A kann nur dann mit einer Matrix B multipliziert werden, wenn die Anzahl der Spalten von A mit der Anzahl der Zeilen von B übereinstimmt.
Zur Berechnung gibt man zwei Matrizen A und B in den Matrix-Editor ein.
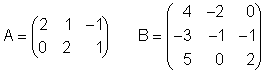
Mit [EXIT] [EXIT] gelangt man nach der Eingabe in die Hauptanwendung (Run-Matrix).
Die Eingabesequenz für die Multiplikation beider Matrizen lautet:
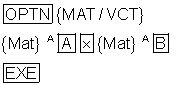
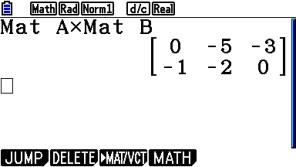
Für die Multiplikation zweier Matizen gilt:
Die Matrix C hat die Zeilenzahl m von A und die Spaltenzahl p von B.
![]() .
.
Multiplikation einer Matrix mit einer Zahl
Will man eine Matrix mit einer Zahl multiplizieren, so muss man jedes Element der Matrix mit dieser Zahl multiplizieren.
Diese Multiplikation kann ebenfalls durch eine Matrixmultiplikation erfolgen.
Wir wollen die Matrix B mit der Zahl -1 multiplizieren.
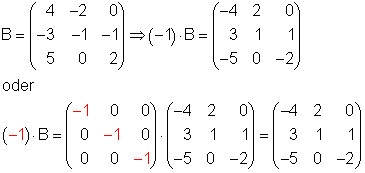
Wir geben beide Matrizen in den Matrizeneditor, danach multiplizieren wir so:
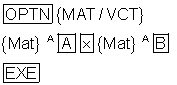
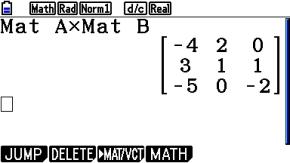
Die erste Matrix A ist eine Diagonalmatrix. Mit anderen Worten ein quadratische Matrix, die nur in der Diagonalen Werte ungleich Null enthält.
Sie hat soviel Spalten, wie die zweite Matrix B Zeilen hat. In der Diagonalen steht dabei die Zahl, mit der die zweite Matrix zu multiplizieren ist.
Ein viel einfacher Weg ist, die Matrix B direkt mit der Zahl zu multiplizieren und das Ergebnis in Mat C zu kopieren.
[OPTN] {MAT/VCT} {Mat}
A[B] [x] [ ( ] [(-)] 1 [ ) ]
[→] {Mat} A[C] [EXE]Mat Bx (-1) → Mat C
Skalarmultiplikation zweier Vektoren
Vektoren kann man als einzeilige oder einspaltige Matrizen auffassen.
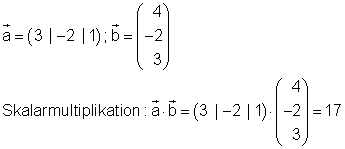
Nachdem man Zeilenvektor A (Dimension 1×3) und Spaltenvektor B (Dimension 3×1) als Matrizen in den Matrizeneditor eingegeben hat, berechnet man so:
[OPTN] {MAT/VCT} {Mat} A [A] [x] {Mat} A [B] [EXE].
Weitere Beispiele zu dem Casio fx-CG20 findest du in der Kategorie GTR.
Außerdem in der Übersicht über alle Beiträge zum grafikfähigen Taschenrechner Casio fx-CG20.


