Hier findest du die Lösungen der Dreisatz Aufgaben II mit komplettem Lösungsweg.
In diesem 
Video Einfacher Dreisatz erkläre ich leicht verständlich, wie man Dreisatzaufgaben ganz einfach löst.
1. Ein Getränkemarkt
verkauft für ein Fest 65 Kisten Fanta für 520 Euro.
Wie viel muss man für 87 Kisten zahlen, wenn es keinen Rabatt gibt?
Überlegung: Wir wissen: 65 Kisten Fanta kosten 520 €.
Die gesuchte Größe ist der Preis für 87 Kisten Fanta.
Wir müssen also als erstes ausrechen, was eine Kiste kostet.
Beim Dreisatz geht man stets in drei Schritten (Sätzen) vor:
1. Satz: Bekanntes Verhältnis: 65 Kisten kosten 520 Euro.
2. Satz: Schluss auf die Einheit: Eine Kiste kostet den 65. Teil.
3. Satz: Schluss auf die gesuchte Mehrheit: 87 Kisten kosten 87 mal soviel.
Daraus entsteht zur Rechnung ein Bruch, bei dem der Ausgangswert (hier 520 Euro) im Zähler steht.
Teil steht im Nenner (hier 65),
mal steht im Zähler (hier 87).
Zuvor sollte man sich immer überlegen, welche Größe gesucht wird und ob die Zuordnung proportional oder antiproportional ist.
Lösung: Für 87 Kisten Fanta muss man 696 Euro zahlen.
2. 7 Arbeiter
heben einen Graben in 5 Tagen aus.
Wie lange würden 10 Arbeiter brauchen?
Überlegung: Die gesuchte Größe ist die Zeit, die 10 Arbeiter brauchen.
Lösung: 10 Arbeiter würden für den Graben 3,5 Tage brauchen.
In diesem Video Einfacher Dreisatz erkläre ich leicht verständlich eine ganz ähnliche Aufgabe.
3. Eine Maschine
fertigt in 30 Minuten 2500 Schrauben.
Wie lange braucht sie für 1500 Schrauben?
Überlegung: Die gesuchte Größe ist die Zeit, die die Maschine für die Herstellung von 1500 Schrauben benötigt.
Zur Herstellung von 1500 Schrauben benötigt die Maschine 18 Minuten.
4. Der Futtervorrat
reicht für 5 Pferde 240 Tage.
Für wie viele Pferde würde er 80 Tage reichen?
Überlegung: Die gesuchte Größe ist die Anzahl der Pferde, für die der Futtervorrat 80 Tage reichen würde.
Lösung: Für 15 Pferde würde der Futtervorrat 80 Tage reichen.
5. In einem Zeltlager
kauft man für 30 Jugendliche für die nächsten 10 Tage 60 kg Nudeln.
Um wie viel Tage kann man die Freizeit verlängern, wenn fünf Jugendliche weniger erscheinen und insgesamt 80 kg Nudeln vorhanden sind?
Überlegung: Die gesuchte Größe ist die Anzahl der Tage, die 25 Schüler mit 80 kg Nudeln auskommen.
Bei dieser Aufgabe handelt es sich um einen verschachtelten Dreisatz.
Zuerst erfolgt der Schluss von 30 Schüler auf 25 Schüler (antiproportional).
Danach der Schluss von 60 kg Nudeln auf 80 kg (proportional).
Dabei ist es wichtig, die Reihenfolge einzuhalten und nicht zwei Größen gleichzeitig zu verändern.
Man kann den Dreisatz auch verkürzt darstellen, solange der Zusammenhang der Größen dabei einsichtig ist.
Lösung: 25 Schüler kommen mit 80 kg Nudeln 16 Tage aus. Damit kann die Freizeit um 6 Tage verlängert werden
6. Ein 5 m2 großes Kupferblech,
3 mm dick, wiegt 133,8 kg.
Wie viel wiegt ein 2 mm dickes Kupferblech, das eine Fläche von 3 m2 hat?
Überlegung: Die gesuchte Größe ist das Gewicht eines Kupferbleches mit der Fläche 3 m2 und einer Dicke von 2 mm.
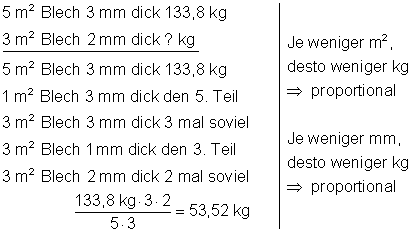
Lösung: Das Kupferblech wiegt 53,52 kg.
Dazu kannst du dir das Video antiproportionaler Dreisatz ansehen. Darin erkläre ich leicht verständlich eine ähnliche Aufgabe mit einem doppelten Dreisatz.
7. Ein Wassertank
wird durch 3 gleiche Leitungen in 6 Stunden gefüllt, wenn jede stündlich 500 Liter Wasser liefert.
Wie lange würde man mit 4 Leitungen brauchen, wenn jede stündlich nur 300 Liter Wasser liefert?
Überlegung: Die gesuchte Größe ist die Zeit, in der mit 4 Leitungen, die jede stündlich 300 Liter Wasser liefern, das Becken gefüllt werden kann.
Lösung: 4 Leitungen mit 300 Liter/h füllen den Wassertank in 7,5 Stunden.
8. Eine 80 m lange Mauer
wird von 3 Arbeitern in 6 Tagen hochgezogen, wenn sie täglich 8 Stunden arbeiten.
Wie viel Arbeiter benötigt man, um eine 140 m lange Mauer in 7 Tagen hochzuziehen, wenn die tägliche Arbeitszeit auf 9 Stunden erhöht wird?
Überlegung: Die gesuchte Größe ist die Anzahl der Arbeiter, die eine 140 m lange Mauer in 7 Tagen bei einer täglichen Arbeitszeit von 9 Stunden hochziehen.
Bei dieser Aufgabe handelt es sich um einen zweifach verschachtelten Dreisatz.
Zuerst erfolgt der Schluss von 80 m auf 140 m Mauer (proportional).
Danach der Schluss von 8 h täglicher Arbeitszeit auf 9 h (antiproportional).
Zuletzt der Schluss von 6 Tage auf 7 Tage (antiproportional).
Lösung: Also werden 4 Arbeiter benötigt, um eine 140 m lange Mauer in 7 Tagen bei 9 Stunden täglicher Arbeitszeit hochzuziehen.
Hier findest du die Aufgaben.
Außerdem hier weitere Dreisatz-Aufgaben.
Außerdem kannst du den Wikipediaartikel zum Dreisatz lesen.
Und hier eine Übersicht über alle Beiträge zum Thema Dreisatz und zu anderen mathematischen Grundlagen.
