Hier findest du die Lösungen der Aufgaben zu lineare Funktionen II.
1. bis 4.:
Eine Gerade hat die Steigung a1 und verläuft durch den Punkt P. Bestimme die Funktionsgleichung f(x), die Achsenschnittpunkte und zeichne den Graphen!
Vorgehensweise:
In die allgemeine Form der Funktionsgleichung einer linearen Funktion trägt man den Steigungsfaktor a1 ein. Mit den Koordinaten des vorgegebenen Punktes lässt sich die Konstante a0 berechnen. Die y-Koordinate von Py lässt sich aus der Funktionsgleichung ablesen. Den Schnittpunkt mit der x-Achse findet man, indem die Funktionsgleichung Null gesetzt und nach x aufgelöst wird. Der so gefundene x-Wert ist die Nullstelle, an der der Graph die x-Achse schneidet. Mit den nun bekannten Punkten lässt sich der Graph zeichnen.
Dazu kannst du dir das Video 📽️Lineare Funktion und Umkehrfunktion zeichnen ansehen.
1.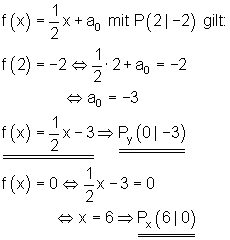
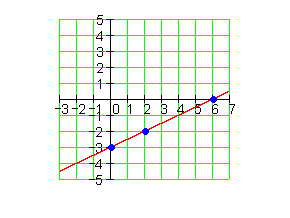
2.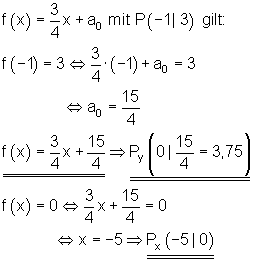
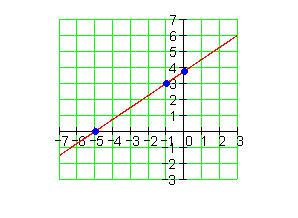
3.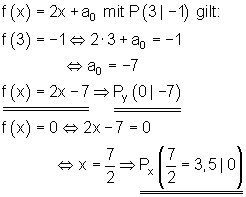
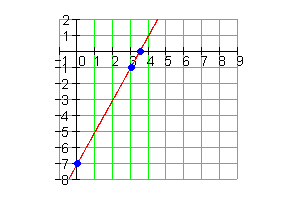
4.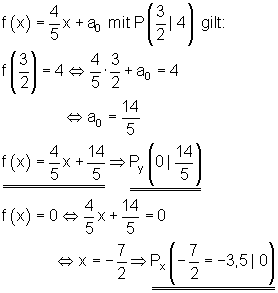
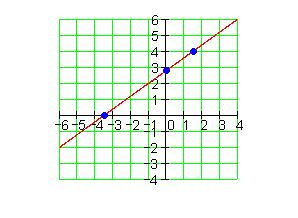
5. bis 10.:
Eine Gerade verläuft durch die Punkte P1 und P2. Bestimme die Funktionsgleichung f(x), die Achsenschnittpunkte und zeichne den Graphen!
Vorgehensweise:
Mit den Koordinaten der beiden vorgegebenen Punkte berechnet man den Steigungsfaktor a1 und trägt ihn in die allgemeine Form der Funktionsgleichung ein. Mit den Koordinaten eines der vorgegebenen Punkte lässt sich die Konstante a0 berechnen. Die y-Koordinate von Py lässt sich aus der Funktionsgleichung ablesen. Den Schnittpunkt mit der x-Achse findet man, indem die Funktionsgleichung Null gesetzt und nach x aufgelöst wird. Der so gefundene x-Wert ist die Nullstelle, an der der Graph die x-Achse schneidet. Verbindet man die in der Aufgabenstellung vorgegebenen Punkte im Koordinatensystem miteinander, so erhält man den Graphen der Funktion.
Dazu kannst du dir auch den zweiten Teil (ab der 3. Minute) dieses Videos ansehen:
5.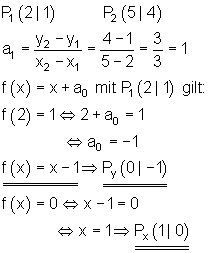
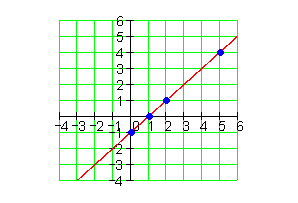
6.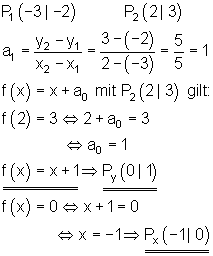
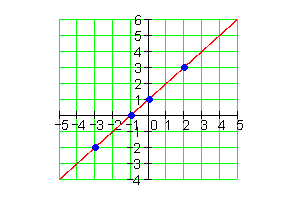
7.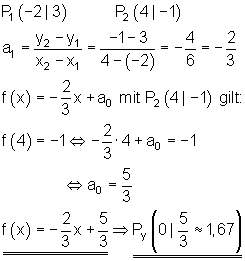
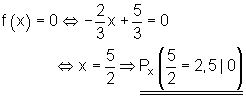
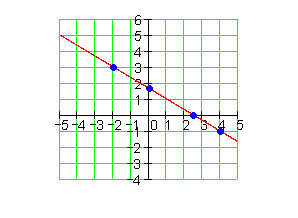
8.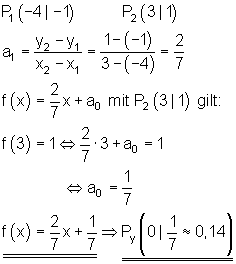
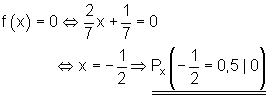
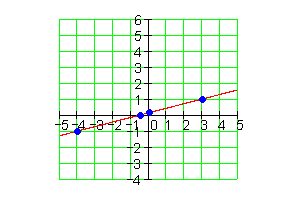
9.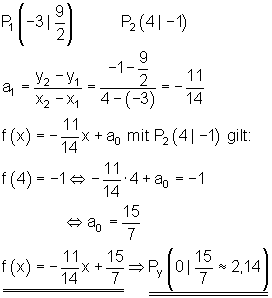
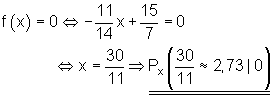
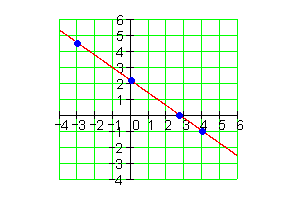
10.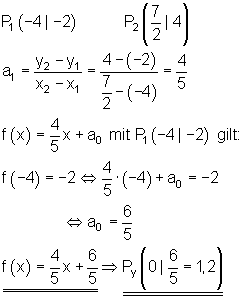
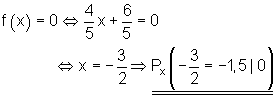
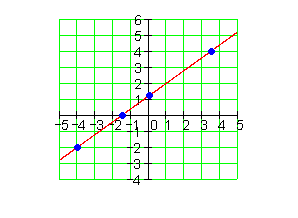
Hier sind die Aufgaben dazu.
Und hier die Theorie: Funktionsgleichungen aufstellen.
Hier finden Sie eine Übersicht über weitere Beiträge zu linearen Funktionen, dort auch Links zu weiteren Aufgaben.

