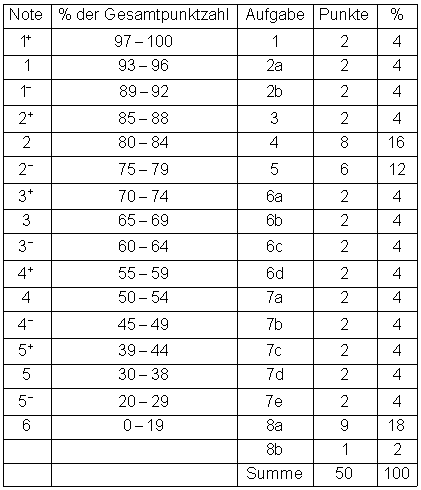
Hier findest du die Lösungen der Klassenarbeit zum Thema Stochastik I im Beruflichem Gymnasium Jahrgangsstufe 13 mit komplettem Lösungsweg.
1.
Ausführliche Lösung
Wählt man aus der Bevölkerung zufällig eine Person aus, so ist die Wahrscheinlichkeit 36,5%, dass diese Person die Blutgruppe 0 hat.
2.
Ausführliche Lösungen
a)
![]()
b) Die Chancen stehen 3:1
3.
Ausführliche Lösung
Urnenmodell:
Urne mit 8 Kugeln, 5 grüne (kein Schmuggler KS), 3 rote (Schmuggler S) Einmal ziehen.
Die Wahrscheinlichkeit einen Schmuggler zu erwischen beträgt:
![]()
4. Ausführliche Lösung
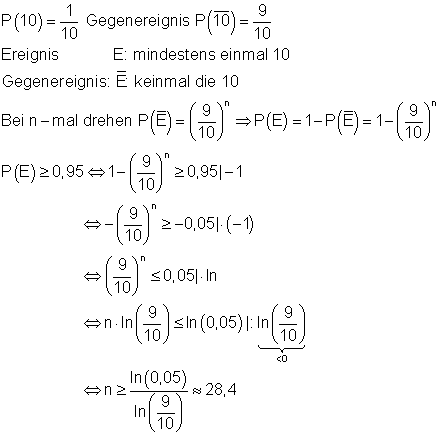
Man muss das Glücksrad mindestens 29 mal drehen, um mit einer Sicherheit von mindestens 95% mindestens einmal die 10 zu erhalten.
5. Ausführliche Lösung
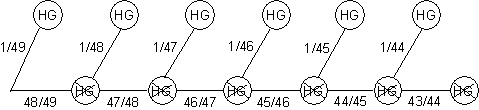
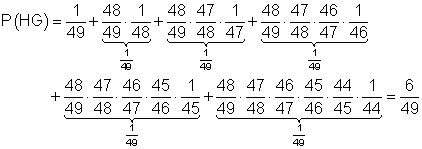
Die Wahrscheinlichkeit, dass der Hauptgewinn bei irgendeiner der 6 Ziehungen gezogen wird beträgt:
![]()
6. Ausführliche Lösungen
a)
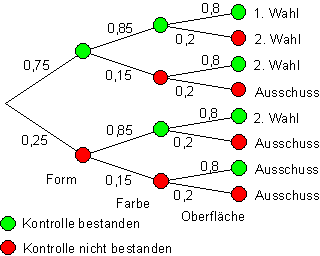
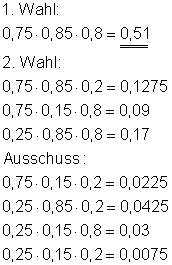
b)
Die Wahrscheinlichkeit dafür, dass ein Teil 1. Wahl ist, beträgt:
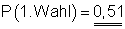
c)
Die Wahrscheinlichkeit dafür, dass ein Teil 2. Wahl ist, beträgt:
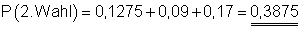
d)
Die Wahrscheinlichkeit dafür, dass ein Teil Ausschuss ist, beträgt:
![]()
7. Ausführliche Lösungen
a)
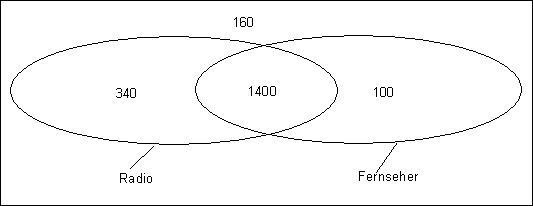
b)
In 1740 + 1500 – 1400 = 1840 Haushalten gibt es Radio oder Fernseher.
c)
Die Wahrscheinlichkeit dafür, das ein zufällig ausgewählter Haushalt Radio und Fernseher besitzt beträgt:
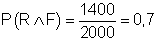
d)
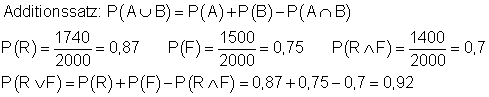
Die Wahrscheinlichkeit dafür, das ein zufällig ausgewählter Haushalt Radio oder Fernseher besitzt beträgt:
![]()
e)
Die Wahrscheinlichkeit dafür, das ein zufällig ausgewählter Haushalt weder Radio noch Fernseher besitzt beträgt:
![]()
8. Ausführliche Lösungen
a) Aufstellen der Vierfeldtafel mit den vorgegebenen Daten.
Die % Werte entsprechen relativen Häufigkeiten (Wahrscheinlichkeiten)
90 % Spam bedutet Summe Spam = 0,9
10% gute Mails bedeutet Summe gute Mails = 0,1
40% der Spam-Mails mit Viegro bedeutet 0,9 x 0,4 = 0,36
1% der guten Mails mit Viegro bedeutet =0,1 x 0,01 = 0,001
Die restliche Werte kann man ausrechnen, da die Summen bekannt sind.

Spam ohne Viegro: 0,9 – 0,36 = 0,54
Gute Mail ohne Viegro: 0,1 – 0,001 = 0,099
Summe aller Mails mit Viegro: 0,36 + 0,001 = 0,361
Summe aller Mails ohne Viegro: 0,54 + 0,099 = 0,639
Mit diesen Werten wird die Vierfeldtafel nun vervollständigt.

b)
![]()
Die Wahrscheinlichkeit, dass eine gute Mail das Wort „Viegro“ enthält beträgt 0,001.
Leistungsbewertung
Hier findest du die Aufgaben.
und hier eine Übersicht über alle Beiträge zur Wahrscheinlichkeitsrechnung, dort auch Links zu weiteren Aufgaben.