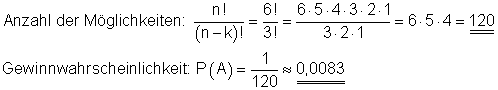Hier findest du die Lösungen der vermischten Aufgaben Stochastik I.
1.
Ein Würfel wird einmal geworfen.
Es werden zwei Ereignisse festgelegt:
A: Die Augenzahl ist größer als 4.
B: Die Augenzahl ist eine ungerade Zahl und größer als 1.
Ein neues Ereignis wird wie folgt festgelegt:
C: Die Augenzahl ist größer als 4 oder Die Augenzahl ist eine ungerade Zahl und größer als 1.
Das Ereignis C ist eine Oder-Verknüpfung aus A und B.
Bestimme die Wahrscheinlichkeit P(C).
Ausführliche Lösung
Zuerst bilden wir die Ereignismengen von A und B.
A = \{5;6\} \qquad B = \{3;5\}Nach der Summenregel ist nun P(C) = P(A \cup B) = P(A) + P(B) - P(A \cap B) zu berechnen.
Dazu benötigen wir noch die Ereignismenge von A \cap B. \qquad A \cap B = \{5\}
Die Wahrscheinlichkeiten der einzelnen Ereignisse sind:
P(A) = \dfrac{1}{6} + \dfrac{1}{6} = \dfrac{2}{6} = \dfrac{1}{3} \qquad P(B) = \dfrac{1}{6} + \dfrac{1}{6} = \dfrac{2}{6} = \dfrac{1}{3} \qquad P(A \cap B) = \dfrac{1}{6}Damit wird die Wahrscheinlichkeit von C:
P(A) = P(A \cup B) = P(A) + P(B) - P(A \cap B) = \dfrac{1}{3} + \dfrac{1}{3} - \dfrac{1}{6} = \dfrac{2}{6} + \dfrac{2}{6} - \dfrac{1}{6} = \dfrac{3}{6} = \underline{\underline{\dfrac{1}{2}}}
2.
Eine Karte wird aus einem Spiel mit 32 Karten gezogen (Skat).
Welche Wahrscheinlichkeit hat das folgende Ereignis?
E: Die gezogene Karte ist eine Bildkarte oder eine Kreuzkarte.
Ausführliche Lösung
Das Ereignis E ist eine Oder- Verknüpfung aus den Ereignissen
A: Die gesuchte Karte ist eine Bildkarte
B: Die gesuchte Karte ist eine Kreuzkarte.
Zuerst bestimmen wir die Anzahl der möglichen Ergebnisse von A und B.
A: Es gibt 12 Bildkarten von insgesamt 32 Karten.
B: Es gibt 8 Kreuzkarten von insgesamt 32 Karten.

Die Wahrscheinlichkeit dafür, dass die gezogene Karte eine Bild- oder eine Kreuzkarte ist beträgt etwa 0,53
3.
Ein Fahrradschloss (Zahlenschloss) besteht aus vier unabhängig voneinander beweglichen Rädern, die jeweils 6 Ziffern ( von 1 bis 6 ) enthalten.
Das Schloss öffnet sich nur bei einer ganz bestimmten Zahlenkombination.
Wie viele Stellungen (Zahlenkombinationen) hat das Fahrradschloss und wie groß ist die Wahrscheinlichkeit, bei der ersten Einstellung das Schloss zu öffnen?
Ausführliche Lösung
Modellierung mit dem Urnenmodell:
Eine Urne enthält n = 6 Kugeln mit den Nummern 1 bis 6.
Es wird k = 4 mal gezogen mit Zurücklegen.

4.
Aus den 26 Buchstaben des Alphabets werden nacheinander blind drei Buchstaben mit Zurücklegen entnommen.
Wie groß ist die Wahrscheinlichkeit dreimal denselben Buchstaben zu ziehen?
Ausführliche Lösung
Modellierung mit dem Urnenmodell:
Eine Urne enthält n = 26 Kugeln mit den Buchstaben A bis Z.
Es wird k = 3 mal gezogen mit Zurücklegen.

5.
In einer Lostrommel befinden sich 6 Lose mit den Nummern 1 bis 6.
Ein Spieler zieht nacheinander drei Lose. Zieht er in der Reihenfolgedie Nummern 2, 4 und 6, so hat er gewonnen.
Berechne die Wahrscheinlichkeit für einen Gewinn.
Ausführliche Lösung
Zuerst wird die Anzahl der Möglichkeiten berechnet, von diesen gibt es nur eine, die zum Gewinn führt, nämlich die Zahlenfolge 2, 4, 6. Es handelt sich um eine geordnete Stichprobe ohne Zurücklegen. Aus n = 6 Zahlen werden k = 3 Zahlen gezogen.
6.
Aus einem Kartenspiel mit 32 Karten werden 8 Karten gezogen.
Wie groß ist die Wahrscheinlichkeit dafür, dass dies 8 Karo- Karten sind?
Ausführliche Lösung
Die Wahrscheinlichkeit bei 8 Zügen jeweils Karo zu ziehen ist:

7.
Jedes Los gewinnt!
Bei der Abi- Abschlussfeier muss jeder der 50 Teilnehmer ein Los kaufen. Der 1. Preis hat einen Wert von 100 €, der 2. von 25 € und der 3. von 10 €. Jeder, der keinen dieser Gewinne bekommt, erhält einen Trostpreis in Höhe von 1 €.
Wie teuer müsste ein Los sein, damit Einnahmen und Ausgaben überein stimmen? Jedes Los wird für 5 € verkauft. Der Erlös geht ans Friedensdorf. Wie groß ist der Erlös?
Ausführliche Lösung:
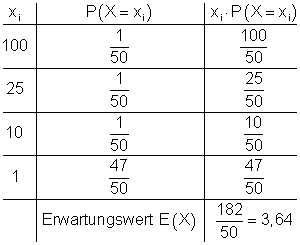
Der Erwartungswert wird berechnet:
E(X) = 3,64 bedeutet, dass jedes Los 3,65 € kosten muss, damit die Ausgaben gedeckt werden.
Bei einem Lospreis von 5 € und 50 verkauften Losenentsteht ein Gewinn von
![]()
Dieser Betrag geht ans Friedensdorf.
Hier findest du die Aufgaben.
Und hier eine Übersicht über alle Beiträge zur Wahrscheinlichkeitsrechnung, dort auch Links zu weiteren Aufgaben.