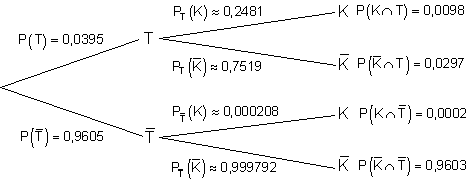Hier findest du die Lösungen zu weiteren Aufgaben zur bedingten Wahrscheinlichkeit.
1.
Es soll die Beliebtheit einer Fernsehsendung überprüft werden. Eine Blitzumfrage hatte folgendes Ergebnis:
30% der Zuschauer, die die Sendung gesehen hatten, waren 25 Jahre und jünger. Von diesen hatten 50% und von den übrigen Zuschauern (über 25 Jahre) hatten 80% eine positive Meinung.
a) Stelle den Sachzusammenhang in einer 4-Feldertafel da. Verwende die Ereignisse (mit ihren Gegenereignissen):
A: Der Zuschauer ist 25 Jahre alt und jünger.
B: Der Zuschauer hat eine positive Meinung über die Sendung.
b) Zeichne das Baumdiagramm und den inversen Baum.
Bestimmen Sie alle Pfadwahrscheinlichkeiten.
c) Wie viel % der Zuschauer, von denen man weiß, dass sie eine positive Meinung über die Sendung hatten, waren älter als 25 Jahre?
d) Wie viel % der Zuschauer, von denen man weiß, dass sie älter als 25 Jahre sind, hatten keine positive Meinung über die Sendung?
e) Überprüfe durch Rechnung ob das Ereignis B unabhängig vom Ereignis A ist.
1. Ausführliche Lösungen
a)

b) Das Baumdiagramm:
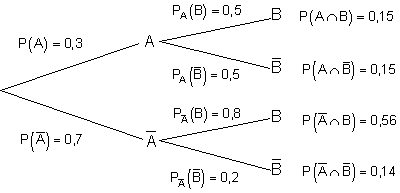
Berechnung aller für den Baum relevanten Wahrscheinlichkeiten.
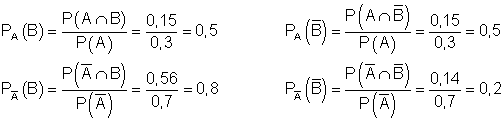
Der inverse Baum:
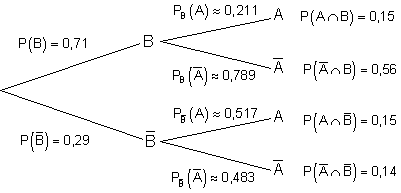
Berechnung aller für den Baum relevanten Wahrscheinlichkeiten.
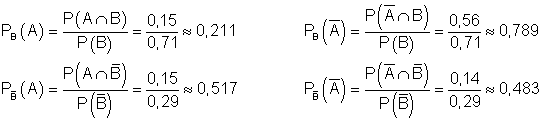
c)
Von allen Zuschauern, von den man weiß, das sie eine positive Meinung über die Sendung hatten, waren 78,9% älter als 25 Jahre.
![]()
d)
Von allen Zuschauern, von den man weiß, das sie älter als 25 sind, hatten 20% eine negative Meinung über die Sendung.
![]()
e)
Das Ereignis B ist abhängig vom Ereignis A. Das bedeutet, die positive Meinung über die Fernsehsendung ist vom Alter der Zuschauer abhängig.
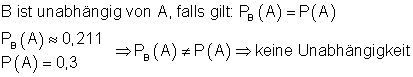
2.
In einem Land der Dritten Welt leiden 1% der Menschen an einer bestimmten Infektionskrankheit. Ein Test zeigt die Krankheit bei den tatsächlich erkrankten zu 98% korrekt an. Leider zeigt der Test auch 3% der Gesunden als erkrankt an.
a) Stelle den Sachzusammenhang in einer 4- Feldtafel da. Verwenden Sie die Ereignisse (mit ihren Gegenereignissen):
K: Die getestete Person ist krank.
T: Testergebnis ist positiv (Person wurde als krank getestet).
b) Zeichne das Baumdiagramm und den inversen Baum.
Bestimmen Sie alle Pfadwahrscheinlichkeiten.
c) Mit welcher Wahrscheinlichkeit zeigt der Test bei einer zufällig ausgewählten Person ein positives Ergebnis?
d) Mit welcher Wahrscheinlichkeit ist eine als positiv getestete Person auch tatsächlich krank? Kommentiere das Ergebnis.
e) Mit welcher Wahrscheinlichkeit ist eine als negativ getestete Person gesund? Kommentiere das Ergebnis.
2. Ausführliche Lösungen
a)

b) Baumdiagramm:
Berechnung aller für den Baum relevanten Wahrscheinlichkeiten.
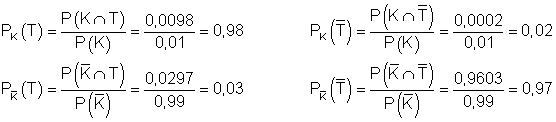
Der inverse Baum:
Berechnung aller für den Baum relevanten Wahrscheinlichkeiten.

c)
Bei einer zufällig ausgewählten Person zeigt der Test mit einer Wahrscheinlichkeit von 0,0395 ein positives Ergebnis an.
![]()
d)
Eine Person, von der man weiß, dass sie positiv getestet wurde, ist mit einer Wahrscheinlichkeit von 0,2481 auch tatsächlich krank.
Kommentar: Das Ergebnis von ca. 25% ist nicht zufriedenstellend. Nur 25% aller positiv getesteten sind tatsächlich erkrankt. Das bedeutet, dass ca. 75% der positiv getesteten gesund sind. Es wäre wünschenswert, dass der Test verbessert wird.
![]()
e)
Eine Person, von der man weiß, dass sie negativ getestet wurde, ist mit einer Wahrscheinlichkeit von 0,999792 auch tatsächlich gesund.
Kommentar: In diesem Fall ist das Ergebnis von ca. 99,98% sehr zufriedenstellend. Nur ca. 0,02% der als negativ getesteten Personen sind tatsächlich krank.
![]()
3.
An einem Berufskolleg werden alle 674 Schüler/innen befragt ob sie rauchen oder nicht rauchen. Das Ergebnis der Befragung sieht wie folgt aus:
82 der insgesamt 293 Schüler (männlich) gaben an zu rauchen.
250 Schülerinnen gaben an, nicht zu rauchen.
a) Stelle den Sachzusammenhang in einer 4-Feldertafel dar. Verwenden Sie die Ereignisse (mit ihren Gegenereignissen):
A: Die Person ist männlich.
B: Die Person ist Raucher
b) Mit welcher Wahrscheinlichkeit ist eine zufällig ausgewählte Person weiblich und Nichtraucherin?
c) Der Schulleiter sieht eine Schülerin im Aufenthaltsraum. Mit welcher Wahrscheinlichkeit ist diese Schülerin Nichtraucherin?
d) Untersuche, ob das Ereignis „männlich“ und das Ereignis „Raucher“ voneinander abhängige Ereignisse sind.
3. Ausführliche Lösungen
a)

b)
Eine zufällig ausgewählte Person ist mit einer Wahrscheinlichkeit von 0,371 weiblich und raucht nicht.
![]()
c)
Eine Person, von der man weiß, das sie weiblich ist, ist mit einer Wahrscheinlichkeit von 0,656 Nichtraucherin.
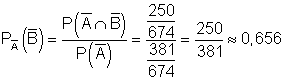
d)
Die Ereignisse A: „Mann“ und B: „Raucher“ sind voneinander abhängig.
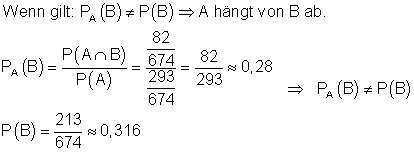
Hier findest du die Aufgaben hierzu.
Und hier die Theorie hierzu.
Hier findest du eine Übersicht über alle Beiträge zum Thema Wahrscheinlichkeitsrechnung, darin auch Links zu Aufgaben.