Hier findest du die Lösungen zu den Aufgaben zur bedingten Wahrscheinlichkeit.
1.
In einem Großversuch wurde ein Medikament getestet. Die Ergebnisse sind in einer Tabelle festgehalten. Dabei bedeuten:

a) Stelle die relativen Häufigkeiten in einer Vierfeldertafel dar und zeichne das dazugehörige Baumdiagramm.
b) Wie groß ist die Wahrscheinlichkeit bei einer Person, von der man weiß, dass sie das Medikament eingenommen hat, zu gesunden?
c) Wie groß ist die Wahrscheinlichkeit bei einer Person, von der man weiß, dass sie das Placebo eingenommen hat, nicht zu gesunden?
1. Ausführliche Lösungen
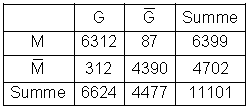
a) Die Vierfeldertafel:

Das Baumdiagramm:
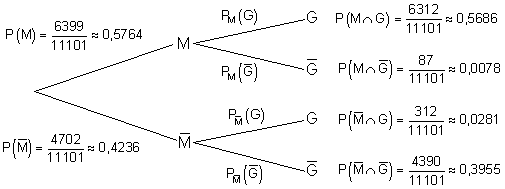
b)
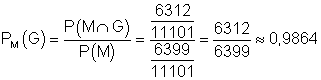
Bei einer Person, von der man weiß, dass sie das Medikament eingenommen hat, ist die Wahrscheinlichkeit 0,9864, dass sie gesund geworden ist.
c)
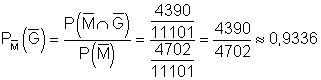
Bei einer Person, von der man weiß, dass sie ein Placebo eingenommen hat, ist die Wahrscheinlichkeit 0,9336, dass sie nicht gesund geworden ist.
2.
In einer Gruppe von 900 Personen haben sich 600 prophylaktisch gegen Grippe impfen lassen. Nach einer bestimmten Zeit wurde jedes Gruppenmitglied danach befragt, wer an einer Grippe erkrankte. Die Ergebnisse werden in einer 4-Feldertafel dargestellt.

Das Ereignis A sei „Person ist geimpft“ und das Ereignis B: „Person erkrankt“.
Berechnen Sie:
![]()
Gib die Bedeutung der einzelnen Ergebnisse in Textform an.
2. Ausführliche Lösung
![]()
![]()
I. Bei der zufälligen Auswahl einer Person ist die Wahrscheinlichkeit dafür, eine geimpfte Person zu finden 0,666…
![]()
II. Bei der zufälligen Auswahl einer Person ist die Wahrscheinlichkeit dafür, eine erkrankte Person zu finden 0,2.
![]()
III. Bei der zufälligen Auswahl einer Person ist die Wahrscheinlichkeit dafür, eine trotz Impfung erkrankte Person zu finden 0,06666…
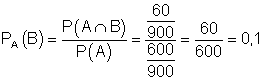
IV. Eine Person, von der man weiß, dass sie geimpft wurde ist mit einer Wahrscheinlichkeit von 0,1 dennoch erkrankt.
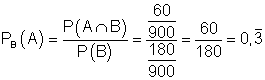
V. Eine Person, von der man weiß, dass sie erkrankt ist, wurde ist mit einer Wahrscheinlichkeit von 0,333… geimpft.
![]()
VI. Bei der zufälligen Auswahl einer Person, ist die Wahrscheinlichkeit eine nicht geimpfte und auch erkrankte Person zu finden 0,1333…
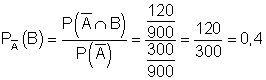
VII. Eine Person, von der man weiß, dass sie nicht geimpft wurde ist mit einer Wahrscheinlichkeit von 0,4 auch erkrankt.
3.
Mehr Abiturientinnen als Abiturienten:
52,4% der 244600 Jugendlichen, die am Ende des vergangenen Schuljahres ihre Schule mit der allgemeinen Hochschulreife verließen, waren Frauen. In den neuen Ländern und Berlin liegt der Frauenanteil mit 59,1% deutlich höher als im früheren Bundesgebiet (50,8%).
a) Stell eine 4-Feldertafel auf, die diesen Sachzusammenhang beschreibt.
b) Zeichne ein Baumdiagramm mit dem 1. Merkmal „Herkunft“ (Ost, West) und dem 2. Merkmal „Geschlecht“ (männlich, weiblich).
c) Zeichne ein Baumdiagramm mit dem 1. Merkmal „Geschlecht“ (männlich, weiblich) und dem 2. Merkmal „Herkunft“ (Ost, West).
d) Aus der Gesamtheit aller Abiturientinnen und Abiturienten des betrachteten Jahrgangs wurde eine Person zufällig ausgewählt.
(1) Mit welcher Wahrscheinlichkeit stammt diese Person aus Ostdeutschland?
(2) Mit welcher Wahrscheinlichkeit ist die ausgewählte Person eine Frau?
(3) Falls diese Person aus Ostdeutschland kommt, mit welcher Wahrscheinlichkeit ist dies ein Mann?
(4) Falls diese Person eine Frau ist, mit welcher Wahrscheinlichkeit stammt sie aus Westdeutschland?
3. Ausführliche Lösungen
a)

b)
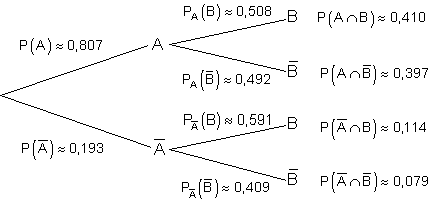
Berechnung aller für den Baum relevanten Wahrscheinlichkeiten.
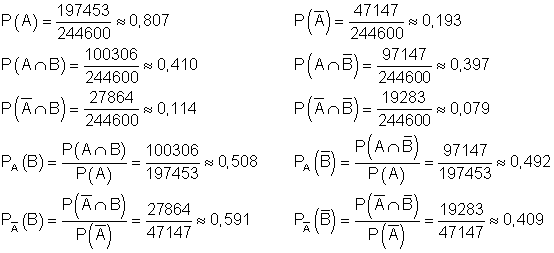
c)
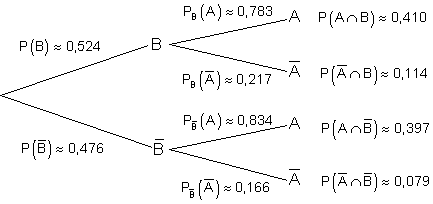
Berechnung aller für den Baum relevanten Wahrscheinlichkeiten.
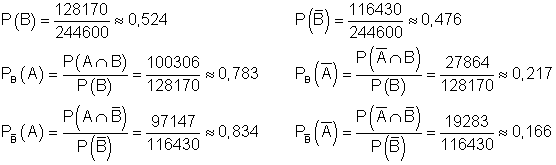
d) (1)
![]()
Die zufällig ausgewählte Person stammt mit einer Wahrscheinlichkeit von 19,3% aus den neuen Bundesländern (Ost).
(2)
![]()
Die zufällig ausgewählte Person ist mit einer Wahrscheinlichkeit von 52,4% weiblich.
(3)
![]()
Wenn man weiß, dass die zufällig ausgewählte Person aus den neuen Bundesländern stammt, dann ist diese mit einer Wahrscheinlichkeit von40,9% männlich.
(4)
![]()
Wenn man weiß, dass die zufällig ausgewählte Person weiblich ist, dann stammt sie mit einer Wahrscheinlichkeit von 78,3% aus den alten Bundesländern (West).
Hier findest du die Aufgaben hierzu.
Und hier die Theorie hierzu.
Hier findest du eine Übersicht über alle Beiträge zum Thema Wahrscheinlichkeitsrechnung, darin auch Links zu Aufgaben.

