In diesem Beitrag erkläre ich alles Wichtige zum Satz des Pythagoras. Zuerst definiere ich die Bezeichnungen im rechtwinkligem Dreieck, Hypotenuse und Kathete. Danach stelle ich die Formel des Satz des Pythagoras vor und beweise sie anhand einer Zeichnung. Anschließend führe ich die Rechnung anhand einiger Beispielaufgaben vor.
Definition Hypotenuse:
Im rechtwinkligen Dreieck nennt man die Seite, die dem rechten Winkel gegenüberliegt, Hypotenuse.
Definition Kathete:
Die den rechten Winkel einschließenden Seiten heißen Katheten.
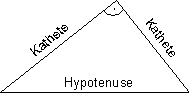
Satz des Pythagoras Beweis und Formel
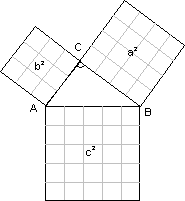
Wenn wir aus allen drei Seiten des Dreiecks Quadrate machen, dann ist die Fläche aus den beiden Katheten genauso groß wie die Fläche aus der Hypotenuse. Dies können Sie leicht in der Zeichnung erkennen. Mathematisch ausgedrückt heißt das:
Im rechtwinkligen Dreieck hat das Hypotenusenquadrat denselben Flächeninhalt wie die beiden Kathetenquadrate zusammen.
Hierzu die Formel:
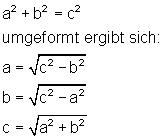
Das kann sehr hilfreich sein, wenn wir nur einen Teil der Informationen eines rechtwinkligen Dreiecks haben. Hierzu ein paar
Beispielaufgaben zum Satz des Pythagoras:
Berechnen Sie die fehlenden Längen in einem rechtwinkligem Dreieck!
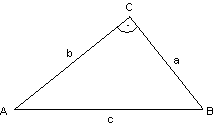
a)![]()
b)![]()
c)![]()
Lösung:a)
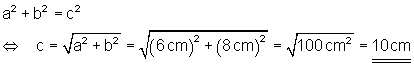
b)
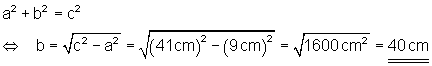
c)
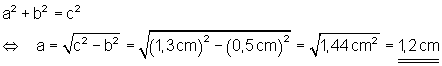
Hier findest duAufgaben zum Satz des Pythagoras aus der Technik I.
Hier eine Tabellen zum Umrechnen von Zehnerpotenzen, Längen, Flächen, Volumen mit Übungsaufgaben und Lösungen.
Und hier eine Übersicht über alle Beiträge zum Thema Geometrie, darin auch Links zu weiteren Aufgaben.


