Hier findest du die Aufgaben und Lösungen zu Pythagoras aus der Technik I.
Lösungen mit dem Casio fx-CG20 und Casio fx-CG50 weiter unten
1. Gartentor
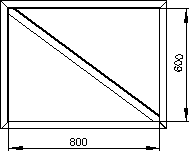
Ein Laie will ein Gartentor aus Vierkantprofil (40×40) fertigen. Es soll so aussehen wie die Zeichnung unten.
Bestimme die Gesamtlänge der benötigten Profilstäbe, wenn Sie mit einem Verschnitt von 5 % rechnen!
Der Laie sägt die Stäbe erst gerade ab. Du brauchst dabei also nicht zurücksichtigen, dass er sofort 45 ° Winkel sägt!
2. Berechne die fehlenden Längen!
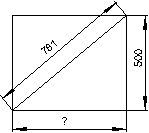
a)
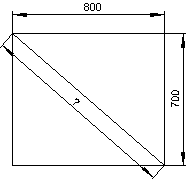
b)
3. Doppeltor
Jetzt soll der Schreiner ein Doppeltor aus Vierkantprofil (50 x 50) fertigen.
Welche Gesamtlänge an Stäben ist nötig, wenn der Verschnitt 4% beträgt?
Beachte, wie die Profile zusammengebaut werden! Das heißt, berücksichtige bei der Berechnung der Querstäbe, dass diese innen liegen. Das innere Rechteck ist also auf jeder Seite 50 mm kleiner!

4. Straßenlaterne
In der Mitte zwischen zwei Häusern wird an einem Spannseil eine Straßenlaterne aufgehängt. Das Spannseil hat genau eine Länge von l = 6,4 m. Nachdem die Lampe angebracht wurde, hängt das Seil etwas durch.
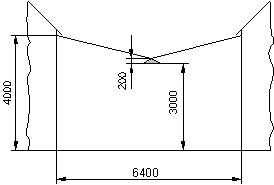
a) Um welche Länge wurde das Seil durch die Belastung gedehnt?
b) Wie viel % wird das Seil gedehnt?
Lösungen
1. Gartentor
Ausführliche Lösung:
Bei der Berechnung der Längen müssen wir den Querschnitt des Vierkantprofils berücksichtigen. Das Rechteck besteht aus zwei waagerechten Streben der Länge 880 mm und aus zwei senkrechten Streben der Länge 680 mm. Die Länge der Querstrebe kann man dabei mit dem Pythagoras berechnen.
5% Verschnitt bezieht sich auf die insgesamt benötigte Länge. Das sind 100%, mit anderen Worten Grundwert. Die verminderte Länge kommt zustande, indem man von der insgesamt benötigten Länge 5% Verschnitt abzieht. 95% bedeutet, die insgesamt ermittelte Länge ist nur 0,95 mal so groß wie die benötigte Länge.

Insgesamt benötigt der Schreiner 4337 mm bzw. 4,337 m Profilstäbe .
2. Berechne die fehlenden Längen!
a)
Ausführliche Lösung:
Die gesuchte Länge entspricht der Kathete des rechtwinkligen Dreiecks. Diese können wir mit dem Satz des Pythagoras berechnen.
![]()
Die Länge der gesuchten Kathete beträgt etwa 0,6 m.
2. b)
Ausführliche Lösung:
Die zu bestimmende Länge entspricht der Hypotenuse des rechtwinkligen Dreiecks. Diese lässt sich ebenfalls mit dem Satz des Pythagoras berechnen.
![]()
Die gesuchte Länge entspricht der Hypotenuse, also beträgt sie etwa 1,063 m.
3. Doppeltor
Ausführliche Lösung:
Bei der Berechnung der jeweiligen Längen müssen wir ebenfalls den Querschnitt des Vierkantprofils berücksichtigen. Das Tor besteht aus zwei Rechtecken mit jeweils einer Querstrebe. Das Rechteck besteht aus zwei waagerechten Streben der Länge x und aus zwei senkrechten Streben der Länge y. Die Länge der Querstrebe können wir ebenfalls mit dem Pythagoras berechnen.
4% Verschnitt bezieht sich auf die insgesamt benötigte Länge. Alle Maße sind in der Einheit mm angegeben. Wenn man das berücksichtigt, kann bei der Rechnung die Einheit weggelassen, sofern die Zahlenangaben mm entsprechen. Das Endergebnis versehen wir dann wieder mit der Einheit mm bzw. m.


Insgesamt benötigt der Schreiner 23134 mm bzw. 23,134 m Profilstäbe.
Zwischenrechnungen wurden auf drei Stellen gerundet. Das Endergebnis auf ganze Millimeter.
Lösung mit dem Casio fx-CG20
Eine Einführung in den Casio fx-CG20 und Casio fx-CG50 finden Sie hier.
Dort finden Sie auch eine Anleitung, wie man den Casio fx-CG20 auf den Casio fx-CG50 updaten kann.
Bemerkung zum Variablenspeicher
Lösungen mit dem GTR Casio fx-CG 20 unter Verwendung der Variablenspeicher
Wenn Zwischenergebnisse gerundet werden, ist das Endergebnis fehlerbehaftet. Die Größe des Fehlers hängt davon ab, wie stark gerundet wird und in wieviel Stufen der Rechnung gerundet wird. In den Beispielen hier habe ich Zwischenergebnisse in Variablenspeicher geschoben und mit denen weitergrechnet.
Rechnung mit gerundeten Zwischenergebnissen.
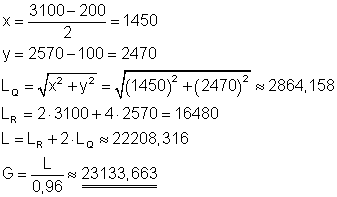
Rechnung mit Variablenspeicher.
Die folgende Darstellung zeigt, was im Rechnerdisplay erscheint. Dabei setze ich die elementaren Eingabetechniken voraus. Exakte Eingabebeispiele finden Sie weiter unten.
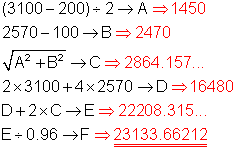
Das exakte Ergebnis unterscheidet sich erst in der 3. Stelle nach dem Komma vom Ergebnis, in dem die Zwischenwerte auf drei Stellen hinter dem Komma gerundet wurden.
Exakte Eingabeprozedur. Jede Zeile wird in einen Variablenspeicher geschoben.

4. Straßenlaterne
a)
Die Länge des gedehnten Seiles ist aus Symmetriegründen die doppelte Länge der Hypotenuse des in nebenstehender Skizze eingezeichneten Dreiecks.
Aus den angegebenen Maßen sind die Katheten x und y zu berechnen.
Mit dem Satz des Pythagoras erhält man die Länge der Hypotenuse.
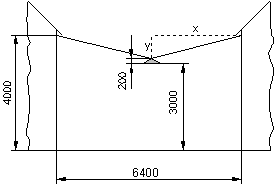
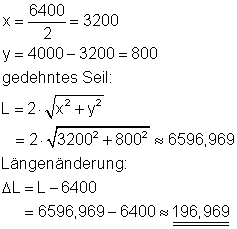
Die Längenänderung des Seils beträgt etwa 197 mm bzw. 0,197 m.
4. b)
Gesucht ist der Prozentsatz der Längenänderung bezogen auf die Länge des ungedehnten Seiles.
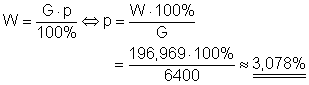
Die Längenänderung beträgt etwa 3,078%.
Lösung mit dem Casio fx-CG20
Hier finden Sie eine Einführung in den graphikfähigen Taschenrechner.
Rechnung mit gerundeten Zwischenergebnissen.
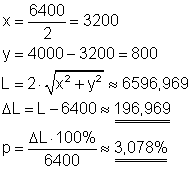
Rechnung mit Variablenspeicher.
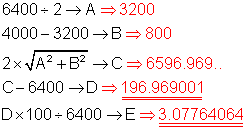
Das exakte Ergebnis unterscheidet sich erst in der 3. Stelle nach dem Komma vom Ergebnis, in dem die Zwischenwerte auf drei Stellen hinter dem Komma gerundet wurden.
Exakte Eingabeprozedur. Jede Zeile wird in einen Variablenspeicher geschoben.

Dazu findest du hier die Theorie.
Und hier weitere Aufgaben und Lösungen zu Pythagoras aus der Technik II.
Weitere Beispiele zu dem Casio fx-CG20 finden Sie in der Kategorie GTR
und in der Übersicht über alle Beiträge zum grafikfähigen Taschenrechner Casio fx-CG20.
Außerdem hier eine Tabellen zum Umrechnen von Zehnerpotenzen, Längen, Flächen, Volumen mit Übungsaufgaben und Lösungen.
Und hier eine Übersicht über alle Beiträge zum Thema Geometrie, darin auch Links zu weiteren Aufgaben.

