Aufgaben, Lösungen Pythagoras Technik II

Hier findest du Aufgaben und Lösungen zum Satz des Pythagoras aus der Technik II.

1. Vier Seile sollen einen Mast in seiner Position halten.

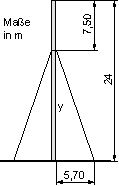
Die Seile werden x = 5,70 m vom Mast entfernt am Boden befestigt.

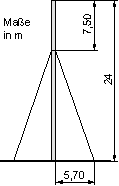
a) Wie lang muss jedes Seil mindestens sein?
b) Um wie viel % vergrößert sich die Länge eines Seils, wenn der seitliche Befestigungspunkt am Boden um p = 10% weiter nach außen gelegt wird?

2. Ein Schreiner will ein Gewächshaus

aus aus Vierkantstäben (60 x 40) zu bauen. Dafür erstellt er diese Bauzeichnung:

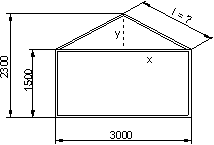
a) Auf welche Länge muss er die Streben sägen?
b) Das gesamte Gewächshaus besteht aus 6 Elementen, die durch 1 m lange Verbindungselemente an den 5 Fügstellen zusammen geschraubt werden. Wie viel m Vierkantstäbe braucht der Schreiner insgesamt?

3. Ein Ausleger soll vom Drehgestell aus eine Förderhöhe von 3 m haben.

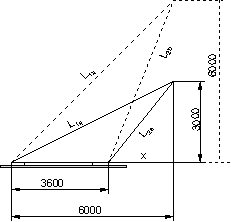
a) Wie lang müssen die Streben L_1a und L_2a sein?
b) Wie lang wären die Streben L_1b und L_2b, wenn die Förderhöhe doppelt so hoch ist, also 6 m?
c) Um wie viel % sind im Fall b) die Streben länger?

4. Eine Druckstrebe mit d₁ = 3,2 m stützt einen Ausleger.

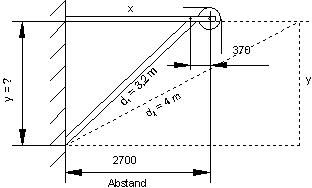
a) Wie groß ist der Abstand y der beiden Lager?
b) Auf welches Maß ändert sich der Abstand 2700, wenn die Druckstrebe auf d₂ = 4 m verlängert wird, der Lagerabstand y aber gleich bleibt?

---

 

Lösungen

1. Vier Seile sollen einen Mast in seiner Position halten.

a)

Ausführliche Lösung:

Das Seil bildet die Hypotenuse eines rechtwinkligen Dreiecks. Die waagerechte Kathete ist 5,7 m lang, die senkrechte Kathete y können wir mit dem Satz des Pythagoras berechnet. Dann kennen wir die Seillänge.
Da alle Maße in der Einheit m gegeben sind, können wir bei der Berechnung die Einheit fortlassen. Das Ergebnis versehen wir dann wieder mit der Einheit. Ich habe mit einer Rechengenauigkeit von drei Stellen hinter dem Komma gerechnet.

 

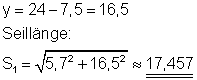
Jedes Seil muss mindestens 17,457 m lang sein.

1. b)

Ausführliche Lösung:

Nachdem der seitliche Befestigungspunkt 10% länger ist, können wir die neue Seillänge wie unter Aufgabenteil a) berechnen. Die prozentuale Seilverlängerung bezieht sich auf die unter a) berechnete Länge.

Die Seillänge vergrößert sich um etwa 1,111%. Das Ergebnis enthält geringe Rundungsfehler, da die Zwischenwerte auf drei Stellen hinter dem Komma gerundet sind. Um das exakte Ergebnis zu erhalten, müsste man die Zwischenergebnisse im Taschenrechner speichern und damit weiterrechnen. Im Fall der aktuellen Aufgabe wäre die prozentuale Seilverlängerung dann 1,113% anstatt 1,111%.

Die Taschenrechnereingabe (TI-30 eco RS) wäre:

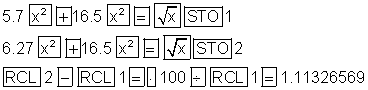
2. Ein Schreiner will ein Gewächshaus

aus aus Vierkantstäben (60 x 40) zu bauen. Dafür erstellt er diese Bauzeichnung:

a)

Ausführliche Lösung:

Die Strebe tritt als Hypotenuse eines rechtwinkligen Dreiecks auf. Aus den Maßangaben der Zeichnung können wir mit dem Satz des Pythagoras die Katheten x und y berechnen. Ich habe mit einer Recheneinheit von mm auf drei Stellen gerechnet. Das Endergebnis in m.

 

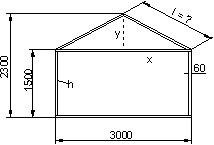
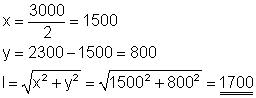
Die Streben müssen auf eine Länge von 1700 mm bzw. 1,7 m gesägt werden.

2. b)

Ausführliche Lösung:

Um die Höhe h zu berechnen, müssen wir das Profilmaß (60 x 40) berücksichtigen. Dabei werden die waagerechten Elemente aus Stabilitätsgründen hochkant eingesetzt. Es gibt 6 gleiche Giebelelemente, die 5 mal durch 1 m lange Verbindungselemente an jeweils 5 Stellen zusammengeschraubt werden.

Insgesamt braucht man 97960 mm bzw. 97,96 m Vierkantstäbe.

3. Ein Ausleger soll vom Drehgestell aus eine Förderhöhe von 3 m haben.

a)

Ausführliche Lösung:

Beide Streben bilden die Hypotenuse eines rechtwinkligen Dreiecks. Die Längen der Katheten können wir aus der Maßvorgabe berechnen.

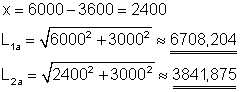
Die Strebe L_1a ist etwa 6708,204 mm bzw. 6,708 m lang.
Die Strebe L_2a ist etwa 3841,875 mm bzw. 3,842 m lang.

3. b)

Ausführliche Lösung:

Beide Streben bilden genau wie bei Aufgabe 3a die Hypotenuse eines rechtwinkligen Dreiecks. Die senkrechte Kathete ist jetzt 6000 mm lang, die waagerechten bleiben unverändert.

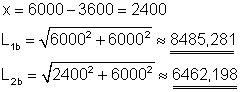
Die Strebe L_1b ist etwa 8485,281 mm bzw. 8,485 m lang.
Die Strebe L_2b ist etwa 6462,198 mm bzw. 6,462 m lang.

3. c)

Ausführliche Lösung:

Die prozentuale Verlängerung bezieht sich auf die Längen aus Aufgabenteil a)

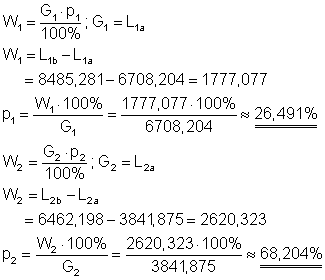
Die Strebe L_1b =26,491% länger als die Strebe L_1a.
Die Strebe L_2b =68,204% länger als die Strebe L_2a.

4. Eine Druckstrebe mit d₁ = 3,2 m stützt einen Ausleger.

a)

Ausführliche Lösung:

Das Maß y ist eine Kathete des rechtwinkligen Dreiecks mit vorgegebener Hypotenuse . Die Kathete x können wir aus der Bemaßung berechnen.

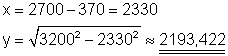
Der Lagerabstand y beträgt 2193,422 mm bzw. 2,193 m.

4.b)

Ausführliche Lösung:

Bei vorgegebener Hypotenusenlänge und der senkrechten Kathete y aus Aufgabenteil a) können wir die waagerechte Kathete berechnen.

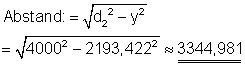
Der Abstand 2,7 m ändert sich auf 3,345 m.

Hier findest du die Theorie dazu.

Und hier weitere Aufgaben zum Satz des Pythagoras aus der Technik I

Hier eine Tabellen zum Umrechnen von Zehnerpotenzen, Längen, Flächen, Volumen mit Übungsaufgaben und Lösungen.

Und hier eine Übersicht über alle Beiträge zum Thema Geometrie, darin auch Links zu weiteren Aufgaben.