Bevor ich die Aufgaben zum Thema Terme zusammenfassen vorstelle, gebe ich ein paar Tipps, wie man Terme zusammenfasst.
Dazu können dir diese Videos helfen:
Tipps zum Terme zusammenfassen
Bei der Vereinfachung von Termen geht man wie Folgt vor:
Terme ohne Brüche und Klammern zusammenfassen:
Wir ordnen die Summanden alphabetisch nach den Variablen und fassen sie zusammen.
1. Summanden ordnen 3x + 4y – 2z + 4y – 2x
2. zusammenfassen = 3x – 2x + 4y + 4y – 2z
Ergebnis: = x + 8y – 2z
Terme ohne Brüche mit einfachen Klammern zusammenfassen:
Zuerst lösen wir die Klammern auf. Beachte dabei, dass du die Plusklammern weglassen kannst.
Wenn du jedoch eine Minusklammer auflöst, ändern sich die Vorzeichen aller Summanden. Danach kannst du die Summanden alphabetisch nach den Variablen ordnen und zusammenfassen.
1. Klammern auflösen 12x – (12x + 3y) + 4y – (3x + 2y)
2. Summanden ordnen = 12x – 12x – 3y + 4y – 3x – 2y
3. zusammenfassen = 12x – 12x – 3x – 3y + 4y – 2y
Ergebnis: = -3x – y
Terme ohne Brüche mit verschachtelten Klammern:
Zuerst sollte man die Klammern nach den Klammerregeln von Innen nach außen aufgelöst. Zuerst die inneren Klammern, dann die äußeren Klammern und immer schön der Reihe nach. Danach fasst man die Summanden alphabetisch nach den Variablen geordnet und zusammen.
1. innere Klammer auflösen 4x – [8y – (3x + 2z) – (x + 2y – 4z)]
2. äußere Klammer auflösen = 4x – [8y – 3x + 2z – x – 2y + 4z]
3. Summanden ordnen = 4x – 8y + 3x + 2z + x + 2y – 4z
4. zusammenfassen = 4x + 3x + x – 8y + 2y + 2z -4z
Ergebnis: = 8x – 6y – 2z
Terme mit Brüchen zusammenfassen:
Man ordnet die Summanden alphabetisch nach den Variablen. Gleiche Variablen kann man jedoch nur dann zusammenfassen, wenn die zugehörigen Brüche gleichnamig sind.
Terme mit Brüchen in der gemischten Schreibweise (gemischte Brüche):
Man verwandelt die gemischten Brüche in unechte Brüche. Dann ordnet man die Summanden alphabetisch nach den Variablen. Gleiche Variablen kann man nur dann zusammenfassen, wenn die zugehörigen Brüche gleichnamig sind.
Beachte: Klammern löst man von innen nach außen. Zuerst also die runden Klammern, dann die eckigen Klammern. Eine Plusklammer kann man einfach weglassen. Löst man eine Minusklammer auf, so ändern sich die Vorzeichen aller Summanden in der Klammer
Aufgaben
1. Löse die Klammern auf und fasse zusammen.
a) 4c – 10c + (-4c) + 5c
b) – (-4a) + 6a – 3a + (-2a)
Diese Aufgabe erkläre ich in diesem
shorts Terme zusammenfassen.
2. Ordne die Summanden und fasse zusammen.
a) 6x + 8y – 2x + 14y
b) 12k + 4m – 5n + 6k – 2n – 3m
3. Ordne die Summanden und fasse zusammen.
a)
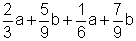b)
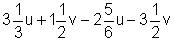4. Löse die Klammern auf und fasse zusammen.
a) 16a – 2x + 4a – 2(x – a) – 4(a + 3x)
b) 16ax – 3ax + 5a (-3x)
5. Löse die Klammern auf und fasse zusammen.
a) 12x – (12x + 3y) + 4y – (3x +2y)
b) 8m – 6n – (3n – m) – (2m + n) + 4m
6. Löse die Klammern auf und fasse zusammen.
a) 2u + [ 5 – (3u – 1) + 7u] + 8
b) 4x – [8y – (3x + 2z) – (x + 2y – 4z)]
7. Löse die Klammern auf und fasse zusammen.
a) 25s – [4s – (12s + 8t) + (25t + 12s)]
b)
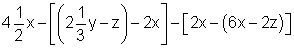8. Löse die Klammern auf und fasse zusammen.
a) (2u + v – 4w) – [2v – (4u + v – 2w)]
b) (x – 10) – [2x – (10x – 14)] – [2 + (4 – 2x)]
9. Löse die Klammern auf und fasse zusammen.
a) 8m – 6n – [6m – (4n – 2m) – (4m + 2n)]
b)
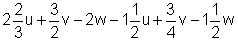10. Verwandle die Brüche und fasse zusammen.
a) 1,6x + 2,5y – 3,1z – 1,2x – 2,4y + 2z
b)
Hier findest du die Lösungen.
Und hier eine Übersicht über alle Beiträge zum Thema Terme und zu anderen mathematischen Grundlagen, darin auch Links zu weiteren Aufgaben.
