In diesem Beitrag zeige ich, wie man mit dem grafikfähigen Taschenrechner Casio fx-CG50 und Casio fx-CG20 ein lineares Gleichungssystem mit drei Variablen löst. Dabei unterscheide ich zwischen Gleichungssystemen mit eindeutiger, keiner und unendlich vielen Lösungen.
Eine Einführung in den Casio fx-CG20 und Casio fx-CG50 findest du hier.
Casio fx-CG20 auf Casio fx-CG50 updaten
Wer noch den Casio fx-CG20 hat, kann sich auf der Webseite der Firma ein kostenloses Update herunterladen. Dann kannst du auch die neuen Funktionen des Casio fx-CG50 nutzen. Suche dazu auf Casio-Webseite nach ‚FX-CG20 & FX-CG50 Betriebssystem-Update‘. Ich gebe hier nicht den direkten Link ein, weil es in der Zwischenzeit vielleicht bereits ein neueres Update gibt.
Es gibt mehrere Verfahren, ein lineares Gleichungssystem mit dem GTR zu lösen.
An dieser Stelle erläutere ich das Matrixverfahren. Bei Gleichungssystemen gibt es grundsätzlich drei Arten von Lösungen,
Das Gleichungssystem
- ist eindeutig lösbar.
- hat keine Lösung.
- hat unendlich viele Lösungen.
Lineares Gleichungssystem mit drei Variablen und eindeutiger Lösung
Zuerst wandelt man das Gleichungssystem in die entsprechende Matrix um.
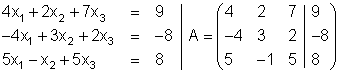
Befehlssequenz der Eingabe:
Siehe auch Matrixeingabe und Diagonalisierung.
Run-Matrix öffnen: [MENU] 1.
Den-Matrixeditor öffnen: {MAT/VCT}.
Dimension der Matrix bestimmen: [EXE] 3 [EXE] 4 [EXE].
Das Eingabefenster öffnen: [EXE].
Die Eingabesequenz obiger Matrix lautet:
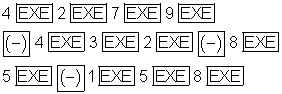 .
.
Abschluss der Eingabe mit [EXIT] [EXIT].
Um dann die Lösungsmenge des Gleichungssystems zu erhalten, diagonalisieren man die Matrix:
Diagonalisieren der Matrix A:
[OPTN] {MAT/VCT}
[F6] {Rref}
[F6] [F6] [F6] {MAT}
A[A] [EXE].
Aus der Diagonalmatrix kann man die Lösungsmenge des Gleichungssystems in der 4. Spalte ablesen.
Dieses Gleichungssystem ist also eindeutig lösbar.
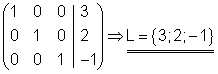 .
.
Lineares Gleichungssystem mit drei Variablen und keiner Lösung
Das Gleichungssystem lautet:
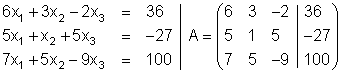 .
.
Für die Eingabe gehen wir davon aus, dass man sich bereits im Menü Run-Matrix befindet.
Den-Matrixeditor öffnen: {MAT/VCT}.
Dimension der Matrix bestimmen: [EXE] 3 [EXE] 4 [EXE].
Das Eingabefenster öffnen: [EXE].
Die Eingabesequenz obiger Matrix lautet:
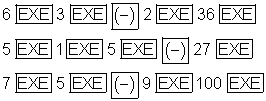
Abschluss der Eingabe mit [EXIT] [EXIT].
Diagonalisieren der Matrix A:
[OPTN] {MAT/VCT}
[F6] {Rref}
[F6] [F6] [F6] {MAT}
A[A] [EXE]
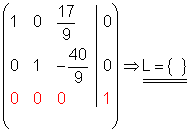 .
.
Die letzte Zeile der Matrix gehört zur Gleichung
![]()
Dies ist ein Widerspruch, der aus der Annahme der Lösbarkeit entstanden ist.
Das Gleichungssystem ist folglich nicht lösbar.
Merke
Falls die Matrixumformung dazu führt, dass eine Zeile entsteht, in der sich links nur Nullen befinden und rechts eine von Null verschiedene Zahl u, dann lautet die Gleichung 0 = u.
Dies ist ein Widerspruch gegen die Annahme der Lösbarkeit des Gleichungssystems.
Es gibt also keine Lösung. Die Lösungsmenge ist folglich leer.
Lineares Gleichungssystem mit drei Variablen und unendlich vielen Lösungen
Das Gleichungssystem lautet:
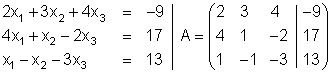
Den-Matrixeditor öffnen: {MAT/VCT}.
Dimension der Matrix bestimmen: [EXE] 3 [EXE] 4 [EXE].
Das Eingabefenster öffnen: [EXE].
Die Eingabesequenz obiger Matrix lautet:
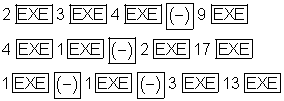
Abschluss der Eingabe mit [EXIT] [EXIT].
Diagonalisieren der Matrix A:
[OPTN] {MAT/VCT}
[F6] {Rref}
[F6] [F6] [F6] {MAT}
A[A] [EXE]
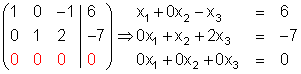 .
.
Da die 3. Zeile nur Nullen enthält, ist eine Gleichung überflüssig, man wählt x3 = t.
Danach werden die 1. und 2. Zeile nach x1 und x2 aufgelöst.
![]()
Merke: Ergibt eine Matrixumformung eine Zeile mit lauter Nullen, dann ist die zugehörige Gleichung entbehrlich.
Daher kann man eine Variable frei wählen.
Die Lösungsmenge hat dann unendlich viele Lösungen.
Dazu findest du weitere Beispiele in der Kategorie GTR.
Außerdem in der Übersicht über alle Beiträge zum grafikfähigen Taschenrechner Casio fx-CG20.


