Im letzten Beitrag hatte ich anhand eines praktischen Beispiels in die Integralrechnung eingeführt. Hier erkläre ich jetzt Schritt für Schritt die Flächeninhaltsfunktion und Stammfunktion. Zuerst zeige ich anhand einer Funktion ersten Grades, dass die Funktion F(x0) die Fläche zwischen dem Graphen und der x-Achse beschreibt. Danach erkläre ich, wie man eine krummlinig begrenzte Fläche in endlich viele Flächen zerlegen kann. Mit anderen Worten: das Flächenproblem, Flächeneinschachtelung. Danach definiere ich die Begriffe ableiten und Stammfunktion. Anhand eines Beispiels zeige ich, wie man die Stammfunktion sucht und stelle die Regel dazu vor. Es gibt jedoch nicht nur eine, sondern die Menge der Stammfunktionen. Zuletzt stelle ich Trainingsaufgaben zum Berechnen von Stammfunktionen zur Verfügung.
Beispiel: Fläche bei einer Funktion 1. Grades


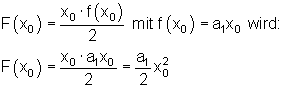
![]()
Mit anderen Worten: Flächenfunktion oder Flächeninhaltsfunktion.
Beispiel:
f(x) = 2x mit x_0 = 3 \Rightarrow f(x_0) = 6
Mit der Flächenberechnung für Dreiecke ergibt sich daraus:
A=\dfrac{g \cdot h}{2} \Rightarrow A = \dfrac{3 \cdot 6}{2} = 9
Mit der Formel, die wir oben hergeleitet haben dann:
F(3)=\dfrac{a_1}{2}x_0^2 = \dfrac{2}{2}3^2 = 9
Die Flächenfunktion ist deshalb
F(x)=\dfrac{2}{2} x^2
Wenn wir die Flächenfunktion ableiten, ergibt sich unsere ursprüngliche Funktion: F'(x)=2x = f(x).
Dazu könnt ihr euch das 📽️Video Flächenberechnung mit Integralrechnung, lineare Funktion ansehen.
Das Flächenproblem
Schon den alten griechischen Mathematikern war das grundlegende Prinzip zur Bestimmung krummlinig begrenzter Flächen bekannt. Die Differentialrechnung, mit der wir uns schon beschäftigten, wurde jedoch weitaus später (Ende 17. Jh.) von den Naturwissenschaftlern Leibnitz und Newton entwickelt.
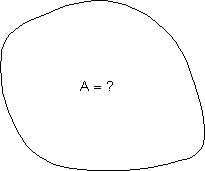
Jede krummlinig begrenzte Fläche lässt sich in endlich viele Flächen zerlegen, in denen nur eine krummlienige Begrenzung auftritt. Alle anderen Begrenzungen sind dann geradlinig.
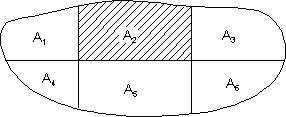
Die einzelnen Teilflächen ( z.B. hier A2 ) können im Kartesischen Koordinatensystem als Fläche zwischen der krummlinigen Begrenzung und der Abszissenachse dargestellt werden.
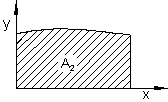
Wenn die krummlinige Begrenzung der Graph einer stetigen Funktion f (x) ist, dann stellt sich die Frage, ob eine Funktion F existiert, die jedem Abszissenwert x0 die Fläche F(x0) zuordnet, wie das im gezeigten Einführungsbeispiel der Fall war.
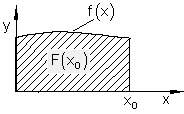

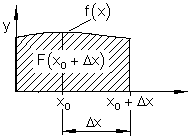
Flächeneinschachtelung
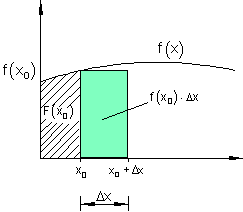
Die gekennzeichnete Fläche unter der Kurve ist etwas kleiner als die tatsächliche.
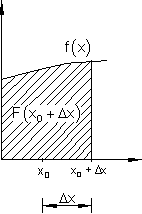
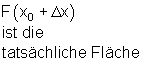
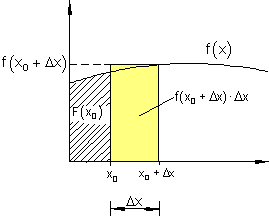
Die gekennzeichnete Fläche unter dieser Kurve ist allerdings etwas größer als die tatsächliche. Je kleiner der Flächenstreifen gemacht wird, desto geringer wird also die Abweichung von der tatsächlichen Fläche.
Mit anderen Worten, mathematisch formuliert:
![]()
![]()
![]()
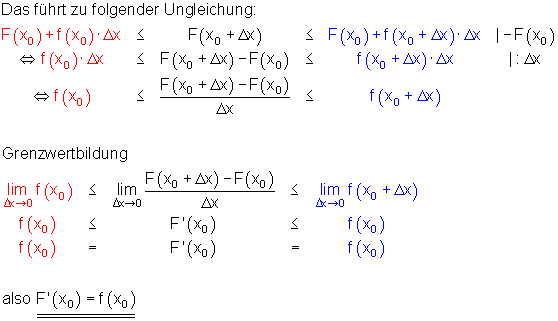

Wenn wir eine Funktion ableiten, sagen wir mit anderen Worten differenzieren, siehe hier. Eine Flächenfunktion zu finden ist offenbar die Umkehrung dieses Vorgangs. Man könnte formal sagen:
Eine Flächenfunktion zu finden, bedeutet aufleiten oder integrieren.
Am Beispiel einer einfachen Potenzfunktion soll im Folgenden intuitiv ein Weg gefunden werden, wie man diese aufleitet, bzw. integriert.
![]()
Definition Ableiten:
Der Exponent wird um eins erniedrigt
Die Potenzfunktion wird mit dem alten Exponenten multipliziert
Aufleiten könnte somit dagegen bedeutet:
Der Exponent wird um eins erhöht
Die Potenzfunktion wird durch den neuen Exponenten dividiert
Das probieren wir im Folgenden aus:
![]()
Definition Stammfunktion:
Man nennt F(x) auch Stammfunktion, denn f(x) erhalten wir durch Ableiten dieser. Das heißt, f(x) stammt von der Funktion F(x) ab.
Das Bestimmen der Stammfunktion nennen wir mit anderen Wortenintegrieren, wir schreiben:

Bis jetzt ist dies eine formale Schreibweise. Nun wollen wir sie mit Leben füllen.
Wir suchen die Stammfunktion
Beispiel
Es ist die Stammfunktion F(x) zu finden, deren Ableitung f(x) = 2x ist.
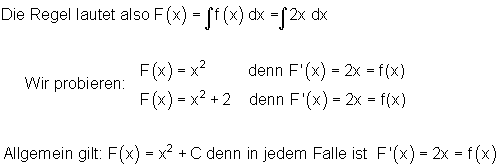
Die beiden Funktionen unterscheiden sich im Absolutglied. Sie haben aber dieselbe Ableitung, weil beim Ableiten das Absolutglied verschwindet. Deshalb müssen wir unsere Regel etwas abändern.
Stammfunktion Regel
Dazu kannst du dir das 📽️Video Integrations Regel, Stammfunktion bilden ansehen.
Die Menge der Stammfunktionen
Das Beispiel zeigt, zu einer Funktion f(x) gibt es nicht nur eine, sondern unendlich viele Stammfunktionen. Sie unterscheiden sich lediglich durch das Absolutglied.
Beispiel
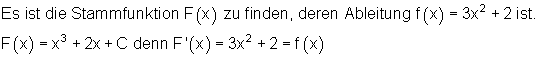
Graphisch lässt sich die Menge aller Stammfunktionen durch eine Kurvenschar einiger Repräsentanten darstellen.
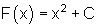
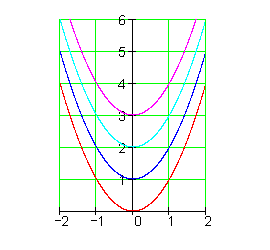
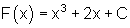
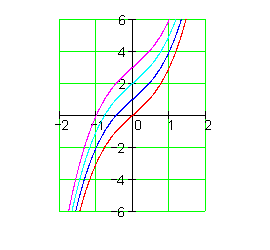
Aufgaben: Stammfunktionen berechnen
Berechne zu folgenden Funktionen f(x) die Stammfunktion F(x). Überprüfe danach Ihr Ergebnis durch Ableiten.
1.
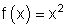
2.
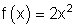
3.
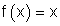
4.
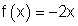
5.
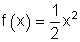
6.
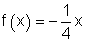
7.
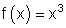
8.
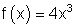
9.
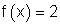
10.
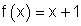
11.
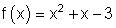
12.
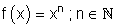
Dazu findest du hier die Lösungen.
Und hier eine Übersicht über weitere Beiträge zum Thema Integralrechnung. Dort auch Links zu weiteren Aufgaben.




