In diesem Beitrag erkläre ich zuerst die Multiplikation eines Vektors mit einer Zahl und definiere die S-Multiplikation. Danach definiere ich parallele Vektoren und Einheitsvektoren und erläutere es anhand von Beispielen und Zeichnungen. Zuletzt definiere ich den Vektorraum und erkläre die Gesetzte im Vektorraum.
Multiplikation eines Vektors mit einer Zahl
Wie wir in den Grundlagen der Mathematik gelernt haben: Ein algebraischer Term der Form 4a bedeutet: 4a = a + a + a + a.
![]()
Diese Schreibweise kann man auch für Vektoren übernehmen.

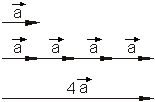

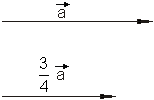
Definition S-Multiplikation:
Wenn k eine positive reelle Zahl und \overrightarrow a ein Vektor ist. Dann versteht man unter k \cdot \overrightarrow a = k \overrightarrow a einen Vektor, der dieselbe Richtung und Orientierung wie \overrightarrow a hat und k-mal so lang wie \overrightarrow a ist.
Weiterhin soll gelten: 0 \overrightarrow a = \overrightarrow 0 (Nullvektor) . Außerdem: -k \overrightarrow a = (-k) \overrightarrow a = - (k \overrightarrow a ) (Gegenvektor von k \overrightarrow a ) .
Die Multiplikation eines Vektors mit einer Zahl nennt man auch S-Multiplikation.
Für diese S-Multiplikation gelten folgende Rechenregeln:
Rechenregel S-Multiplikation:

Einheitsvektoren
Definition parallele Vektoren:
Wir nennen zwei Vektoren (zueinander) parallel (oder kollinear), wenn einer von beiden ein Vielfaches des anderen ist.
Definition Einheitsvektor:
Verwendet man zur Darstellung aller kollinearen (parallelen) Vektoren einen Grundvektor \overrightarrow a mit der Länge 1 (also | \overrightarrow a | = 1 ) , so bezeichnet man diesen als Einheitsvektor \overrightarrow e_a in der Richtung des Vekktors \overrightarrow a .
Die Länge eines Vektors wird auch Betrag des Vektors genannt. Alle Vektoren mit der Länge 1 werden als Einheitsvektoren bezeichnet. Jeder beliebige Vektor lässt sich als Vielfaches seines Einheitsvektors darstellen.
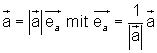
Beispiel 1 Einheitsvektor:
Dies veranschauliche ich anhand einer Zeichnung:

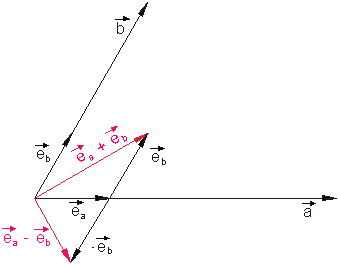
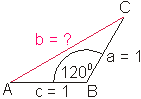
Die Berechnung der Seite b erfolgt mit dem Kosinussatz.
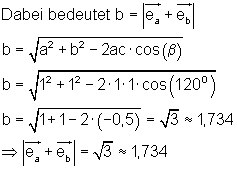
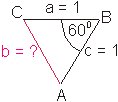
Die Berechnung der Seite b erfolgt mit dem Kosinussatz.
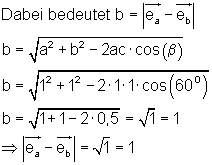
Definition Vektorraum
Ein Vektorraum oder linearer Raum ist eine algebraische Struktur, deren Elemente Vektoren heißen. Diese können addiert oder mit Zahlen (Skalaren) multipliziert werden. Das Ergebnis ist wieder ein Vektor desselben Vektorraums.
In einem reellen Vektorraum V, das ist ein solcher, in dem die Skalare reelle Zahlen sind, gelten folgende Gesetze:
Gesetzte im Vektorraum:

Obige Definition ist auf den reellen Vektorraum beschränkt, da im Folgenden nur in solchen Strukturen gearbeitet wird.
Hier findest du eine Übersicht über alle Beiträge und Aufgaben zum Thema Vektorrechnung.


