Im letzten Beitrag hatte ich die wichtigen Begriffe der Mengenlehre definiert, die Schreibweise und die Darstellungsform vorgestellt. Hier werde ich mich nur mit den Eigenschaften von Mengen beschäftigen. Zuerst stelle ich Kriterien für die Beschreibung von Mengen vor. Danach definiere ich die Begriffe Grundmenge, Obermenge, Teilmenge, Äquivalenz, Mengengleichheit anhand vieler Beispiele. Zuletzt stelle ich den Plausibilitätsbeweis bei Teilmengen vor.
Kriterien für die Beschreibung von Mengen
Indem man Kriterien für die beschreibende Form von Mengen angibt, wählt man die Elemente der zu bestimmenden Menge aus einer umfangreicheren Menge aus.
Beispiel:
A ist die Menge aller natürlichen Zahlen zwischen 1 und 10 und die Elemente sind Quadratzahlen.
A = {x | x ist eine natürliche Zahl \land 1 ≤ x ≤ 10 \land x ist eine Quadratzahl }
B ist die Menge aller natürlichen Zahlen zwischen 1 und 10.
B = {x | x ist eine natürliche Zahl \land 1 ≤ x ≤ 10 }
C ist die Menge der natürlichen Zahlen.
Grundmenge und Obermenge
In dieser Beschreibung treten drei Kriterien auf, die ausgehend von einer Grundmenge ( Menge C ) über eine Obermenge ( Menge B ) zu der zu bestimmenden Menge A führen.
Grundmenge C = { 0; 1; 2; 3; 4; 5; …. }
Obermenge B = { 1; 2; 3; 4; 5; 6; 7; 8; 9; 10 }
A = { 1; 4; 9 }
Bei der Betrachtung der Mengen A, B, C zeigen sich bereits bestimmte Eigenschaften von Mengen:
Die Menge der natürlichen Zahlen hat unendlich viele Elemente. Sie wird im Gegensatz zu den Mengen A und B, die endlich viele Elemente enthalten, als nicht endliche Menge bezeichnet.
Weiterhin kann man erkennen, dass alle Elemente von A in B und C enthalten sind. Und alle Elemente von B sind auch in C enthalten sind. Dieser Sachverhalt wird mit dem Begriff Teilmenge definiert.
Definition Teilmenge
Eine Menge A ist Teilmenge einer Menge B, wenn jedes Element von A auch Element von B ist.
Hier siehst du die mathematische Schreibweise und Beispiele:

Meist werden die Kriterien für Mengen so gewählt, dass ihre Elemente einer Grundmenge entnommen werden, also die zu bestimmende Menge Teilmenge der Grundmenge ist. Da diese Grundmengen in der Mathematik oft Zahlenmengen sind, vereinfacht man die Schreibweise dadurch, dass die Grundmenge als Index der Mengenklammer hinzugeführt wird.
Vergleicht man zwei Mengen miteinander, so ist eine Ordnungsstruktur im Sinne von größer oder kleiner als nicht sinnvoll. Der Vergleich zweier Mengen kann sich daher nur auf andere Eigenschaften beziehen, so z. B. auf die Anzahl der Elemente. Diese Anzahl bezeichnet man als Mächtigkeit der Menge. Die Zahl selbst heißt Kardinalzahl.
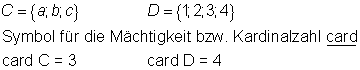
Definition Äquivalenz
Zwei Mengen heißen äquivalent, wenn sie gleichmächtig sind. Das heißt, sie enthalten gleich viele Elemente.
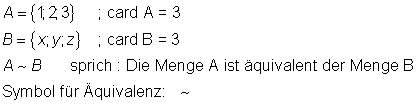
Die Äquivalenz zweier Mengen lässt sich durch Zuordnung der Elemente feststellen.
Bemerkung:
Zwei Mengen A und B sind äquivalent, wenn jedem Element von A genau ein Element von B zugeordnet werden kann und umgekehrt.
Beispiel für die Äquivalenz zweier unterschiedlicher Mengen:
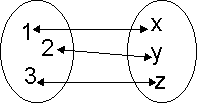
Um die Gleichheit von Mengen festzustellen, muss geprüft werden, ob die beiden Mengen dieselben Elemente enthalten.
Definition Mengengleichheit
Zwei Mengen sind gleich, wenn sie dieselben Elemente enthalten.
Beispiel gleicher Mengen
A = {u; v; w} B = {u; v; w}. Also gilt: A = B
Die Menge A ist gleich der Menge B, da sie dieselben Elemente enthält. Dabei ist die Reihenfolge der Elemente unerheblich. Auch über die Teilmengenbezeichnung kann auf die Gleichheit von Mengen geschlossen werden.
Satz:
Ist die Menge A Teilmenge der Menge B und die Menge B Teilmenge der Menge A, so ist die Menge A gleich der Menge B.
![]()
Plausibilitätsbeweis bei Teilmengen:
A ist Teilmenge von B. Damit ist jedes Element von A auch Element von B.
B ist Teilmenge von A. Damit ist jedes Element von B auch Element von A.
Also sind beide Mengen gleich.
Dazu findest du hier eine Übersicht über alle Beiträge und Aufgaben zum Thema Aussagen und Mengen, darin auch Links zu Aufgaben.


