Hier findest du die Lösungen zu Aufgaben zur Binominalverteilung III, diesmal muss man unter anderem darum Sigma-Umgebungen berechnen.
1.
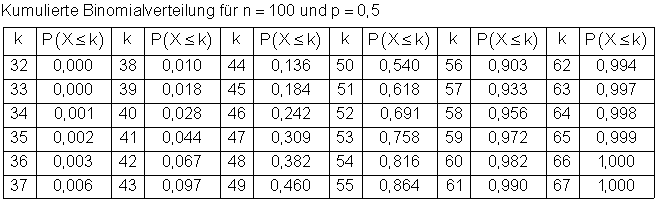
Wir werfen eine Münze 100 mal. Die Wahrscheinlichkeit für Kopf und Zahl ist jeweils p = 0,5. Bestimme die Wahrscheinlichkeit folgender Ereignisse:
A: Wir werfen genau 52 mal Kopf.
B: Wir werfen mindestens 43 mal Kopf.
C: Wir werfen mindestens 38 mal und höchstens 56 mal Kopf.
D: Wir werfen weniger als 45 mal Kopf.
E: Wir werfen mindestens 40 mal und höchstens 60 mal Kopf.
F: Wir werfen mehr als 47 mal Kopf.
G: Wir werfen mindestens 45 mal und höchstens 55 mal Kopf.
H: Wir werfen genau 50 mal die Zahl.
1. Ausführliche Lösungen
A: Genau 52 mal Kopf {0, ……51, 52, 53, ….., 100}
![]()
Die Wahrscheinlichkeit dafür, genau 52 mal Kopf zu werfen ist 0,073.
B: Mindestens 43 mal Kopf {0, …..,42, 43, 44, 45, ….., 100}
![]()
Die Wahrscheinlichkeit dafür, mindestens 43 mal Kopf zu werfen ist 0,933.
C: Mindestens 38 mal und höchstens 56 mal Kopf {0, …..,37, 38,…, 56, 57, ….., 100}
![]()
Die Wahrscheinlichkeit dafür, mindestens 38 mal und höchstens 56 mal Kopf zu werfen ist 0,897.
D: Weniger als 45 mal Kopf {0, 1, …, 44, 45, 46, ….., 100}
![]()
Die Wahrscheinlichkeit dafür, weniger als 45 mal Kopf zu werfen ist 0,136.
E: Mindestens 40 mal und höchstens 60 mal Kopf {0, …..,39, 40,…, 60, 61, ….., 100}
![]()
Die Wahrscheinlichkeit dafür, mindestens 40 mal und höchstens 60 mal Kopf zu werfen ist 0,964.
F: Mehr als 47 mal Kopf {0, …..,47, 48, 49, 50, ….., 100}
![]()
Die Wahrscheinlichkeit dafür, mehr als 47 mal Kopf zu werfen ist 0,691.
G: Mindestens 45 mal und höchstens 55 mal Kopf {0, …..,44, 45,…, 55, 56, ….., 100}
![]()
Die Wahrscheinlichkeit dafür, mindestens 45 mal und höchstens 55 mal Kopf zu werfen ist 0,728.
H: Genau 50 mal Kopf {0, ……49, 50, 51, ….., 100}
![]()
Die Wahrscheinlichkeit dafür, genau 50 mal Kopf zu werfen ist 0,08.
2.
In 50% aller Haushalte in Deutschland sind zwei Autos vorhanden. Für eine Befragung wählen wir 100 Haushalte zufällig aus. Bestimme die Wahrscheinlichkeit folgender Ereignisse:
A: In weniger als 60 Haushalten sind zwei Autos vorhanden.
B: In genau 60 Haushalten sind zwei Autos vorhanden.
C: In mehr als 40 Haushalten sind zwei Autos vorhanden.
D: In mindestens 40 und höchstens 60 Haushalten sind zwei Autos vorhanden.
2. Ausführliche Lösungen
A: In weniger als 60 Haushalten sind zwei Autos vorhanden. {0, 1, …, 59, 60, …, 100}
![]()
Die Wahrscheinlichkeit dafür, dass in weniger als 60 Haushalten zwei Autos vorhanden sind, ist 0,972.
B: In genau 60 Haushalten sind zwei Autos vorhanden {0, ……59, 60, 61, ….., 100}
![]()
Die Wahrscheinlichkeit dafür, dass in genau 60 Haushalten sind zwei Autos vorhanden sind, ist 0,01.
C: In mehr als 40 Haushalten sind zwei Autos vorhanden {0, …..,40, 41, 42, …, 100}
![]()
Die Wahrscheinlichkeit dafür, dass in mehr als 40 Haushalten sind zwei Autos vorhanden sind, ist 0,972.
D: In mindestens 40 und höchstens 60 Haushalten sind zwei Autos vorhanden
{0, …..,39, 40,…, 60, 61, ….., 100}
![]()
Die Wahrscheinlichkeit dafür, dass in mindestens 40 und höchstens 60 Haushalten sind zwei Autos vorhanden sind, ist 0,964.
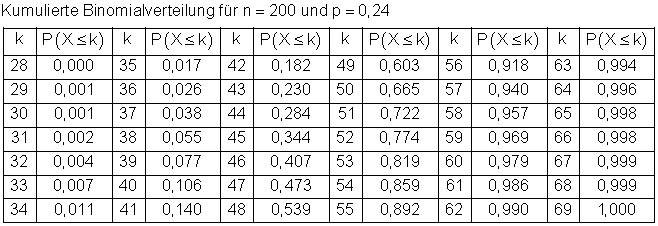
3.
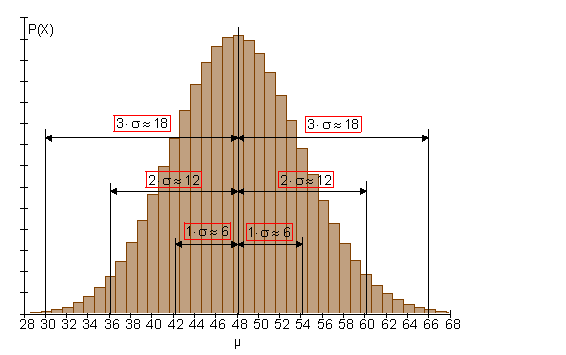
Nebenstehende Grafik zeigt eine Binomialverteilung mit verschiedenen Sigma-Umgebungen.
a) Berechne den Erwartungswert und die Standardabweichung.
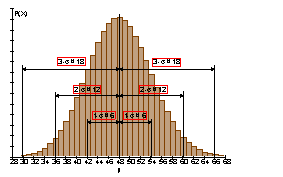
Binomialverteilung für n = 200 und p = 0,24.
b) Berechne die Wahrscheinlichkeit folgender Sigma-Umgebungen:
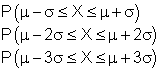
3. Ausführliche Lösungen
a)
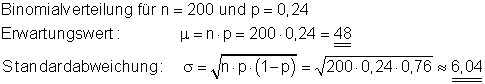
b) Wahrscheinlichkeit der einfachen Sigma- Umgebung.
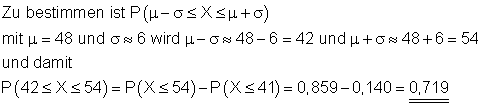
Mit einer Wahrscheinlichkeit von etwa 0,719 (71,9%) liegt die Anzahl der Erfolge im Intervall [ 42 ; 54 ]. Das entspricht etwa der einfachen Sigma- Umgebung vom Erwartungswert.
Wahrscheinlichkeit der doppelten Sigma- Umgebung.
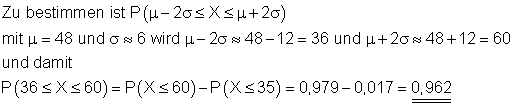
Mit einer Wahrscheinlichkeit von etwa 0,962 (96,2%) liegt die Anzahl der Erfolge im Intervall [ 36 ; 60 ]. Das entspricht etwa der doppelten Sigma- Umgebung vom Erwartungswert.
Wahrscheinlichkeit der dreifachen Sigma- Umgebung.
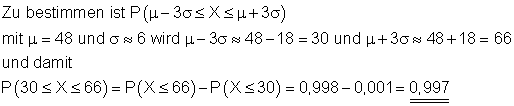
Mit einer Wahrscheinlichkeit von etwa 0,997 (99,7%) liegt die Anzahl der Erfolge im Intervall [ 30 ; 66 ]. Das entspricht etwa der dreifachen Sigma- Umgebung vom Erwartungswert.
4.
Nebenstehende Grafik zeigt eine Binomialverteilung mit verschiedenen Prozent-Umgebungsradien. Wie groß ist jeweils der Radius, der zu einer 90%, 95% bzw. 99% Umgebung gehört?
Drücke den Radius in Einheiten von Sigma aus!
![]()
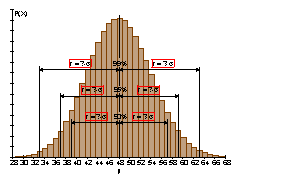
Binomialverteilung fürn = 200 und p = 0,24.
4. Ausführliche Lösungen
Liegt für die Binomialverteilung eine Tabelle mit den kumulierten Wahrscheinlichkeiten vor, lässt sich das Problem durch Einschachtelung lösen.

Ansatz für die 90% Wahrscheinlichkeit mit r = 10.

Der gesuchte Radius liegt zwischen den Werten 9 und 10. Da es sich bei der Binomialverteilung um eine diskrete Verteilung handelt, muss man sich für den Radius entscheiden, der der gewünschten Wahrscheinlichkeit am nächsten liegt. In diesem Fall ist das der Radius r = 9. Teilt man diesen Wert durch Sigma, dann lässt sich der Radius als vielfaches von Sigma darstellen.
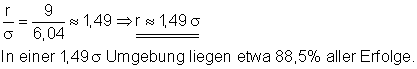
Ansatz für die 95% Wahrscheinlichkeit mit r = 12.

Der gesuchte Radius liegt zwischen den Werten 11 und 12. Der Radius r = 11 liegt der gewünschten Wahrscheinlichkeit am nächsten.
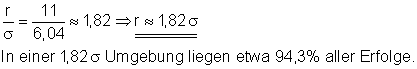
Ansatz für die 99% Wahrscheinlichkeit mit r = 14.

Der gesuchte Radius hat den Wert r = 15
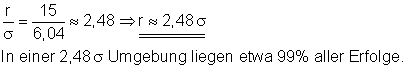
Hier findest du die Aufgaben.
Und hier weitere Aufgaben hierzu: Aufgaben zur Binomialverteilung I
und Aufgaben zur Binomialverteilung II.
Hier findest du eine Übersicht über alle Beiträge zum Thema Wahrscheinlichkeitsrechnung, darin auch Links zu den Aufgaben Binominalverteilung II, IV und V.

