Hier findest du die Lösungen mit komplettem Lösungsweg der Aufgaben zu Gleichungssystemen mit zwei Variablen.
Dabei können dir diese Videos helfen: Playlist aller Videos zu linearen Gleichungen.
1. Bestimme die Lösungsmengen folgender Gleichungssysteme!
a) Ausführliche Lösung mit dem Einsetzverfahren (hier erklärt):
a) (I) 5y - 3x = 1
(II) x = y +1
x in (I) einsetzen:
5y - 3(y + 1) = 1
\Leftrightarrow 5y - 3y - 3 = 1 | +3 \\ \Leftrightarrow 2y = 4 | : 2
\Leftrightarrow \underline{\underline {y = 2}}
y = 2 in (II) einsetzen:
x = 2 + 1
\Leftrightarrow \underline{\underline { x = 3}}
Lösung: L = {(3 | 2)}
Probe:
(I) 5y - 3(y + 1) = 1
\Rightarrow 5 \cdot 2 - 3 \cdot 3 = 1
\Leftrightarrow 10 - 9 = 1 (w)
(II) x = y +1 \\ \Rightarrow 3 = 2 + 1 (w)
b) Ausführliche Lösung mit dem Einsetzverfahren
(I) 4x + 5y = 32
(II) y = 5x - 11
(II) y = 5x - 11 in (I) einsezten:
4x + 5 (5x - 11) = 32 \\ \Leftrightarrow 4x + 25x - 55 = 32 | + 55
\Leftrightarrow 29x = 87 | : 29 \\ \Leftrightarrow \underline{\underline{x = 3}}
x = 3 in (II) einsetzen:
y = 15 -11 \\ \Leftrightarrow \underline{\underline{y = 4}}
Lösung: L = {(3 | 4)}
Probe:
(I) 4x + 5y = 32
\Rightarrow 4 \cdot 3 + 5 \cdot 4 = 32
\Leftrightarrow 12 + 20 = 32 (w)
(II) y = 5x - 11
\Rightarrow 4 = 5 \cdot 3 - 11
\Leftrightarrow 4 = 15 - 11 (w)
c) Ausführliche Lösung mit dem Einsetzverfahren
(I) 15y - 4x = -50
(II) x = y + 7
(II) x = y + 7 in (I) einsetzen
15y - 4(y + 7) = -50
\Leftrightarrow 15y - 4y - 28 = -50 | + 28 \\ \Leftrightarrow 11y = -22 | :11
\Leftrightarrow \underline{\underline{y = -2}}
y = -2 in (II) einsetzen:
x = -2 + 7
\Leftrightarrow \underline{\underline{x = 5}}
Lösung: L = {( 5 | -2)}
Probe: (I) 15y - 4x = -50
\Rightarrow 15 \cdot (-2) - 4 \cdot 5 = -50
\Leftrightarrow -30 - 20 = -50 (w)
(II) x = y + 7
\Rightarrow 5 = -2 + 7 (w)
d) Ausführliche Lösung mit dem Gleichsetzverfahren (hier erklärt):
(I) 3x = y + 15 | -15
(II) 2y - 10 = 2x | + 10
————————————
(I) 3x - 15 = y
(II) 2y = 2x + 10 | :2
————————————
(I) y = 3x - 15
(II) y = x + 5
Jetzt setze ich die rechte Seite gleich:
3x - 15 = x + 5 | - x
\Leftrightarrow 2x - 15 = 5 | + 15 \\ \Leftrightarrow 2x = 20 | : 2
\Leftrightarrow \underline{\underline{x = 10}}
x = 10 einsetzen in (II) y = x + 5
y = 10 + 5 \\ \Leftrightarrow \underline{\underline{y = 15}}
Lösung: L = {(10 | 15)}
Probe:
(I) 3x = y + 15
\Rightarrow 3 \cdot 10 = 15 + 15 \\ \Leftrightarrow 30 = 30 (w)
(II) 2y - 10 = 2x
\Rightarrow 2 \cdot 15 -10 = 2 \cdot 10 \\ \Leftrightarrow 30 - 10 = 20 (w)
2. Bestimme die Lösungsmengen folgender Gleichungssysteme
a) Ausführliche Lösung mit dem Additionsverfahren (hier erklärt und mit anderen Werten kannst du dir in diesem  Video Additionsverfahren: Lineare Gleichungen lösen ansehen.):
Video Additionsverfahren: Lineare Gleichungen lösen ansehen.):
(I) 2y = 2x - 40 | -2x
(II) 3x = 10 - 2y | +2y
————————————
(I) 2y -2x = - 40
(II) 2y + 3x = 10 | \cdot (-1)
————————————
(I) 2y - 2x = -40
(II) -2y - 3x = -10
————————————
Jetzt können wir die beiden Gleichungen addieren:
-5x = -50 |: (-5)
\Leftrightarrow \underline{\underline{x = 10}}
Als nächstes setzen wir x = 10 in (I) ein:
2y = 2 \cdot 10 - 40
\Leftrightarrow 2y = 20 - 40 \\ \Leftrightarrow 2y = -20 | :2
\Leftrightarrow \underline{\underline{y = -10}}
Lösung: L = {(10 | -10)}
Probe:
(I) 2y = 2x - 40
\Rightarrow 2 \cdot (-10) = 2 \cdot 10 -40\\ \Leftrightarrow -20 = 20 - 40
\Leftrightarrow -20 = -20 (w)
(II) 3x = 10 - 2y
\Rightarrow 3 \cdot 10 = 10 - 2 \cdot (-10)
\Leftrightarrow 30 = 10 + 20 <=> 30 = 30 (w)
b) Ausführliche Lösung mit dem Gleichsetzverfahren (hier erklärt):
(I) \frac{x}{2} - \frac{3y}{5} = 3 | + \frac{3y}{5}
(II) \frac{x}{4} + y = 8 | -y
————————————
(I) \frac{x}{2} = \frac{3y}{5} + 3
(II) \frac{x}{4} = 8 - y | \cdot 2
————————————
(I) \frac{x}{2} = \frac{3y}{5} + 3
(II) \frac{x}{2} = 16 - 2y
Jetzt können wir die reche Seite gleichsetzen:
\frac{3y}{5} + 3 = 16 - 2y | + 2y
\Leftrightarrow \frac{3y}{5} + 2y + 3 = 16 | -3 \\ \Leftrightarrow \frac{3y}{5} + \frac{10y}{5} = 13 | \cdot 5 \\ \Leftrightarrow 3y + 10 y = 65 \\ \Leftrightarrow 13y = 65 | : 13 \\ \Leftrightarrow \underline{\underline{y = 5}}
y = 5 einsetzen in (II) \frac{x}{2} = 16 - 2y
\Rightarrow \frac{x}{2} = 16 - 10
\Leftrightarrow \frac{x}{2} = 6 | \cdot 2 \\ \Leftrightarrow \underline{\underline{x = 12}}
Lösung: L = {(12 | 5)}
Probe:
(I) \frac{x}{2} = \frac{3 \cdot y}{5} + 3
\Rightarrow \frac{12}{2} = \frac{3 \cdot 5}{5} + 3 \\ \Leftrightarrow 6 = 3 + 3 (w)
(II) \frac{x}{4} = 8 - y
\Rightarrow \frac{12}{4} = 8 - 5
\Leftrightarrow 3 = 3 (w)
c) Ausführliche Lösung mit dem Additionsverfahren
Das Additionsverfahren mit anderen Werten kannst du dir in diesem 
d) Ausführliche Lösung mit dem Additionsverfahren
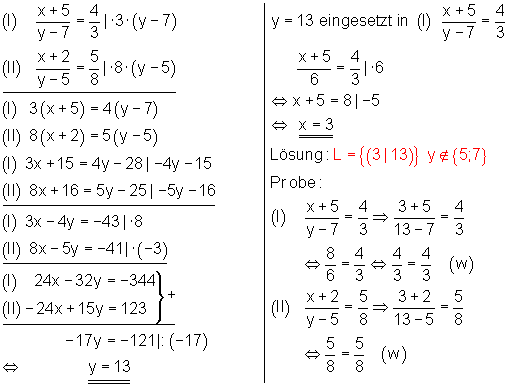
3. Bestimmen Sie die Lösungsmengen folgender Gleichungssysteme
a) Ausführliche Lösung mit dem Additionsverfahren
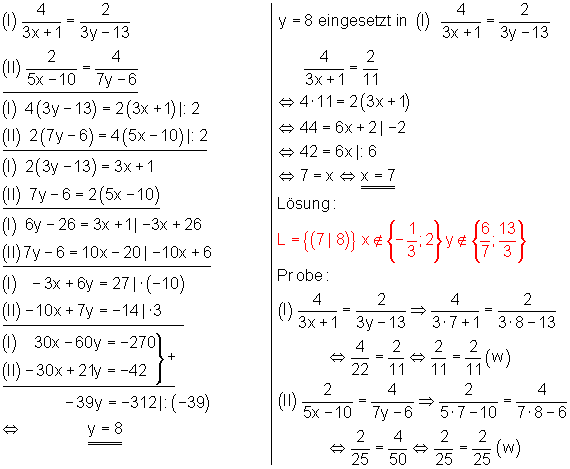
b) Ausführliche Lösung mit dem Additionsverfahren

c) Ausführliche Lösung mit dem Additionsverfahren
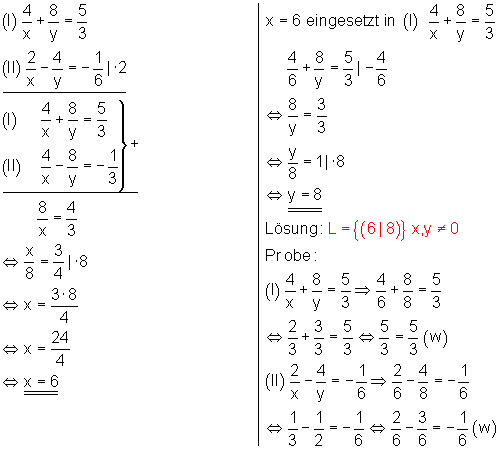
d) Ausführliche Lösung mit dem Additionsverfahren
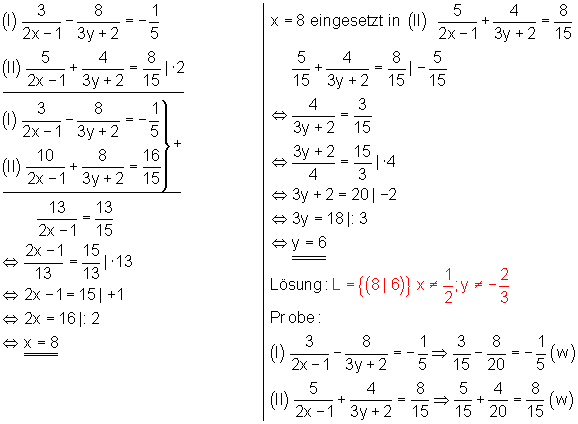
4. Bestimme die Lösungsmenge des Gleichungssystems
Ausführliche Lösung mit dem Additionsverfahren
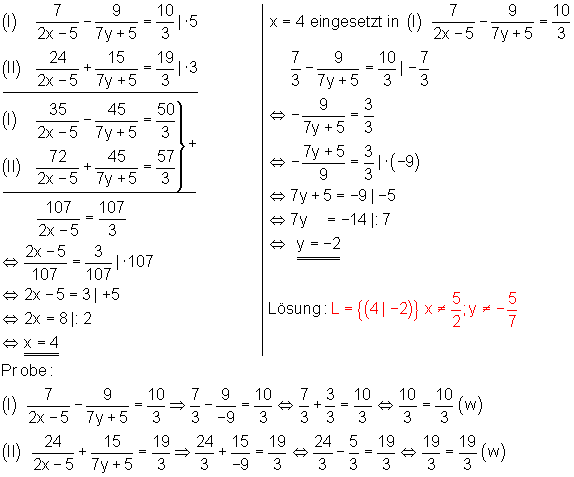
5. Vater und Sohn
Ein Vater ist im Augenblick viermal so alt wie sein Sohn und wird in 5 Jahren nur noch dreimal so alt sein. Wie alt sind beide zum jetzigen Zeitpunkt?
Ausführliche Lösung Variablen: Vater x Sohn y
Ein Vater ist im Augenblick viermal so alt wie sein Sohn x = 4y
Vater ist in 5 Jahren nur noch dreimal so alt wie sein Sohn x + 5 = 3( y + 5 )
Gleichungssystem:
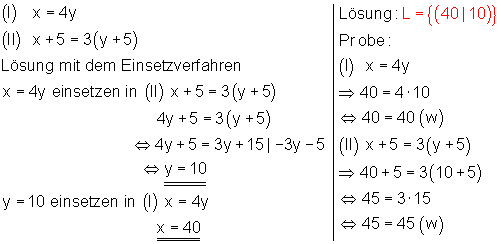
Der Vater ist 40, der Sohn 10 Jahre alt.
6. Behälter füllen
In welcher Zeit wird ein Behälter von zwei Leitungen halb gefüllt, wenn die erste Leitung zur Füllung des gesamten Behälters 18 min und die zweite dazu 22 Minuten benötigt?
Ausführliche Lösung Ansatz:
Die erste Leitung füllt den Behälter in einer Minute 1/18.
Die zweite Leitung füllt den Behälter in einer Minute 1/22.
Gesucht ist die Zeit in Minuten, also die Variable x.
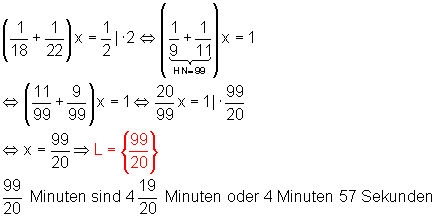
Der Behälter wird in 4 Minuten und 57 Sekunden halb gefüllt.
Die Aufgabe ließ sich mit einer einfachen Gleichung lösen.
7. Der Umfang eines Rechtecks beträgt 180 cm.
Wie lang ist die Seite a, wenn die Seite b 30 cm lang ist?
Ausführliche Lösung Umfang des Rechtecks
2a + 2b = 180
Seite b ist 30 cm lang
b=30
Gleichungssystem

Die Seite a ist 60 cm lang.
8. Quersumme
Die Quersumme einer zwei zifferigen Zahl ist 9. Stellt man die Ziffern um, so ist die neue Zahl 7/4 mal so groß wie die alte. Wie heißen die beiden Ziffern?
Ausführliche Lösung:
Die Zahl besteht aus den Ziffern x und y und hat den Wert 10x + y
Die Quersumme der Zahl ist x + y = 9
Stellt man die Ziffern um, so erhält man die neue Zahl mit dem Wert 10y + x
Die neue Zahl ist 7/4 mal so groß wie die alte 10y + x = 7/4( 10x + y )
Das Gleichungssystem lautet :
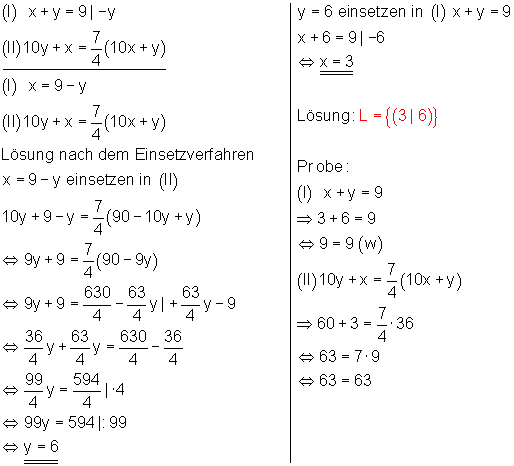
Die Ziffern der Zahl heißen 3 und 6. Die Zahl lautet 36.
Die Aufgaben hierzu sind hier.
Die Theorie hierzu findet ihr hier: Lineare Gleichungssysteme mit 2 Gleichungen und 2 Variablen.
Und hier eine Übersicht über alle Beiträge zum Thema Gleichungen, darin Links zu weiteren Aufgaben.


