Hier findest du die Lösungen der Aufgaben zur Differenzialrechnung zur Vorbereitung der Klassenarbeit I mit komplettem Lösungsweg.
1. Ausführliche Lösung
a)
Mit den drei Punkten stellen wir drei Gleichungen mit drei Variablen auf. Dann lösen wir dies mit nach Gauss. Dazu kannst du dir das Video 📽️Video Gauss-Algorithmus 3 Gleichungen mit 3 Variablen lösen ansehen.
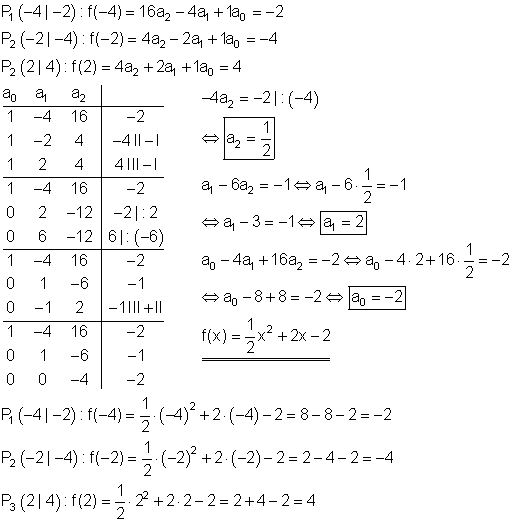
b) Der Scheitelpunkt der Parabel ist ein Extrempunkt.
Dazu kannst du dir diese Videos ansehen:
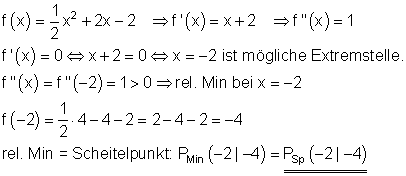
c)
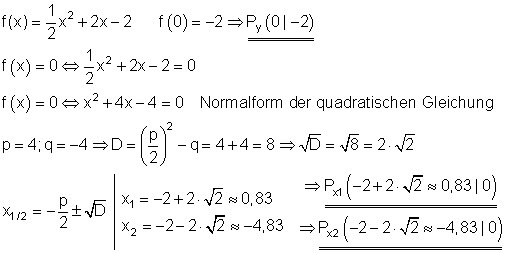
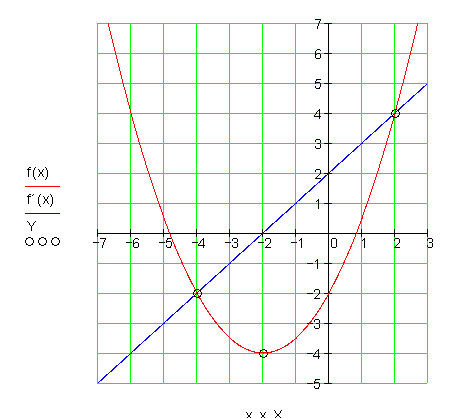
d)
2.
Was verstehest du unter der Steigung eines Funktionsgraphen in einem Punkt?
Ausführliche Lösung
Bei einer linearen Funktion ist die Steigung in jedem Punkt des Graphen gleich. Sie lässt sich leicht über das Steigungsdreieck berechnen. Funktionen mit gekrümmten Grapen haben fast überall unterschiedliche Steigungen. Über das Steigungsdreieck lässt sich die mittlere Steigung, die Sekantensteigung bestimmen, repräsentiert durch den Differenzenquotienten. Erst die Grenzwertbildung führt von der Sekanten- zur Tangentensteigung. Deshalb ist die Steigung eines Funktionsgraphen in einem Punkt gleich der Steigung der Tangente in diesem Punkt. Man nennt sie auch momentane Änderungsrate.
3.
Beschreibe anschaulich (Skizze) und mit Worten, wie man bei einem Graphen von der Sekantensteigung zur Tangentensteigung gelangt.
Ausführliche Lösung
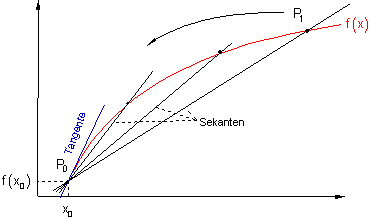
Verbindet man zwei Punkte eines gekrümmten Graphen durch eine Gerade, so bildet diese die Sekante. Die Sekante stellt die mittlere Steigung des Graphen zwischen diesen beiden Punkten dar. Man sagt dazu auch mittlere Änderungsrate. Will man näherungsweise die Steigung in einem Punkt bestimmen, so müssen die beiden Sekantenpunkte möglichst nahe zusammenliegen. Sie dürfen aber nicht aufeinanderliegen. Bewegt man nun den Punkt P1 immer weiter auf P0 zu, so ändert sich die Sekantensteigung. Je mehr man sich dem Punkt P0 nähert, desto mehr nähert sich die Sekantensteigung der Tangentensteigung. Erst der Grenzübergang liefert den genauen Wert der Tangentensteigung. Diese repräsentiert die momentane Änderungsrate.
4.
Welche Bedeutung hat die erste Ableitung einer Funktion an der Stelle x0?
Ausführliche Lösung
Die erste Ableitung einer Funktion an der Stelle x0 ist die Steigung der Tangente im Punkt P ( x0 | f(x0) ) und somit auch die Steigung des Graphen von f(x) in diesem Punkt. Man sagt dazu auch momentane Änderungsrate an der Stelle x0.
5.
Warum nennt man die Ableitungsfunktion auch Steigungsfunktion?
Ausführliche Lösung
Die erste Ableitung einer Funktion an der Stelle x0 ist die Steigung des Graphen von f(x) an dieser Stelle. Da eine stetige Funktion an fast jeder Stelle ableitbar ist, bilden die Ableitungswerte wiederum eine Funktion, die sogenannte Ableitungsfunktion f'(x). f'(x) heißt deshalb auch Steigungsfunktion, weil sie in jedem Punkt die Steigung von f(x) repräsentiert.
6.
a) Ausführliche Lösung
![]()
Die Ableitung einer Konstanten Funktion ist Null. Damit sind auch alle weiteren Ableitungen Null.
6. b) Ausführliche Lösung
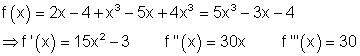
Es ist sinnvoll vor dem Ableiten den Funktionsterm zu vereinfachen.
c) Ausführliche Lösung
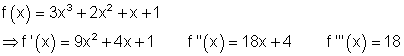
6.d) Ausführliche Lösung

e) Ausführliche Lösung
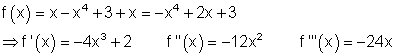
Es ist sinnvoll vor dem Ableiten den Funktionsterm zu vereinfachen.
6. f) Ausführliche Lösung
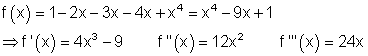
Es ist sinnvoll vor dem Ableiten den Funktionsterm zu vereinfachen.
6. g) Ausführliche Lösung
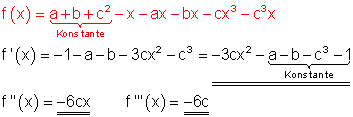
h) Ausführliche Lösung
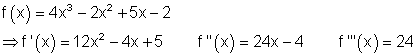
6. i) Ausführliche Lösung
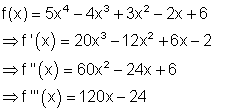
6. j) Ausführliche Lösung

7. Ausführliche Lösung

Alternativlösung mittels Formel:
Tangente und Normale an den Graphen von f(x) durch die Punkte P( x0 | f(x0) )

8. Ausführliche Lösung
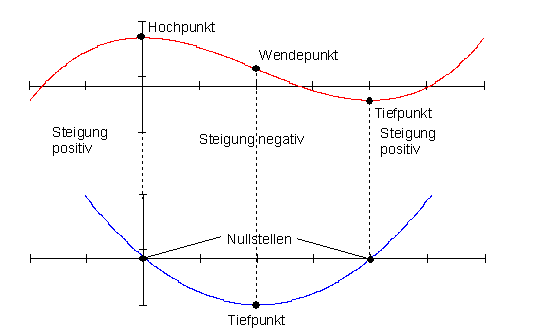
Markante Punkte des Graphen von f(x) sind Hochpunkt, Tiefpunkt und der Wendepunkt. Dort, wo f(x) den Hoch- bzw. Tiefpunkt hat, ist der Wert der Ableitungsfunktion Null, da sich an dieser Stelle von f(x) waagerechte Tangenten befinden. Waagerechte Tangente an f(x) bedeutet Steigung von f(x) an diesen Stellen Null. Die Steigung im Wendepunkt ist negativ aber maximal im Intervall zwischen den Extrempunkten. Deshalb hat dort die Ableitungsfunktion ihren Tiefpunkt. Die Funktionswerte der Ableitungsfunktion sind zwischen ihren Nullstellen negativ, außerhalb dieser positiv. Das entspricht genau der Steigung von f(x).
Hier findest du die Aufgaben.
Die Theorie findest du hier: Von der Sekantensteigung zur Tangentensteigung.
Hier eine Übersicht über alle Beiträge zur Differentialrechnung. Dort sind auch Links zu weiteren Aufgaben und Theorieteilen.

