Hier findest du Aufgaben und Lösungen zur Volumenberechnung.
Ich stelle zuerst die Formel zur Volumenberechnung vor. Dann zeige ich jeweils anhand eines Beispiels, wie dies bei den einzelnen Körpern berechnet wird und verdeutliche dies mit einer Zeichnung. Danach können Sie eine Aufgabe lösen, ganz am Ende finden Sie die ausführlichen Lösungen.
Für gleichmäßig geformte Körper, gilt:
(Gleichmäßig geformete Körper sind solche, bei denen die Grundfläche durch den ganzen Körper bewegt werden kann.)
Volumen = Grundfläche \cdot Höhe
V = G \cdot h
Würfel
Beispiel:
gegeben: Kantenlänge a = 4cm
gesucht: Volumen
V = A \cdot h
A = a^2
h = a
V = a^2 \cdot a = a^3
\Rightarrow V = 4cm \cdot 4cm \cdot 4cm = \underline{\underline{64cm^3}}
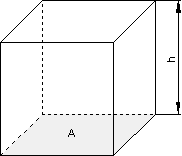
Aufgabe 1 Volumenberechnung Würfel:
Berechne das Volumen für a = 3,75cm !
Quader
Beispiel:
gegeben: a = 3cm, \, b = 4cm, \, c = 2,5cm
gesucht: Volumen
V = A \cdot h
A = a \cdot b
h = c
V = a \cdot b \cdot c
\Rightarrow V = 3cm \cdot 4cm \cdot 2,5cm = \underline{\underline{30cm^3}}
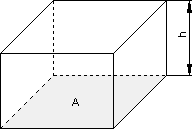
Aufgabe 2 Volumenberechnung Quader:
Berechne das Volumen für a = 4,5cm, \, b = 2,4cm, \, c = 1,5cm
Prisma
Beispiel:
gegeben: a = 3m, \, b = 2m, \, c = 6m
gesucht: Volumen
V = A \cdot h
A = \frac{a \cdot b}{2}
h = c
V = \frac{a \cdot b}{2} \cdot c
\Rightarrow V = \frac{3m \cdot 2m}{2} \cdot 6m = \underline{\underline{18m^3}}
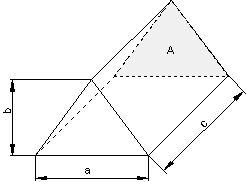
Aufgabe 3 Volumenberechnung Prisma:
Berechne das Volumen für a = 4,5cm, \, b = 2,4cm, \, c = 15cm
Zylinder
Beispiel:
gegeben: d = 40mm, \, L = 2m
gesucht: Volumen in cm^3
V = A \cdot h
A = \frac{d^2 \cdot \pi}{4}
h = L
V = \frac{d^2 \cdot \pi}{4} \cdot L
\Rightarrow V = \frac{4cm \cdot 4cm \cdot \pi}{4} \cdot 200cm = \underline{\underline{2513,274cm^3}}

Achtung: Hier musst du erst Meter in Zentimeter umrechnen! Hier findest du eine Tabellen zum Umrechnen von Zehnerpotenzen, Längen, Flächen, Volumen mit Übungsaufgaben und Lösungen.
Aufgabe 4 Volumenberechnung Zylinder:
Berechne das Volumen für d = 25cm, \, L = 1,75m
Lösungen
Lösung 1 Volumenberechnung Würfel:
Berechne das Volumen eines Würfels für a = 3,75cm
gegeben: Kantenlänge a = 3,75cm
gesucht: Volumen
V = A \cdot h
A = a^2
h = a
V = a^2 \cdot a = a^3 \Rightarrow V = 3,75cm \cdot 3,75cm \cdoz 3,75cm \approx \underline{\underline{52,734cm^3}}
Lösung 2 Volumenberechnung Quader:
Berechne das Volumen eines Quaders für a = 4,5cm, \, b = 2,4cm, \, c = 1,5cm !
gegeben: a = 4,5cm, \, b = 2,4cm, \, c = 1,5cm
gesucht: Volumen
V = A \cdot h
A = a \cdot b
h = c
V = a \cdot b \cdot c \Rightarrow V = 4,5cm \cdot 2,4cm \cdot 1,5cm = \underline{\underline{16,2cm^3}}
Lösung 3 Volumen eines Prismas
Berechne das Volumen eines Prismas für a = 4,5cm, \, b = 2,4cm, \, c = 15cm !
gegeben: a =4,5cm, \, b = 2,4cm, \, 15cm
gesucht: Volumen
V = A \cdot h
A = \frac{a \cdot b}{2}
h = c
V = \frac{a \cdot b}{2} \cdot c \Rightarrow V = \frac{4,5cm \cdot 2,4cm}{2} \cdot 15cm = \underline{\underline{81cm^3}}
Lösung 4 Volumen eines Zylinders
Berechne das Volumen eines Zylinders für d = 25cm, \, L= 1,75m
gegeben: d = 25cm, \, L = 1,75m = 175cm
gesucht: Volumen in cm^3
V = A \cdot h
A = \frac{d^2 \cdot \pi}{4}
h = L
V = \frac{d^2 \cdot \pi}{4} \cdot L
\Rightarrow V = \frac{25cm \cdot 25cm \cdot \pi}{4} \cdot 175cm \approx \underline{\underline{85902,924cm^3}}
Und hier eine Übersicht über weitere Beiträge zum Thema Geometrie.

