Hier findest du die Lösungen der Aufgaben zum Schnittpunkt zweier Geraden. Zuerst (im ersten Teil) sind die beiden Funktionsgleichungen bekannt. Danach (im zweiten Teil) eine Funktionsgleichung und ein Punkt der anderen Geraden. Dabei liegen die Geraden dann senkrecht zueinander.
1. Teil: Funktionsgleichungen bekannt
Gegeben sind die Funktionsgleichungen zweier Geraden g1(x) und g2(x).
Berechne den Schnittpunkt beider Geraden. Zeichne danach die Geraden in ein Koordinatensystem.
Tipps zum Vorgehen hierbei findest du in den Aufgaben.
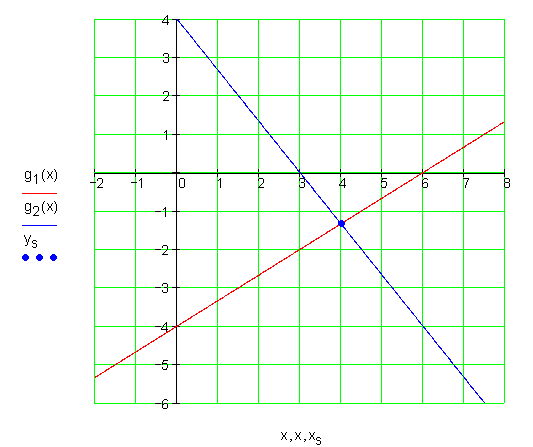
1 .Aufgabe
g_1(x) = \frac{1}{2}x + 2 \quad ; \quad g_2(x) = - \frac{1}{2}x + 4
Ausführliche Lösung:
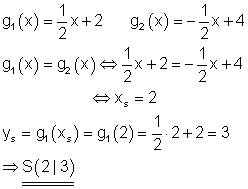
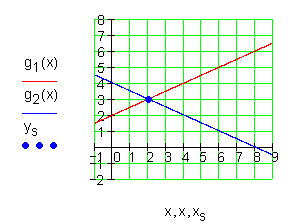
2. Aufgabe
g1(x) = 2x – 1 ; g2(x) = – 2x + 1
Ausführliche Lösung

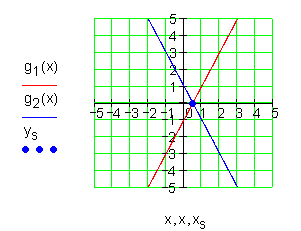
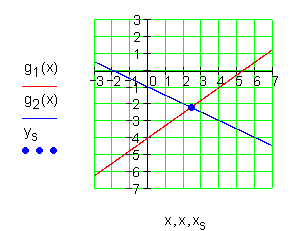
3. Aufgabe
![]()
Ausführliche Lösung
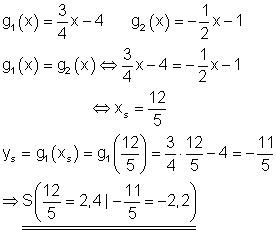
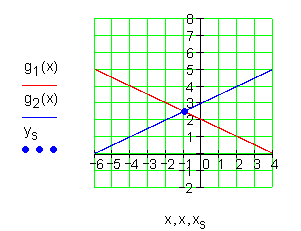
4. Aufgabe
![]()
Ausführliche Lösung
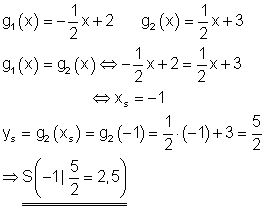
5. Aufgabe
![]()
Ausführliche Lösung
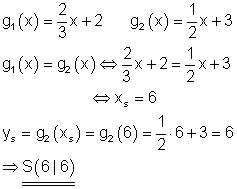
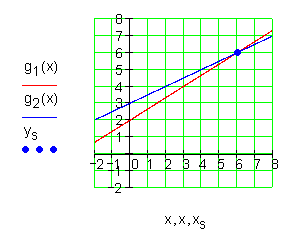
2. Teil: Eine Funktionsgleichung und ein Punkt der anderen Geraden
Gegeben ist die Funktionsgleichung einer Geraden g1(x) und der Punkt P1 , der durch eine andere Gerade verläuft. Beide stehen senkrecht zueinander.
Bestimme die Funktionsgleichung der zu g1(x) senkrecht verlaufenden Geraden, wenn diese durch den Punkt P1 verläuft. Berechne danach die Funktionsgleichung der zweiten Geraden. Zeichne schließlich beide Geraden in ein Koordinatensystem.
Tipps zum Vorgehen hierbei findest du auch in den Aufgaben.
6. Aufgabe
![]()
Ausführliche Lösung
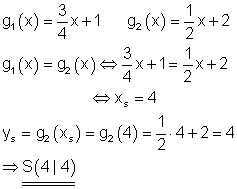
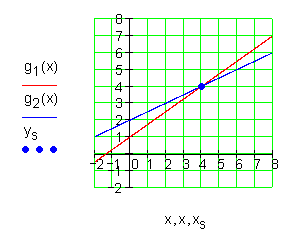
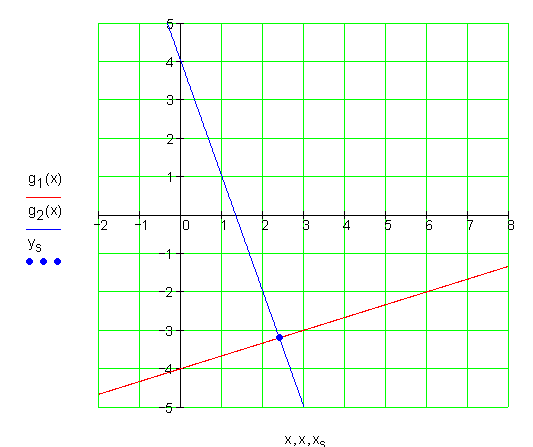
7. Aufgabe
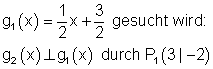
Ausführliche Lösung
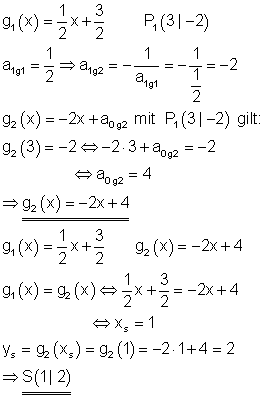
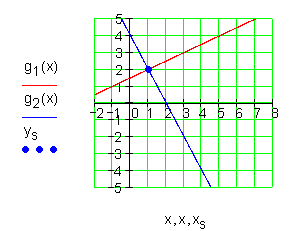
8. Aufgabe

Ausführliche Lösung
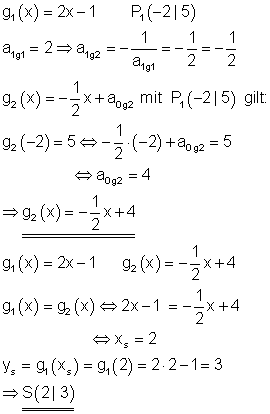
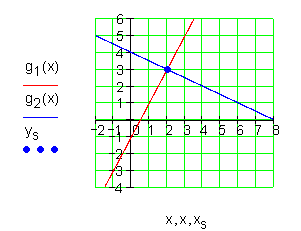
9. Aufgabe
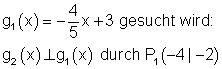
Ausführliche Lösung
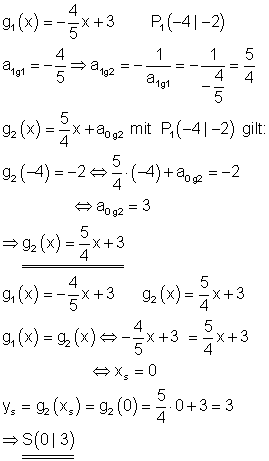
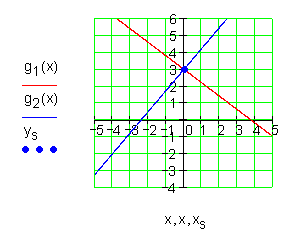
10. Aufgabe
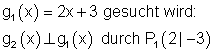
Ausführliche Lösung
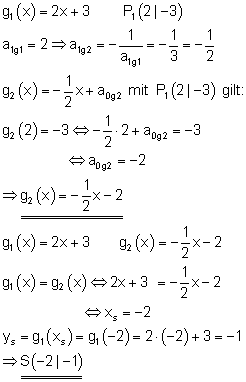
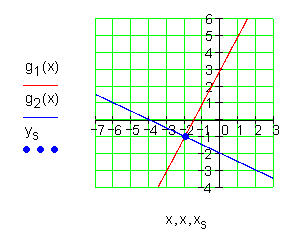
Hier findest du die Aufgaben hierzu.
Außerdem hier weitere Aufgaben Lineare Funktionen Aufgaben V Schnittpunkte mehrerer Geraden.
Hier findest du eine Übersicht über weitere Beiträge zu linearen Funktionen, darin auch Links zu weiteren Aufgaben.

