Hier findet ihr Textaufgaben zu lineare Funktionen. Nachdem ich im vorherigen Beiträgen erklärt habe, wie man die Lage zweier Geraden berechnet, zeige ich hier anhand einiger Beispiele, wie man alltägliche Probleme mittels linearer Funktionen lösen kann.
Tipps zum Vorgehen beim Lösen von Textaufgaben zu linearen Funktionen
Wie bei allen Textaufgaben frage dich als erstes:
- Welche Daten habe ich?
- Nach welchen wird gefragt?
- Wie bringe ich beides in einer Funktionsgleichungen zusammen?
Textaufgabe zu linearen Funktionen 1
Tobias und Mario arbeiten als Krankenpfleger in einer Rehabilitationsklinik und beziehen das gleiche Grundgehalt. Zur Zeit müssen beide viel Überstunden leisten. Am Monatsende vergleichen sie ihre Gehaltsabrechnungen. Dabei stellen sie folgendes fest:
Der Bruttolohn von Tobias beträgt 3559 €. Dafür hat er in diesem Monat 43 Überstunden geleistet.
Der Bruttolohn von Mario dagegen beträgt 3223 €. Dafür hat er nur 27 Überstunden geleistet.
Berechne das Grundgehalt und die Überstundenpauschale!
Was haben wir?
Bruttolohn Tobias 3559 € – 43 Überstunden.
Bruttolohn Mario 3223 € – 27 Überstunden.
Was suchen wir?
Grundgehalt und Überstundenpauschale
Ansatz:
Wir setzen zuerst für die Anzahl der Überstunden x ein. Weil der ausgezahlter Bruttolohn von der Anzahl der Überstunden abhängt: f(x).
Aus Tobias Werten 43 Überstunden und 2559 € Gehalt ergibt sich also P1. Aus Marios Werten P2. Damit können wir anschließend rechnen:
Das Grundgehalt beträgt folglich 2656 €, die Überstundenpauschale 21 €.
Dazu kannst du dir dieses Video📽️ Lineare Funktion Textaufgabe Gehalt ansehen. Anfangs bis zur 3. Minute erkläre ich, wie man ganz einfach den Ansatz in einer Textaufgabe findet. Danach zeige ich, wie man mit den zwei Punkten die Steigung berechnet.
Textaufgabe zu linearen Funktionen 2
Ein Energieversorgungsunternehmen bietet seinen Kunden folgende Stromtarife an:
Eine kWh kostet 0,14 € bei einer monatlichen Grundgebühr von 7,50 €.
a) Stelle einen Funktionsterm auf!
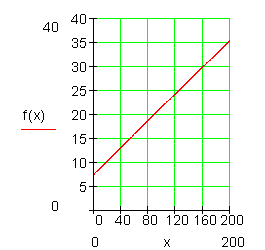
Zeichne den Graphen für die Abnahme bis zu 200 kWh in eingeeignetes Koordinatensystem.
b) Die Stromrechnung für 4 Monate beläuft sich auf 150,40 €.
Wie viel kWh wurden bezogen?
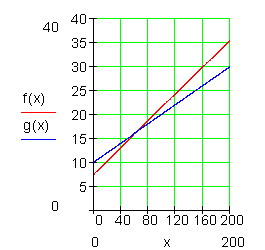
c) Ein Zweitanbieter verkauft Strom für 0,10 € pro kWh bei einer monatlichen Grundgebühr von 10 €.
Ab welcher Abnahme lohnt sich der Wechsel des Stromanbieters?
Lösung:
a) Je mehr kWh verbraucht werden, desto mehr muss mal bezahlen. Deshalb wird x mit 0,14 multipliziert.
Die 7,50 Grundgebühr werden immer auf der Rechnung addiert. Daraus erstellen wir den Term:
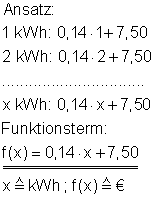
Bemerkung:
Die Rechnung erfolgt ohne Einheiten, diese werden den jeweiligen Ergebnissen angefügt.
b)
c)
Bei einem monatlichen Energiebezug von mehr als 62,5 kWh ist Anbieter II also günstiger als Anbieter I.
Auch dazu kannst du dir ein Video📽️ Lineare Funktion Textaufgabe Strom ansehen.
Textaufgabe zu linearen Funktionen 3
Zur Versorgung der Futterautomaten im Zoo „Koalabär“ benötigt der Tierpfleger täglich 7,5 kg Tierfutter. Zwölf Tage nachdem das Futterlager zum letzten Mal aufgefüllt wurde, befinden sich dort noch 250 kg.
a) Stelle eine Funktionsgleichung auf, die diesen Sachverhalt beschreibt.
b) Auf welche Menge wurde das Futterlager vor zwölf Tagen aufgefüllt?
c) Bei einem Lagerbestand von 50 kg wird der Bestand wieder auf die unter b) berechnete Menge aufgestockt. Wann ist das erforderlich?
Lösung:
a) Funktionsgleichung:
Weil pro Tag 7,5 kg Futter gefressen wird, multiplizieren wir x mit 7,5. Deshalb beschreibt die x-Achse die Zeit in Tagen. Die y-Achse dagegen den Futterbestand in kg. Die Futtermenge vor 12 Tagen kennen wir nicht, deshalb wird der Wert von a mit 0 beschreiben. Wir kennen aber einen Punkt und zwar f(12) = 250.
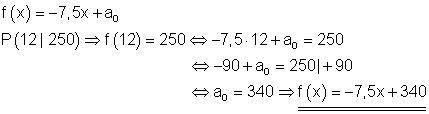
b) Menge vor 12 Tagen
Der Auffüllzeitpunkt liegt bei x = 0.
Der Futterbestand wurde folglich vor 12 Tagen auf 340 kg aufgefüllt.
c) Lagerbestand
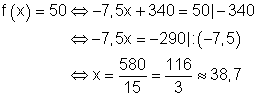
Nach etwa 38,7 Tagen ist das Futterlager also wieder aufzufüllen.
Textaufgabe zu linearen Funktionen 4
Der Telefondienst „Handybillig“ (HB) bietet folgenden Handytarif an: (Das Beispiel ist schon älter, aber noch gut zum Lernen!)
Jede Gesprächsminute kostet 0,06 €, bei einer monatlichen Grundgebühr von 8,50 €.
Die Konditionen von „Handypreiswert“ dagegen (HP) lauten:
Jede Gesprächsminute kostet 0,08 €, bei einer monatlichen Grundgebühr von 5 €.
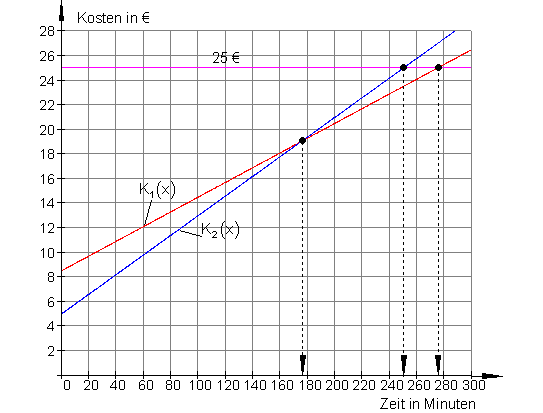
Fertige dazu eine Skizze an!
a) Bei wie viel Minuten sind die Kosten bei beiden gleich?
b) Dir stehen 25 € monatlich zum Telefonieren zur Verfügung (Deine Oma zahlt . 😉
Welchen Dienst wählst du? Wie lange kannst du bei dem gewählten Anbieter telefonieren?
c) Stelle die Ergebnisse von a) und b) im Koordinatensystem dar!
Lösung:
Die Kosten pro Gesprächsminute werden mit x multipliziert, die Grundgebühr addiert. Danach setzen wir die beiden Gleichungen gleich. Dadurch können wir x berechnen. Schließlich setzen wir x in die Gleichungen ein.
a) Wann sind die Kosten gleich?
Nach 175 Minuten herrscht also Kostengleichheit (19 €).
b) Du hast 25
Hier setzen wir beide Gleichungen = 25. Dadurch können wir x, also die Anzahl Minuten berechnen.-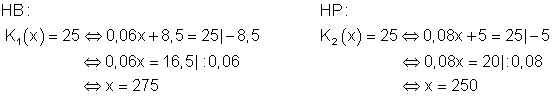
Der Dienst von HB ist günstig, denn für 25 € kann man 275 Minuten telefonieren.
Hingegen reichen bei HP die 25 € nur für 250 Minuten.
c) Koordinatensystem
Textaufgabe 5
Ein Betrieb kann täglich maximal 1500 Kühlschränke herstellen (Kapazitätsgrenze).
Die fixen Kosten Kf betragen dabei 90000 €.
Die variablen Stückkosten sind konstant und betragen kv = 300 €.
Die Kühlschränke werden zu einem Preis von je 375 € verkauft.
a) Ermittele die Kostenfunktion K(x), die Erlösfunktion E(x) und die Gewinnfunktion G(x) für den Betrieb.
b) Bei welcher Ausbringungsmenge wird die Gewinnschwelle erreicht?
Wie hoch sind an dieser Stelle die Gesamtkosten bzw. der Erlös?
c) Wie groß ist der Gewinn an der Kapazitätsgrenze?
Lösung:
a) Kostenfunktion
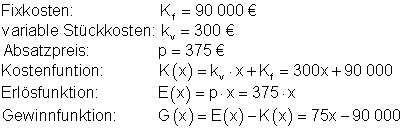
b) Gewinnschwelle
Die Gewinnschwelle ist die Stelle, an der kein Gewinn gemacht wird.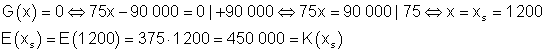
Ab einer täglichen Ausbringungsmenge von 1200 macht der Betrieb also Gewinn.
An der Gewinnschwelle sind die Kosten genau so hoch wie der Erlös (450 000 €).
c) Gewinn an der Kapazitätsgrenze
An der Kapazitätsgrenze beträgt der Gewinn folglich 22 500 €.
Textaufgabe 6
Armin sieht sich die Tarife des Telefonanbieters „Billigsurf“ an.
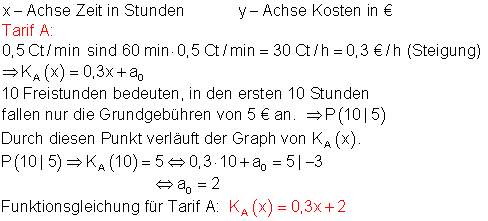
1. Tarif A: Grundgebühr 5 € / Monat die ersten 10 Stunden frei, dann 0,5 Ct. / min.
2. Tarif B: Grundgebühr 10 € / Monat die ersten 20 Stunden frei, dann 0,4 Ct. / min.
3. Tarif C: Flatrate 25 € / Monat.
Durchschnittlich surft Armin zweieinhalb Stunden täglich.
a) Stelle für jeden Tarif die Funktionsgleichung auf.
b) Zeichne die Funktionsgraphen in ein geeignetes Koordinatensystem.
c) Erkläre, was alles aus den Graphen ablesbar ist (Interpretation).
d) Berechne den günstigsten Tarif für Armin.
e) In welchem Punkt herrscht Kostengleichheit für Tarif A und B?
f) Ab welcher Surfzeit sollte Armin die Flatrate wählen?
Lösung:
a) Funktionsgleichung
b) Koordinatensystem
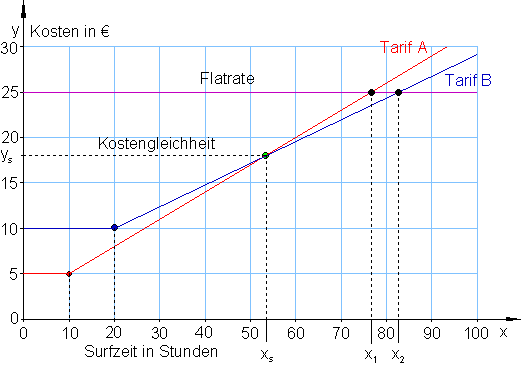
c) Interpretation
Bis etwa 53 Stunden ist Tarif A der günstigste. Zwischen etwa 53 und 82 Stunden ist Tarif B der günstigste. Ab etwa 82 Stunden lohnt sich die Flatrate.
d) Günstigster Tarif für Armin
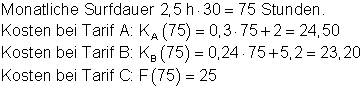
e) Kostengleichheit für Tarif A und B
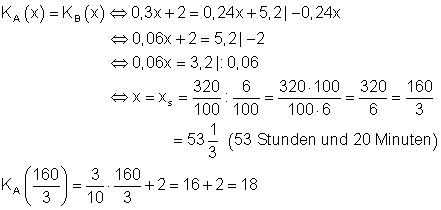
Kostengleichheit herrscht bei einer Surfzeit von 53 h und 20 min. Die für diese Zeit anfallenden Kosten betragen für beide Tarife 18 €.
f) Günstigste Surfzeit
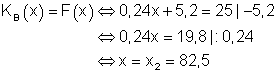
Ab einer Surfdauer von 82,5 Stunden monatlich, sollte man auf die Flatrate umstellen.
Theorie hierzu: Lineare Funktionen aus gegebenen Bedingungen.
Weitere Textaufgaben: Aufgaben lineare Funktionen VII.
Und Aufgaben lineare Funktionen XVIII.
Dazu kannst du auch den Wikipediaartikel über lineare Funktionen lesen.
Hier findest du eine Übersicht über weitere Beiträge zu linearen Funktionen, darin auch Links zu weiteren Aufgaben.
Außerdem findest du hier die Playlist aller Videos zu Funktionen.
