In diesem Beitrag zeige ich anhand vieler Beispiele, wie man den Schnittpunkt zweier Geraden bei Gleichungssystemen mit einer, ohne und unendlich vielen Lösungen berechnet. Anschließend beweise ich, wie die Funktionen von rechtwinklig zueinander verlaufende Geraden zusammenhängen. Zuletzt gehe ich ausführlich auf die Anwendung linearer Gleichungssysteme in der Kostenrechnung ein.
- Schnittpunkt der Geraden bei Gleichungssystem mit einer Lösung
- Schnittpunkt der Geraden bei Gleichungssystem ohne Lösung
- Schnittpunkt der Geraden bei Gleichungssystem mit unendlich vielen Lösungen
- Zusammenfassung
- Rechtwinklig zueinander verlaufende Geraden
- Lineare Gleichungssysteme in der Kostenrechnung
- Mengen- und Geldeinheiten bei der Kostenbetrachtung
Ein lineares Gleichungssysteme mit 2 Gleichungen und 2 Variablen hat bekanntlich entweder eine, keine oder unendlich viele Lösungen. Möglicherweise hängt dies mit der Lage der Geraden zusammen. Aber wie?
Schnittpunkt der Geraden bei einem linearen Gleichungssystem mit einer Lösung:
Dazu schauen wir uns ein praktisches Beispiel an:
Ein Ökokühlschrank (1) kostet 400 € und hat monatliche Energiekosten von 20 €.
Ein Billigkühlschrank (2) kostet 200 €, hat aber monatliche Energiekosten von 40 €.
Wann hat sich der in der Anschaffung teuere Ökokühlschrankbezahlt gemacht (sich amortisiert)?
Die Funktionsgleichungen für die Kostenentwicklung lauten:
Für den Ökokühlschrank:
(1) K1(x) = 20x + 400
Dabei ist x die Zeit in Monaten, K1(x) die Kosten in €.
Für den Billigkühlschrank:
(1) K2(x) = 40x + 200
Dabei ist x die Zeit in Monaten, K2(x) die Kosten in €.
Der in der Anschaffung teuere Ökokühlschrank hat sich dann amortisiert, wenn die Gesamtkosten (Anschaffungskosten und Energiekosten) gleich, bzw. geringer sind als die des Billigkühlschrankes. Mit anderen Worten: Kostengleichheit herrscht, falls K1(x) = K2(x).
K1(x) = K2(x)
\Leftrightarrow 20x + 400 = 40x + 200 \quad | - 400 \\ \Leftrightarrow 20 x = 40x - 200 \quad | - 40x \\ \Leftrightarrow -20x = -200 \quad | : (20) \Leftrightarrow x = 10
Wenn wir dies anschließend in K1(x) einsetzen:
\Rightarrow K_1(10) = 20 \cdot 10 + 400 = 600
Wenn wir dies danach in K2(x) einsetzen:
\Rightarrow K_2(10) = 40 \cdot 10 + 200 = 600
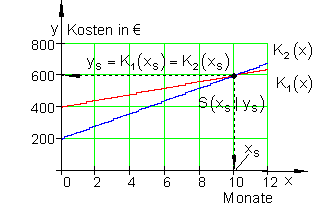
Ergebnis: Das Gleichungssystem K1(x) = 20x + 400 und K2(x) = 40x + 200 haben wir durch das Gleichsetzungverfahren gelöst. Der Wert x = 10 bedeutet, nach 10 Monaten hat sich der Ökokühlschrank amortisiert.
Der Wert y = 600 bedeutet, für beide Kühlschränke sind nach 10 Monaten die gleichen Kosten entstanden ( 600 € ).
Ab jetzt sind die Gesamtkosten für den Ökokühlschrank geringer.
Schnittpunkt der Geraden bei einem linearen Gleichungssystem ohne Lösung
Wenn man den Schnittpunkt zweier Geraden bestimmen will, muss man ein lineares Gleichungssystem mit zwei Variablen lösen.
Beispiel
f(x) = \frac {1}{2}x + 2 \quad g(x) = \frac {1}{2}x -1 \\
f(x) = g(x) \\
\Rightarrow \frac {1}{2}x + 2 = \frac {1}{2}x -1 \\
\Leftrightarrow 2 = - 1
Die Lösung führt dabei auf einen Widerspruch.
Anders gesagt, das Gleichungssystem hat keine Lösung.
Dies können wir auch graphisch darstellen:
f(x) = 0,5x + 2 g(x) = 0,5x – 1
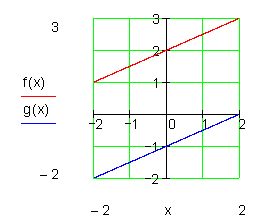
Die Funktionsgleichung g(x) entsteht aus f(x) durch Verschiebung um drei Einheiten nach unten. Mit anderen Worten, der Graph von g(x) ist parallel zu dem von f(x).
Zwei parallele Gerade haben also keinen gemeinsamen Schnittpunkt.
Schnittpunkt der Geraden bei einem linearen Gleichungssystem mit unendlich vielen Lösungen
Beispiel
f(x) = \frac {1}{2}x + 2; \quad g(x) = \frac {1}{2}(x + 2) +1 \\
Schnittpunkt: f(x) = g(x) \\
\Leftrightarrow \frac {1}{2}x + 2 = \frac {1}{2}(x + 2) +1 \\ \Leftrightarrow \frac {1}{2}x + 2 = \frac {1}{2}x + 1 + 1 \\ \Leftrightarrow \frac {1}{2}x + 2 = \frac {1}{2}x + 2
Das ist eine wahre Aussage für alle x ∈ ℝ.
Beide Geraden haben folglich unendlich viele gemeinsame Punkte, sie liegen aufeinander, sind identisch.
Zusammenfassung
Um den Schnittpunkt zweier Geraden zu bestimmen, muss man deren Funktionsgleichungen lösen. Die beiden bilden ein lineares Gleichungssystem mit zwei Variablen. Folglich muss man es mit dem Gleichsetzungsverfahren lösen.
Merke:
Wenn f(x) = g(x) genau eine Lösung hat, dann schneiden sich die Graphen von f und g in einem Punkt. Die Geraden haben unterschiedliche Steigungen.
Hat f(x) = g(x) keine Lösung, dann haben beide Geraden keinen gemeinsamen Punkt. Sie verlaufen parallel zueinander.
Wenn f(x) = g(x) unendlich viele Lösungen hat, dann sind beide Geraden identisch.
Genau eine Lösung
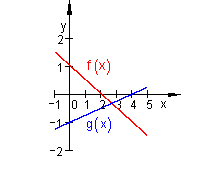
Keine Lösung
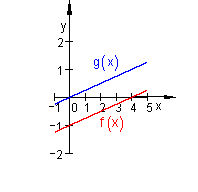
Unendlich viele Lösungen

Rechtwinklig zueinander verlaufende Geraden
Ermittelt man die Steigung von zwei sich rechtwinklig schneidenden Geraden, dann gibt es zwischen den Steigungen beider Geraden wahrscheinlich einen Zusammenhang.
Vorübung:
Zeichne den Graphen der Funktion f(x) = \frac{3}{2}x in ein Koordinatensystem!
Zeichne danach zu diesem Graphen mit dem Geodreieck eine senkrechte Gerade durch den Koordinatenursprung und lesen Sie deren Steigung ab!
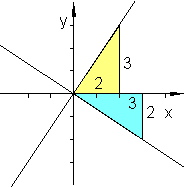
Die Steigung der Gerade g: a_g = \frac{3}{2}
Deshalb vermuten wir, dass die Steigung der Gerade h: a_h = - \frac{3}{2}x .
Denn ah stellt den negativen Kehrwert von ag dar. Mathemathisch ausgedrückt: ein negativ-reziprokes Steigungverhältnis. Das bedeutet ah = - \frac{1}{a_g} \quad bzw. \quad a_g \cdot a_h = -1 \quad oder \quad a_g = - \frac{1}{a_h} .
Orthogonal:
Für die Steigung zweier senkrecht aufeinander stehender Geraden g und h gilt:
a_g \cdot a_h = -1 \quad bzw. \quad a_h = - \frac{1}{a_g} \quad oder \quad a_g = - \frac{1}{a_h} .
Die Geraden sind zueinander orthogonal.
Beweis: Die Steigungen von g und h lassen sich ablesen zu:
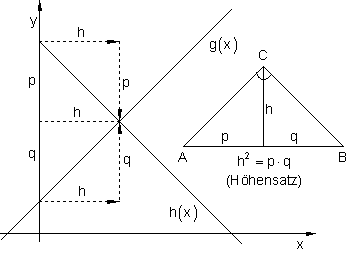
a_g = \frac{q}{h} \quad und \quad a_h = -\frac{p}{h} \\
a_g \cdot a_h = \frac{q}{h} \cdot (-\frac{p}{h}) = -\frac{q \cdot p}{h^2} \quad (1).
Nach dem Höhensatz ist h^2 = p \cdot q .
Wenn wir dies in (1) einsetzen, erhalten wir:
a_g \cdot a_h = -\frac{q \cdot p}{h^2} = - \frac{h^2}{h^2} = -1 \\
\Rightarrow \color{red}{a_g \cdot a_h = -1} .
Beispiel:
Gegeben ist der Schnittpunkt S( 2 | 3 ) zweier rechtwinklig zueinander verlaufender Geraden g und h, wobei die Steigung von g a_g = \frac{1}{2} .
Gesucht:
Die Funktionsgleichung g(x) der Geraden g.
Ferner Funktionsgleichung h(x) der Geraden h.
Außerdem die Graphen von g und h für
D = \{x | -5 \le x \le 4 \} _ℝ
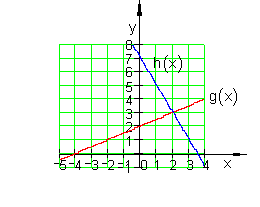
a_g = \frac{1}{2} \quad wegen \quad g(x) \perp h(x) \quad folgt \quad a_h = -2 \\ g(x) = \frac{1}{2} x + a_g \quad und \quad h(x) = -2x + a_h \\ S(2 | 3) \Rightarrow g(2) = 3 \Leftrightarrow \frac{1}{2} \cdot 2 + a_g = 3 \Leftrightarrow a_g = 2 \\ S(2 | 3) \Rightarrow h(2) = 3 \Leftrightarrow 2 \cdot 2 + a_h = 3 \Leftrightarrow a_h = 7 \\ \Rightarrow g(x) = \frac{1}{2} x +2 \quad und \quad h(x) = -2x +7 .
Schnittpunkt zweier Geraden
Interaktiv: Geben Sie Dezimalzahlen oder Brüche für a ein, klicken Sie auf ‚Berechnen‘, dann werden die Funktionsgleichungen und die Schnittpunkte berechnet. Klicken Sie danach auf ‚Zeichne g1‘ und ‚Zeichen gn2‘ und die Graphen werden gezeichnet.
Lineare Gleichungssysteme in der Kostenrechnung
In der betrieblichen Kostenrechnung wird der Schnittpunkt zweier Geraden oft genutzt, um bestimmte Grenzwerte zu berechnen. So ist es für einen Unternehmer wichtig, diejenige Produktionsmenge x einer Ware zu kennen, bei der die ihm bei der Produktion entstandenen Kosten K durch die Erlöse E aus dem Verkauf (Absatz) gedeckt sind. Anders ausgedrückt, er interessiert sich dafür, ab welcher produzierten Menge x er Gewinn G macht.
Definition:
Für die Kostenfunktion K(x) bei konstanten Stück- und Fixkosten gilt:
Gesamtkosten K(x) = Stückkosten k \cdot Produktionsmenge x + fixe Kosten Kf.
K(x) = k \cdot x + Kf falls Stückkosten und Fixkosten konstant sind.
Merke:
Gesamtkosten, beschrieben durch die ertragliche Kostenfunktion K(x) sind die in einem Betrieb bei der Produktion von x Mengeneinheiten (ME) eines Produktes entstehenden Kosten.
Stückkosten k sind die Gesamtkosten pro Stück (auch variable Stückkosten genannt).
Fixe Kosten Kf sind die Kosten, die auch dann entstehen, wenn nichts produziert wird. (Zinsen, Mieten, Versicherungen, Gehälter usw.)
Definition:
Für die Erlösfunktion E(x) bei konstantem Preis gilt:
Erlös E(x) = Preis p \cdot Menge x, also E(x) = p \cdot x.
Merke:
die zu dem Preis p verkaufte Menge nennt man auch Ausbringungsmenge.
Definition:
Für die Gewinnfunktion G(x) gilt:
Gewinn G(x) = E(x) – K(x).
Merke:
Wenn das Ergebnis von G(x) negativ ist, macht der Betrieb Verlust. Falls G(x) positiv ist, dann macht er Gewinn.
Wenn G(x) = 0 ist, sind die Kosten K(x) genauso hoch wie der Erlös E(x).
Dieser Punkt wird Gewinnschwelle genannt.
Beispiel:
Ein Betrieb produziert „Handys“ zu 20 € pro Stück.
Die fixen Betriebskosten belaufen sich dabei auf 60000 € pro Tag.
Der Verkaufspreis pro „Handy“ beträgt 40 €.
Maximal kann der Betrieb täglich 4000 „Handys“ herstellen (Kapazitätsgrenze).
a) Ab welcher Ausbringungsmenge macht der Betrieb Gewinn?
b) Bei welcher Ausbringungsmenge erzielt der Betrieb den maximalen Gewinn?
c) Stelle den Sachverhalt graphisch in einem geeigneten Koordinatensystem dar!
Lösung:
a) Als erstes stellen wir die Funktionsgleichungen auf:
Kostenfunktion: K(x) = 20x + 60000
Erlösfunktion: E(x) = 40x
Gewinnfunktion: G(x) = E(x) - K(x) \\
= 40x - 20x - 60000\\
= 20x - 60000
Als nächstes folgt der Ansatz: G(x) > 0
\Leftrightarrow 20x - 60000 < 0 | + 60000\\
\Leftrightarrow 20x > 60000 | : 20 \Leftrightarrow x > 3000
.
Daraus folgt: Ab einer Ausbringungsmenge von x = 3000 Handys pro Tag macht der Betrieb Gewinn. Bei x = 3000 sind die Kosten K(x) genauso hoch wie der Erlös E(x).
K(3000) = 20 \cdot 3000 + 60000 = 120000 \\
E(3000) = 40 \cdot 3000 = 120000
b) Gewinnermittlung bei maximaler Ausbringungsmenge xMax = 4000
G(4000) = 20 \cdot 4000 - 60000 = 20000 .
c)
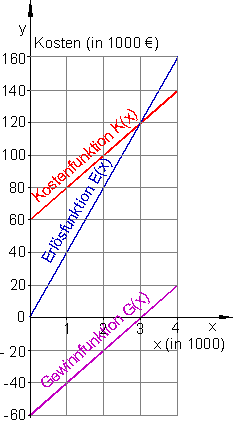
Folglich ist der Gewinn bei einer Ausbringungsmenge von 4000 „Handys“ pro Tag maximal, er beträgt dann 20000 €.
Die Gewinnschwelle kann man statt über die Gewinnfunktion auch über den Schnittpunkt des Graphen der Kostenfunktion mit dem Graphen der Erlösfunktion ermitteln.
Die x-Koordinate des Schnittpunktes ist dann die Gewinnschwelle, die y-Koordinate gibt die Kosten an dieser Stelle an.
Mengen- und Geldeinheiten bei der Kostenbetrachtung
Die in einem Betrieb produzierte Menge eines Produktes beläuft sich oft auf große Stückzahlen, z.B 1000 000 CD- Rohlinge pro Tag. Auch Kosten für Produktionsprozesse fallen häufig in Millionenhöhe an.
Solch große Zahlen sind bei Rechnungen nicht immer leicht zu handhaben. Deshalb führt man für die produzierte Stückzahl Mengeneinheiten und für Kosten Geldeinheiten ein.
Dabei kann man z. B. 1000 000 CD- Rohlinge zu 10 Mengeneinheiten (10 ME) zusammenfassen, wobei eine Mengeneinheit für 100 000 Stück steht.
Ebenso fasst man Kosten zu Geldeinheiten zusammen, z. B. können 9000 000 € zu 9 Geldeinheiten (9 GE) zu je 1000 000 € zusammengefasst werden.
Außerdem ist man bei der Kostenbetrachtung an keine bestimmte Währung gebunden. Man betrachtet lediglich Geldeinheiten.
Beispiel:
Die Kostenfunktion für die Herstellung eines bestimmten Produktes sei K(x) = 0,3x + 4 und die Erlösfunktion E(x) = 1,1x.
Wie hoch sind die Gesamtkosten an der Gewinnschwelle?
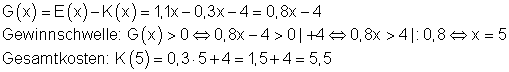
Die Gewinnschwelle liegt bei 5 ME, an dieser betragen die Kosten 5,5 GE.
Hier findest du Aufgaben dazu: Aufgaben Lineare Funktionen IV Schnittpunkte mehrerer Geraden.
Und Aufgaben Lineare Funktionen Aufgaben V Schnittpunkte mehrerer Geraden.
Hier findest du eine Übersicht über weitere Beiträge zu linearen Funktionen, darin auch Links zu weiteren Aufgaben.


