Im letzten Beitrag habe ich eine Einführung in die mathematischen Funktionen gegeben. Hier demonstriere ich zuerst die Begriffe Zuordnungsvorschrift und inverse Funktion anhand eines anschaulichen Beispiels. Danach zeige ich die Besonderheiten bei der Umkehrfunktion der linearen, quadratischen und e-Funktion.
Umkehrfunktionen
Die Zuordnungsvorschrift f wird ausgedrückt durch die Funktionsgleichung.
Wenn die Funktion eineindeutig, existiert auch eine eindeutige Zuordnung von f-1. Mit anderen Worten: Es gibt eine Umkehrfunktion oder inverse Funktion.
Beispiel:
Wenn wir in die Funktion f(x) = 2x für x den Wert 2 eingeben, ergibt sich für f(x) = 4 .
Die Umkehrfunktion dazu lautet f^{-1} = \frac{1}{2} . Wenn wir hier für x den Wert 4 eingeben, ergibt sich für f^{-1} = 2 . Also stimmt dies.
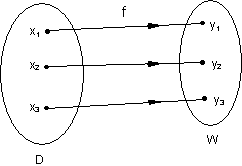
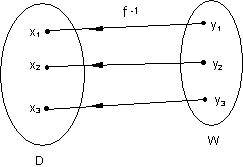
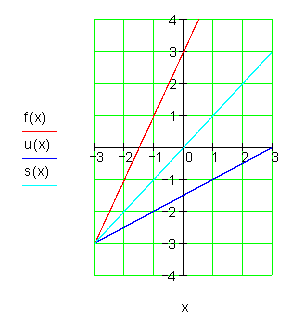
Die Umkehrfunktion der linearen Funktion
Beispiel:
Gegeben ist die Funktion
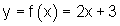
Folglich hat die Funktion f die Steigung m = 2. Das heißt, sie schneidet mit ihrem Graph die Abszissenachse im Punkt Px ( -1,5 | 0 ) und die Ordinatenachse im Punkt Py ( 0 | 3 ). Ihr Graph ist eine Gerade.
Nun vertauscht man die Variablen der Funktionsgleichung miteinander, z. B x und y. Danach formt man nach y äquivalent um. Dann erhält man die Umkehrfunktion.
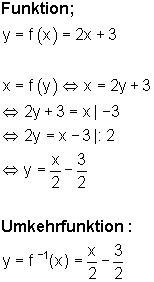
Dazu kannst du dir dieses 📽️Video Umkehrfunktion einer linearen Funktion bilden ansehen.
Der Graph der Umkehrfunktion ist die Spiegelung des Funktionsgraphen an der 450 -Achse.
Allgemein gilt:
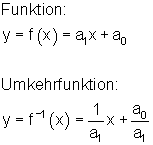
Der Einfachheit halber nennen wir die Umkehrfunktion u(x).
Dazu kannst du dir dieses 📽️Video Umkehrfunktion einer linearen Funktion zeichnen ansehen.
Die Umkehrfunktion der quadratischen Funktion
Die Vorgehensweise ist die gleiche wie oben bei der linearen Funktion gezeigt.

Bei der Bildung der Umkehrfunktionen wird die Definitionsmenge eingeschränkt, damit eindeutige Zuordnungen entstehen.
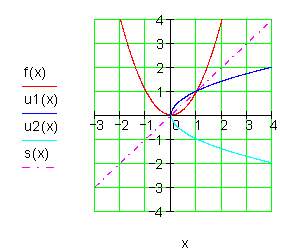
Dazu kannst du dir dieses 📽️Video Umkehrfunktion einer quadratischen Funktion bilden ansehen.
Die Umkehrfunktion der e-Funktion

Bei der Bildung der Umkehrfunktionen wird ebenfalls die Definitionsmenge eingeschränkt, denn der Logarithmus ist nur für positive x- Werte definiert.
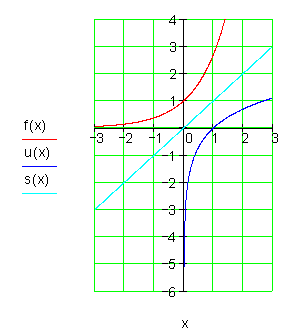
Zu diesem Thema gibt es ausnahmsweise keine Aufgaben.
Hier findest du eine Übersicht über weitere Beiträge zu linearen Funktionen, darin auch Links zu weiteren Aufgaben.
Im nächsten Beitrag Einführung lineare Funktionen wird das Thema vertieft.


