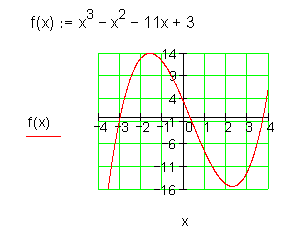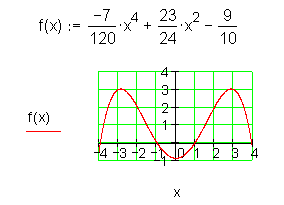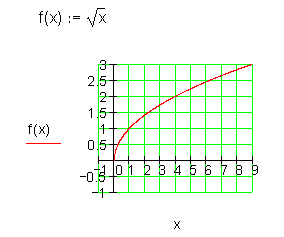Funktionen in der Mathematik einfach erklärt

Im letzen Beitrag Relationen und Funktionen haben wir anhand eines Beispiels gesehen, dass eine Relation eine Paarmenge ist, bei der die Elemente aufgrund einer Zuordnungsvorschrift gebildet werden. Außerdem verstehen wir in der Mathematik unter einer Funktion eine zumindest eindeutige Relation. In diesem Beitrag stelle ich zuerst ein paar Beispiele und Übungen für Funktionen vor. Danach zeige ich, wie man eine Wertetabelle für eine Funktionen erstellt. Dazu ich stelle ein interaktiven JavaScript dazu zur Verfügung. Anschließend erkläre ich, welche Arten von Funktionen es gibt und die mathematischen Schreibweise dazu. Danach stelle ich Beispiele für mathematische Funktionen und Funktionsgleichungen anhand ihrer Graphen vor. Schließlich zeige ich die Definition der Definitionsmenge D und der Wertemenge W. Zuletzt gebe ich Tipps zur Vorgehensweise bei Aufgaben zu Funktionen.

Bei der mathematischen Betrachtung natürlicher, technischer oder auch alltäglicher Vorgänge hängt der Wert einer Größe oft vom Wert einer anderen Größe ab. Zum Beispiel hängt der Benzinverbrauch eines Autos von der Geschwindigkeit ab.

Beispiele für Funktionen:

Der Preis einer Ware hängt von der verkauften Menge ab.
Die Note einer Mathematikarbeit hängt von der erreichten Punktzahl ab.

Übung 1 für Funktionen:

Finde weitere Beispiele für solche Abhängigkeiten!
Mögliche Lösungen dazu findest du unten.

Mit anderen Worten: jeweils zwei Größen werden einander zugeordnet.

Menge  Preis Die verkaufte Menge beeinflusst den Preis.
Punktzahl Note Die in einer Klausur erreichte Punktzahl beeinflusst die Note.

Übung 2 für Funktionen:

Formuliere die Zusammenhänge für deine Beispiele!

Definition abhängige und unabhängige Variable:

Die einander zugeordneten Größen nennt man Variablen.
Dabei ist zu überlegen, welche Abhängigkeit zwischen den Variablen besteht.

Die Note einer Mathematikarbeit hängt aus Sicht des Lehrers von der erreichten Punktzahl ab. Jedoch hängt die Punktzahl nicht von der Note ab.
Man bezeichnet daher die Note auch als abhängige Variable und die Punktzahl als unabhängige Variable.
Mit anderen Worten, es besteht ein funktionaler Zusammenhang zwischen der Punktzahl und der Note.

Es gibt es mehrere Möglichkeiten, den funktionalen Zusammenhang zweier Variablen zu beschreiben bzw. darzustellen.
Dazu nur das Beispiel des Bremswegs eines Autos.

Wie erstellt man eine Wertetabelle:

Für verschiedene Geschwindigkeiten wird der Bremsweg gemessen und in eine Wertetabelle eingetragen.

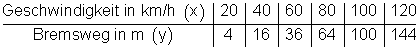
Wertetabelle einer Funktion erstellen
Interaktiv: Mit diesem JavaScript kannst du eine Wertetabelle für ganzrationale Funktionen bis 4. Grades erstellen.

Wenn man die Tabellenwerte in ein Koordinatensystem einträgt und die Punkte miteinander verbindet, dann erhält man den Graphen der Funktion. Dieser beschreibt den Zusammenhang zwischen Geschwindigkeit und Bremsweg. Danach findet man auf der waagerechten Achse die Werte der unabhängigen Variablen x. Auf der senkrechten Achse findet man entsprechend die Werte der abhängigen Variablen y = f(x). Die waagerechten Achse wird auch Abszisse genannt, die senkrechte Ordinate.

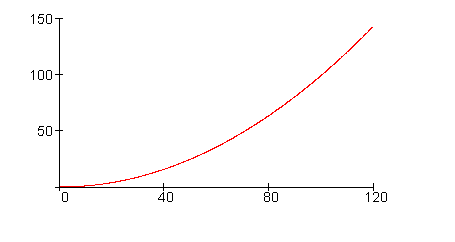
Übung 3:

Trage entsprechend der Wertetabelle die Punkte in ein geeignetes Koordinatensystem und verbinde diese zu einem Graphen.
Bestimme durch Ablesen den Bremsweg für die Geschwindigkeiten 30 ; 50 ; 70 ; 90 und 110 km/h.
Wenn die Polizei einen Bremsweg von 90 m misst, wie schnell war dann das Fahrzeug?

Oft ist es auch möglich den funktionalen Zusammenhang durch eine Funktionsgleichung darzustellen.
Für den Bremsweg gilt: y = f(x) = 0,01 x².
Dabei steht y = f(x) für den Bremsweg und besagt, dass die y-Koordinate im Koordinatensystem von der Variablen x abhängt. Mit anderen Worten, die y-Koordinate ist eine Funktion der unabhängigen Variablen x.
f(x) = 0,01 x² ist die Funktionsgleichung, welche die Vorschrift angibt, wie die Werte für die abhängige Variable f(x) zu bilden sind.
Anders ausgedrückt f(x) = 0,01 x² ist die Funktionsvorschrift.

Übung 4:

Berechne die abgelesenen Werte, wenn die Funktionsgleichung f(x) = 0,01 x² lautet.

Nachdem bisher Erarbeiteten lässt sich sagen:

Definition der Funktion in der Mathematik:

Bei einer Funktion wird jedem Wert der unabhängigen Variablen x genau ein Funktionswert f(x) zugeordnet. Anders ausgedrückt handelt es sich bei einer Funktion um eine eindeutige Zuordnung, bei der einer unabhängigen Variablen x aus der Definitionsmenge D genau ein Funktionswert f(x) zugeordnet wird. Dabei wird der funktionale Zusammenhang durch eine Funktionsgleichung beschrieben. Durch Einsetzen von x-Werten in die Funktionsgleichung erhält man Funktionswerte, die zusammen mit den x- Werten in einer Wertetabelle dargestellt werden können. Jedes Wertepaar der Tabelle entspricht dabei genau einem Punkt im kartesischen Koordinatensystem. In vielen Fällen lassen sich die so entstandenen Punkte zu einem Graphen verbinden. Die Menge aller x- Werte, die in die Funktionsgleichung eingesetzt werden dürfen, heißt Definitionsmenge. Die Menge aller Funktionswerte, die dabei entstehen, gehören zur Wertemenge W der Funktion.

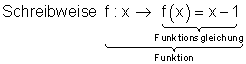
Wenn ich von einer Funktion spreche, dann gebe ich zur Beschreibung dieser lediglich die Funktionsgleichung an. Also nur noch f(x) = …..

Der Name der Funktion ist f.
Die Schreibweise x → f(x) verdeutlicht dabei, dass zu jedem x- Wert ein bestimmter Funktionswert gehört.
Die Funktionsgleichung f (x) = x – 1 gibt die Rechenvorschrift an, wie die Funktionswerte gebildet werden.

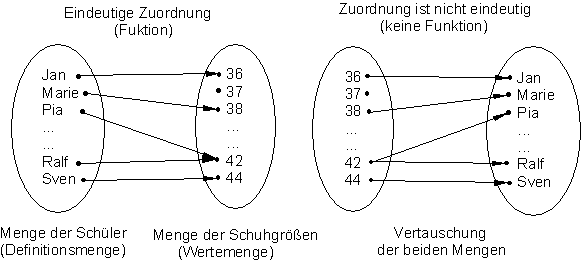
Z. B. hat jeder Schüler eine bestimmte Schuhgröße. Dabei ist es unerheblich, dass mehrere Schüler die gleiche Schuhgröße haben.
Die Eindeutigkeit bezieht sich dabei von Schüler → Schuhgröße.
Ausgedrückt durch Variablen heißt das, der Name des Schülers bildet die unabhängige Variable, die ihm zugeordnete Schuhgröße die abhängige Variable.
Umgekehrt ist die Zuordnung der Schuhgröße zu Schülern nicht eindeutig, denn mehrere Schüler können z. B. die Schuhgröße 42 haben.
Eine Funktion dieser Art hat keine Funktionsgleichung, sie kann aber als Mengenbild dargestellt werden.

---

Beispiele mathematischer Funktionen und Funktionsgleichungen

 
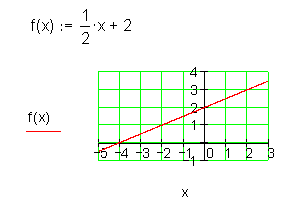
Lineare Funktion (Gerade)

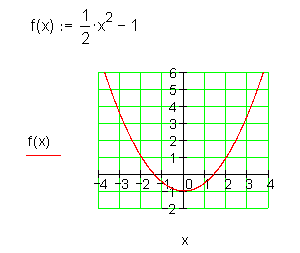
Quadratische Funktion (Parabel)

  

Ganzrationale Funktion 3. Grades

Ganzrationale Funktion 4. Grades

  

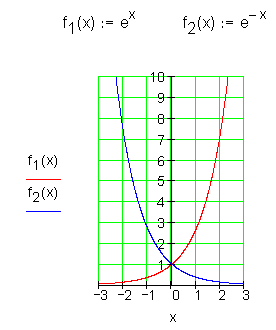
Exponentialfunktionen

Wurzelfunktion

  
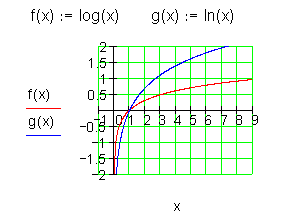
Logarithmusfunktionen

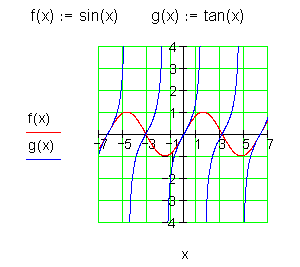
Trigonometrische Funktionen

  
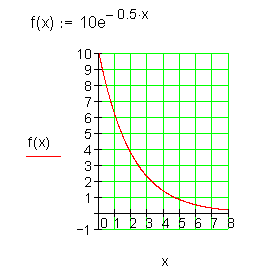
exponentielles abklingen

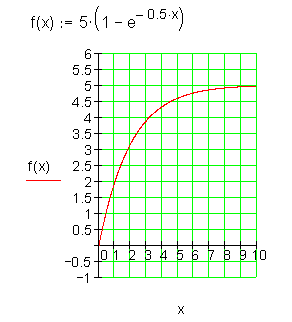
exponentielle Sättigungskurve

  
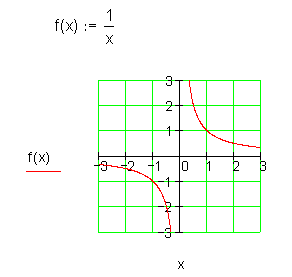
Hyperbel punktsymmetrisch

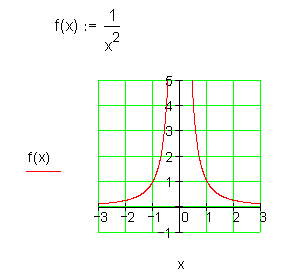
Hyperbel achsensymmetrisch

---

Definition der Definitionsmenge D

Die Definitionsmenge einer Funktion ist die Menge aller unabhängigen Variablen, für die die Funktion definiert ist.
Mit anderen Worten: in der Regel ist dies die Menge aller Werte, die für x eingesetzt werden darf. Das ist meist die Menge der reellen Zahlen. Die wird mit diesem Zeichen dargestellt: ℝ. Einschränkungen gibt es hauptsächlich in drei Fällen:

1. Brüche: der Nennen darf nicht Null werden, denn durch Null darf nicht dividiert werden
2. Wurzeln: man kann nur die Wurzel aus Zahlen ziehen, die größer oder gleich Null sind
3. Logarithmen: man kann nur den Logarithmus von positiven Zahlen berechnen.

Ein paar Beispiele dazu kannst du dir in diesem 📽️ Video Funktionen Definitionsmenge ansehen.

Definition der Wertemenge W

Die Wertemenge einer Funktion ist die Menge aller Funktionswerte, die aus den Elementen von D entstehen.
Anders ausgedrückt: das ist meist die Menge aller Werte, die sich für y ergeben, wenn man die Funktion berechnet.

Beispiel 1: 

Beispiel 2:
Achtung! Dabei darf nicht durch Null dividiert werden!

Beispiel 3:
Die Funktion kann jeden beliebigen Wert annehmen.

Beispiel 4:
Als Funktionswerte treten nur positive Werte auf.

---

Mathematische Schreibweise bei Funktionsgleichungen und deren Bedeutung

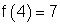
Für den Wert der unabhängigen Variablen x = 4 ist der Funktionswert 7.
Das Wertepaar ( 4 | 7 ) bildet dabei die Koordinaten des Punktes P ( 4 | 7 ) im Koordinatensystem.

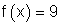
Gesucht wird der x-Wert, zu dem der Funktionswert 9 gehört.

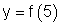
y ist der Funktionswert für x = 5.

---

Zusammenfassung

Eine eindeutige Zuordnung, bei der einer unabhängigen Variablen x aus der Definitionsmenge D genau ein Funktionswert f(x) zugeordnet wird, heißt Funktion.

Der funktionale Zusammenhang wird durch eine Funktionsgleichung (z.B. f(x) = 2x + 1 ) beschrieben.
Durch Einsetzen von x-Werten in die Funktionsgleichung erhält man Funktionswerte. Diese kann man anschließend zusammen mit den x-Werten in einer Wertetabelle darstellen.

Jedes Wertepaar der Tabelle entspricht dabei genau einem Punkt im kartesischen Koordinatensystem.

In vielen Fällen lassen sich die so entstandenen Punkte zu einem Graphen verbinden.
Die Menge aller x-Werte, die in die Funktionsgleichung eingesetzt werden dürfen, heißt Definitionsmenge.
Die Menge aller Funktionswerte, die dabei entstehen, gehören zur Wertemenge W der Funktion.

---

Lösungen der Übungen

Übung 1: 

Finde weitere Beispiele für solche Abhängigkeiten.
Lösung: Du kannst z. B. diese finden:
Die Leistung eines Verbrennungsmotors hängt von der Drehzahl ab.
Die Fläche eines Kreises hängt von seinem Radius ab.
Die Stromrechnung hängt bei konstantem kWh- Preis von der Energiemenge ab.

Übung 2:

Formuliere die Zusammenhänge für Ihre Beispiele!
Lösung:

Drehzahl  Leistung Die Drehzahl eines Verbrennungsmotors beeinflusst die Motorleistung.
Radius  Fläche Der Radius eines Kreises beeinflusst seine Fläche.
Energiemenge  Stromrechnung Die genutzte Energiemenge beeinflusst die Stromrechnung.

Übung 3:

Trage entsprechend der Wertetabelle die Punkte in ein geeignetes Koordinatensystem und verbinde diese zu einem Graphen.
Bestimme durch Ablesen den Bremsweg für die Geschwindigkeiten 30 ; 50 ; 70 ; 90 und 110 km/h.
Wenn die Polizei einen Bremsweg von 90 m misst, wie schnell war dann das Fahrzeug?
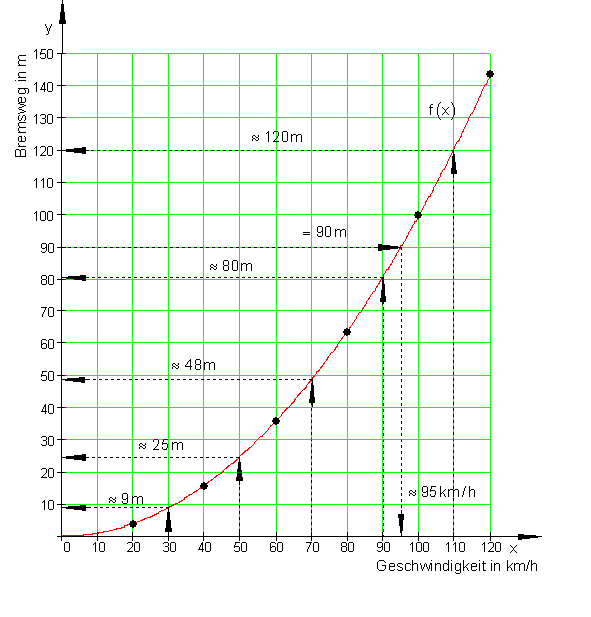
Lösung: Für die Geschwindigkeit von
30 km/h beträgt der Bremsweg etwa 9 m.
50 km/h beträgt der Bremsweg etwa 25 m.
70 km/h beträgt der Bremsweg etwa 48 m.
90 km/h beträgt der Bremsweg etwa 80 m.

Für die Geschwindigkeit von 110 km/h beträgt der Bremsweg etwa 120 m.
Also fuhr das Fahrzeug bei einem gemessenen Bremsweg von 90 m  mit einer Geschwindigkeit von etwa 95 km/h.

Tipps zur Vorgehensweise bei Aufgaben zu Funktionen:

• Die x-Achse (Abszisse) des Koordinatensystems repräsentiert die Menge der unabhängigen Variablen, die y-Achse (Ordinate) die der abhängigen Variablen.
• Bevor Wertepaare in ein Koordinatensystem als Punkte eingetragen werden, muss man überlegen, welche die unabhängige und welche die abhängige Variable ist.
• Außerdem ist es wichtig einen geeigneten Maßstab für die Skalierung der Achsen zu finden.
• Dazu schaut man sich die größten und die kleinsten Werte der Tabelle an und entscheidet in wie viel Teile die beiden Achsen einzuteilen sind.
• Wenn man dann entsprechend der Wertetabelle alle Punkte in das Koordinatensystem eingetragen hat, verbindet man diese zu einem Graphen.
• Danach kann man aus dem Graphen auch für solche x-Werte, die nicht in der Wertetabelle vorkommen, die entsprechenden Funktionswerte in etwa ablesen.
• Außerdem kann man für einen bestimmten Funktionswert den zugehörigen x-Wert ablesen. Die Genauigkeit der Ergebnisse hängt davon ab, wie genau der Graph gezeichnet wurde.

Übung 4:

Berechne die abgelesenen Werte, wenn die Funktionsgleichung f (x) = 0,01 x² lautet.
Lösung:
Die Funktionswerte werden berechnet, indem man die entsprechenden x- Werte in die Funktionsgleichung einsetzt.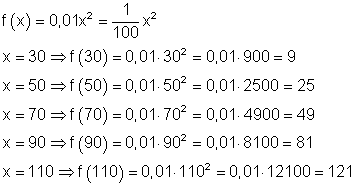

Bei einer Geschwindigkeit von
30 km/h beträgt der Bremsweg 9 m.
50 km/h beträgt der Bremsweg 25 m.
70 km/h beträgt der Bremsweg 49 m.
90 km/h beträgt der Bremsweg 81 m.
110 km/h beträgt der Bremsweg 121 m.

Gemessen wurde ein Bremsweg von 90 m, gesucht ist die Geschwindigkeit.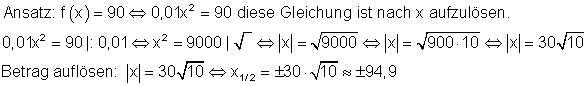

Nur der positive Wert ist in Bezug der Aufgabenstellung sinnvoll, da wir nur positive Geschwindigkeiten betrachten. Bei einem gemessenen Bremsweg von 90 m betrug die Geschwindigkeit etwa 94,9 km/h.

Bemerkung:
Erst die Rechnung liefert genaue Werte. Dennoch ist es sinnvoll, die berechneten Werte durch Ablesen auf dem Graphen zu kontrollieren.

Hier findest du Aufgaben zu Funktionen II

und hier Aufgaben zu Fnktionen VII

Hier findest du eine Übersicht über weitere Beiträge zu Funktionen. Darin auch Links zu weiteren Aufgaben.

Im nächsten Beitrag Funktion und Umkehrfunktion wird das Thema vertieft.