Bisher haben wir uns mit Gleichungen in der Form y = 3x beschäftigt. In diesem Beitrag gebe ich anhand eines Beispiels eine Einführung in mathematische Relationen und Funktionen. Zuerst definiere ich die beiden Begriffe und Produktmenge. Danach zeige ich, wie man Relationen im kartesischen Koordinatensystem darstellen kann. Anschließend erkläre ich anhand eines anschaulichen Beispiels die Begriffe eindeutige Relation, eineindeutige Relation und den Funktionsbegriff. Schließlich zeige ich die Darstellungsarten von Funktionen: Mengenschreibweise und Zuordnungsschreibweise.
Beispiel Relation:
Während eines Fluges bietet eine Stewardess Süßigkeiten an.
Der Vater greift zu Pfefferminz und Fruchtbonbon, die Mutter jedoch Fruchtbonbons, das Kind Kaugummi und Fruchtbonbon.
Im Pfeildiagramm kann man zeigen, wer was isst. Dabei können wir die Definitionsmenge und Wertemenge einführen:
D = Definitionsmenge
W = Wertemenge
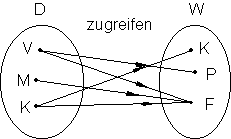
Dadurch entstehen geordnete Paare, die man zu einer Relation R zusammenfassen kann.
![]()
Definition der mathematischen Relation:
Eine Paarmenge, bei der die Elemente aufgrund einer Zuordnungsvorschrift gebildet werden, heißt Relation.
Wenn alle drei von jeder Süßigkeiten etwas nehmen, erhält man eine besondere Relation, die Produktmenge D x W.
![]()
Die Produktmenge D x W umfasst also alle Zuordnungsmöglichkeiten (jeder nimmt von jedem). Damit ist auch jede Teilmenge der Produktmenge eine Relation.
Definition der Produktmenge:
![]()
![]()
Darstellung von Relationen im kartesischen Koordinatensystem
Eine Zahl kann man als Punkt auf der Zahlengeraden darstellen. Bei einem Zahlenpaar benutzt man jedoch dafür die Zahlenebene. Zwei Zahlengeraden kreuzen sich dabei senkrecht und bilden ein Gitternetz.
Die waagerechte Zahlengerade heißt dabei x -Achse oder Abszissenachse, die senkrechte y-Achse oder Ordinatenachse.
Der Schnittpunkt der x – und der y-Achse heißt 0-Punkt oder Ursprung. Die Einteilung der Zahlenabschnitte in Einheiten kann jedoch auf beiden Achsen verschieden sein.
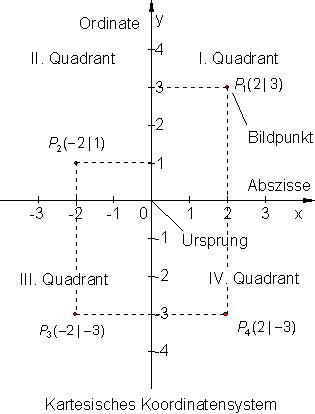
Die beiden Komponenten eines Zahlenpaares oder allgemein eines Variabelenpaares (x | y) nennt man Koordinaten.
Dabei steht die Abszisse (x-Koordinate) an erster Stelle, die Ordinate (y-Koordinate) an zweiter Stelle des Variabelenpaares. Zu jedem Zahlenpaar (x | y) gehört dadurch ein Bildpunkt P (x | y).
Das untenstehende Gitternetz heißt nach dem französischen Mathematiker und Philosophen Rene Descartes rechtwinkliges oder Kartesisches Koordinatensystem. Die Achsen teilen das Koordinatensystem in 4 Felder (Quadranten) I., II., III., und IV. An dem Vorzeichen der Koordinaten erkennt man, in welchem Quadranten der betreffende Punkt liegt. P1 (2 | 3) liegt im I. Quadranten
P2 (-2 | 1) liegt im II. Quadranten
P3 (-2 | -3) liegt im III. Quadranten
P4 (2 | -3) liegt im IV. Quadranten
Beispiel Relation:


d) Der Graph der Relation besteht nur aus Punkten.
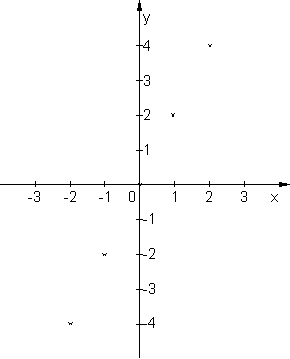
e) Der Graph der Relation in IR x IR besteht dagegen aus einer durchgezogenen Linie.
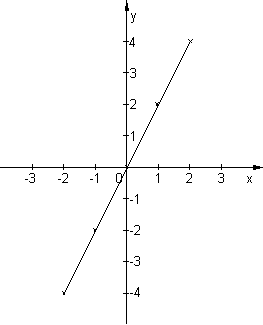
Der Funktionsbegriff
Später bietet die Stewardess Zeitschriften an: eine Frankfurter Allgemeine Zeitung, ein Modejournal und ein Comicheft.
Der Vater nimmt die FAZ, die Mutter jedoch das Modejournal, das Kind das Comicheft.
Dadurch entsteht eine eindeutige Relation.
![]()
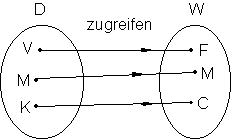
Definition eindeutige Relation:
Eine Relation heißt eindeutig, wenn jedem Element der Definitionsmenge genau ein Element der Wertemenge zugeordnet ist.
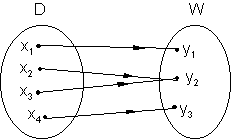
Definition eineindeutige Relation:
Eine Relation heißt eineindeutig, wenn die Zuordnung auch umkehrbar eindeutig ist. D.h. jedem Element aus D ist genau ein Element aus W und jedem Element aus W genau ein Element aus D zugeordnet.
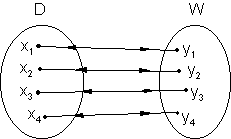
Definition der Funktion in der Mathematik:
Eine zumindest eindeutige Relation R heißt Funktion f.
![]()
Darstellungsarten von Funktionen
![]()
Die Funktion f ist die Menge aller geordneten Paare (x | y), für die die Funktionsgleichung y = f(x) gilt in der Grundmenge D x W.
![]()
Die Funktion f ist definiert als die Zuordnung: x wird zugeordnet einem f(x) mit der Funktionsgleichung f(x) = y in der Grundmenge D x W.
Im folgenden bevorzuge ich die Mengenschreibweise.
Beispiel Funktion:

Graph
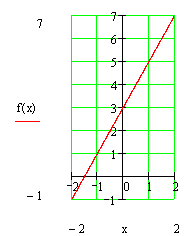
Hier findest du Aufgaben zu Funktionen II.
Außerdem hier Aufgaben zu Fnktionen VII.
Hier findest du eine Übersicht über weitere Beiträge zu Funktionen. Darin auch Links zu weiteren Aufgaben.
Im nächsten Beitrag Funktionen in der Mathematik wird das Thema vertieft.