Hier findest du Aufgaben zum Schnittpunkt zweier Geraden. Zuerst sind die beiden Funktionsgleichungen bekannt. Danach eine Funktionsgleichung und ein Punkt der anderen Geraden. Dabei liegen die Geraden senkrecht zueinander.
1. Teil: Funktionsgleichungen bekannt
Gegeben sind die Funktionsgleichungen zweier Geraden g1(x) und g2(x).
Berechne den Schnittpunkt beider Geraden. Zeichne danach die Geraden in ein Koordinatensystem.
Tipps zum Vorgehen anhand eines Beispiels beim 1. Teil:
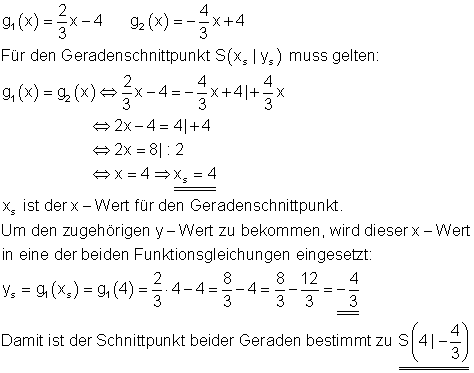
Vorgehensweise:
Der Schnittpunkt liegt auf beiden Geraden. Das heißt, die Schnittpunktkoordinaten gelten für beide Funktionsgleichungen. Um die x-Koordinate vom Schnittpunkt zu berechnen, muss man beide Geradengleichungen gleich setzen. Die Lösung der linearen Gleichung liefert dadurch die x-Koordinate vom Geradenschnittpunkt. Setzt man die x-Koordinate in einer der beiden Funktionsgleichungen ein, so ist danach das Ergebnis die y-Koordinate des Schnittpunktes. Damit sind die Koordinaten des Geradenschnittpunktes S eindeutig bestimmt. Dabei ist es egal, in welche der beiden Funktionsgleichungen man die x-Koordinate einsetzt. Man sollte die Gleichung nehmen, mit der sich am einfachsten rechnen lässt. Z. B. wenn in ihr keine Brüche vorkommen. Wenn man das Ergebnis kontrollieren will, muss man die x-Koordinate vom Geradenschnittpunkt in beide Funktionsgleichungen einsetzen. In beiden Fällen muss der Wert der y-Koordinate herauskommen.
1.
2.
3.
4.
5.
6.
2. Teil: Eine Funktionsgleichung und ein Punkt der anderen Geraden
Gegeben ist die Funktionsgleichung einer Geraden g1(x).
Bestimme die Funktionsgleichung der zu g1(x) senkrecht verlaufenden Geraden, wenn diese durch den Punkt P1 verläuft. Berechne danach die Funktionsgleichung der zweiten Geraden. Zeichne schließlich beide Geraden in ein Koordinatensystem.
Tipps zum Vorgehen anhand eines Beispiels beim 2. Teil:
Vorgehensweise:
Die Steigung der zu g1(x) senkrechten Geraden ist der negativ- reziproke Wert des Steigungsfaktors der Geraden g1(x). Das bedeutet: Die Steigung der zu g1(x) senkrechten Geraden findet man, indem man den Kehrwert ihres Steigungsfaktors bildet und mit -1 multipliziert. Sollte der Steigungsfaktor von g1(x) eine ganze Zahl sein, dann muss man daraus einen Bruch bilden, indem man die Zahl mit dem Nenner 1 versieht. In die allgemeine Form der Funktionsgleichung einer linearen Funktion trägt man den Steigungsfaktor a12 der zu g1(x) senkrecht verlaufenden Geraden g2(x) ein. Mit den Koordinaten des vorgegebenen Punktes kann man die Konstante a0 berechnen. Statt senkrecht zueinander verlaufende Geraden sagt man mit anderen Worten die Geraden sind orthogonal.
7.
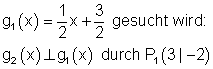
8.
9.
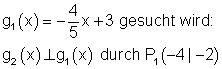
10.
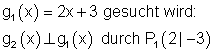
Dazu findest du hier die Lösungen mit ausführlichen Beispielen zu den Aufgaben.
Und hier weitere Aufgaben Lineare Funktionen Aufgaben XVIII Textaufgaben.
Theorie hierzu: Einführung lineare Funktionen.
Lösungsstrategieen bei linearen Funktionen.
Hier eine Übersicht über weitere Beiträge zu linearen Funktionen, darin auch Links zu weiteren Aufgaben.
