Ich habe ja in mehreren Beiträgen Lösungsstrategieen bei linearen Funktionen vorgestellt: lineare Funktionsgleichungen aufstellen und Schnittpunkt zweier Geraden. In diesem Beitrag stelle ich ein paar praktische Tipps hierzu vor. Ich stelle verschiedene Fälle vor, zum Beispiel sind mal die Steigung und ein Punkt bekannt, mal zwei Punkte. Wir wollen jeweils die Funktionsgleichung berechnen.
Lineare Funktionen können bei folgenden Möglichkeiten auftreten:
Fall I:
die Steigung a1 sowie ein Punkt P1 einer Geraden sind bekannt und wir wollen die Funktionsgleichung berechnen.
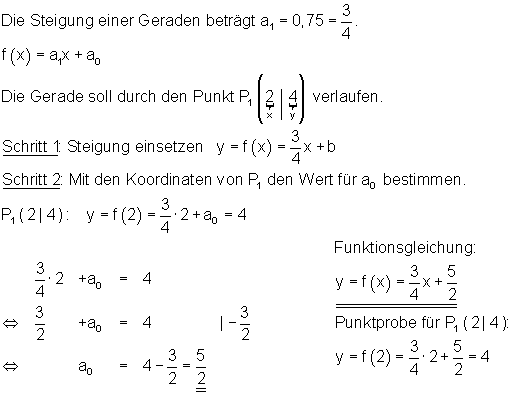
Hier findest du Trainingsaufgaben Funktionsgleichungen aufstellen hierzu (Aufgaben 1 bis 4).
Fall II:
zwei Punkte P1 und P2 bekannt sind und wir wollen die Funktionsgleichung berechnen.
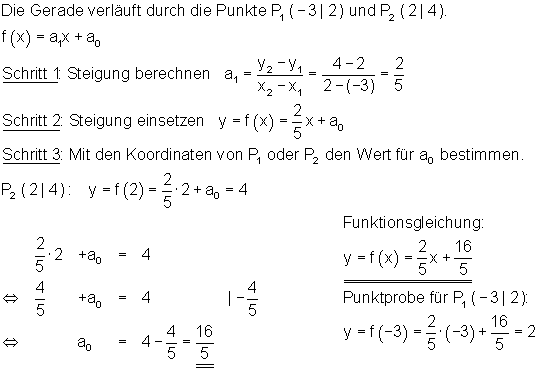
Hier findest du Trainingsaufgaben Funktionsgleichungen aufstellen hierzu (Aufgaben 5 bis 10).
Fall III:
die Achsenschnittpunkte Py und Px einer Geraden sind bekannt und wir wollen die Funktionsgleichung berechnen.

Fall IV:
der Schnittpunkt S zweier Geraden sind bekannt und wir wollen die Funktionsgleichung berechnen.
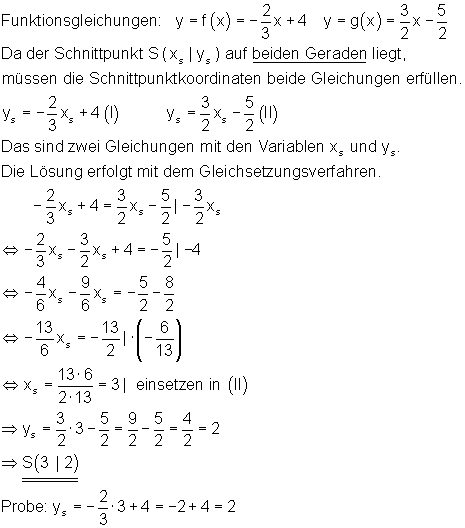
Fall V:
Von einer zu f(x) senkrecht verlaufenden Geraden ist der Punkt P1 bekannt. Wir wollen die Funktionsgleichung g(x) berechnen.
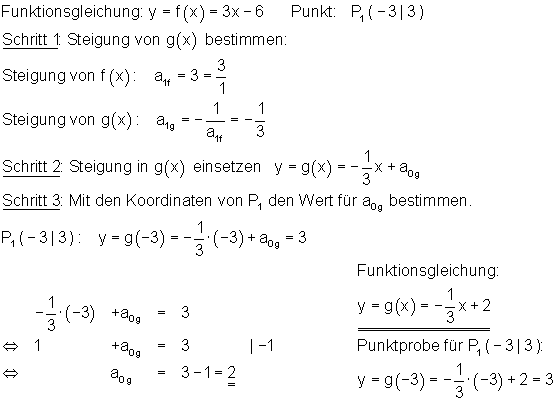
Fall VI:
Wir wollen aus dem Text einer Sachaufgabe die Funktionsgleichung aufstellen.
Hierzu gibt es kein bestimmtes Verfahren. Die Lösung solcher Aufgaben erfordert viel Übung und etwas Geschick. Hier ist logisches Denken die Voraussetzung dafür, den richtigen Ansatz zu finden. Ist der Ansatz erst gefunden, dann lässt sich die Aufgabe fast immer mit einem oder mehreren der oben beschriebenen Verfahren lösen.
Beispiel 1:
Silvia bekommt nach bestandener Führerscheinprüfung von ihrer Tante 2510 € geschenkt. Ihr Traumauto kostet 6500 €. Sie kann monatlich 210 € zurücklegen. Nach welcher Zeit hat sie das Geld für den Autokauf zusammen? Der Ansatz erfolgt ähnlich wie in Beispiel 1 gezeigt.

Beispiel 2:
Wenn Lea 100 Minuten im Monat mit dem Handy telefoniert, zahlt sie 18 €. Telefoniert sie 200 Minuten, so hat sie 26 € zu zahlen. Wie hoch ist die Grundgebühr, was kostet 1 Minute telefonieren.
Ansatz: Die Grundgebühren fallen immer an. Dazu kommen Kosten für die Zeit, die telefoniert wird. Diese Kosten sind proportional zur Gesprächszeit.

Dazu findest du hier Aufgaben Lineare Funktionen Aufgaben XVIII Textaufgaben.
Außerdem hier habe ich die Vorgehensweise erklärt: Lösung alltäglicher Probleme mittels linearer Funktionen.
Hier findest du eine Übersicht über weitere Beiträge zu linearen Funktionen,


