Lineare Funktionen kurz erklärt

Hier stelle ich einen Lernzettel zu linearen Funktionen zusammen. Dabei zeige ich, wie man die Achsenschnittpunkte, das Steigungsdreieck einer linearen Funktion berechnet und wie man Lineare Funktionen aus gegebenen Bedingungen aufstellt. Außerdem erkläre ich die Lage zweier Geraden zueinander. Schließlich stelle ich ein interaktives Programm zu Erkennen von Geraden zur Verfügung.

Allgemeine Funktionsgleichung der Geraden einer linearen Funktion

Achsenschnittpunkte einer linearen Funktion

siehe auch Einfuehrung in lineare Funktionen

Das Steigungsdreieck einer linearen Funktion

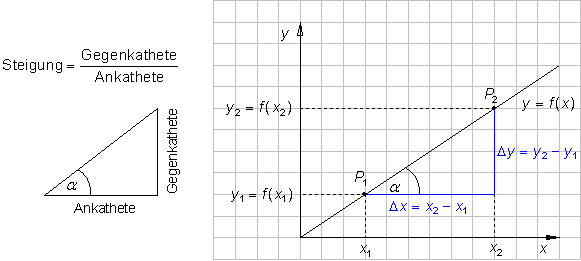
Steigung einer Geraden durch die Punkte P₁ ( x₁ | y₁ ) und P₂ ( x₂ | y₂ )

 

Lineare Funktionen aus gegebenen Bedingungen aufstellen

1. Steigung und ein Punkt sind bekannt

Eine Gerade mit der Steigung a₁ verläuft durch den Punkt P₁( x₁ | y₁ ).

Beispiel:

Allgemeine Lösung:

 

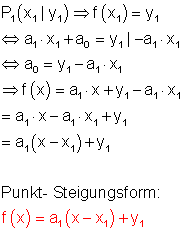
2. Zwei Punkte sind bekannt

Zwei Punkte P₁( x₁ | y₁ ) und P₂( x₂ | y₂ ) liegen auf einer Geraden.

Beispiel:

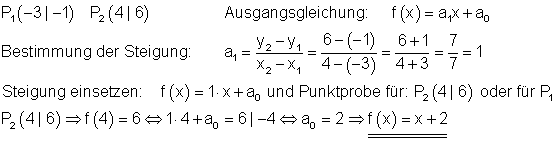
Oder die allgemeine Form der Geradengleichung durch zwei Punkte verwenden.

siehe auch Lineare Funktionen aus gegebenen Bedingungen

Sonderfälle für Geradengleichungen.

Parallele zur x- Achse im Abstand a₀:

Parallele zur y- Achse im Abstand a:

siehe auch Lineare Funktionen aus gegebenen Bedingungen

Dazu kannst du dir auch dieses 📽️Linieare Funktion aus 2 Punkten aufstellen ansehen.

Lage zweier Geraden zueinander

Zwei Geraden f und g können sich schneiden, parallel zueinander oder identisch sein.
Lösungsansatz durch Gleichsetzen der Funktionsgleichungen f(x) = g(x).Hat f(x) = g(x) genau eine Lösung, dann schneiden sich die Graphen von f und g in einem Punkt. Die Geraden haben unterschiedliche Steigungen.
Hat f(x) = g(x) keine Lösung, dann haben beide Geraden keinen gemeinsamen Punkt. Sie verlaufen parallel zueinander.
Hat f(x) = g(x) unendlich viele Lösungen, dann sind beide Geraden identisch.
Orthogonale Geraden (zwei Geraden stehen senkrecht aufeinander).
Für die Steigung zweier senkrecht aufeinander stehender Geraden g und h gilt:

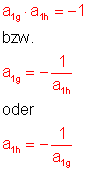
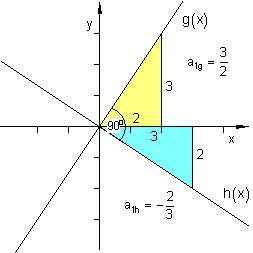
siehe auch Lage zweier Geraden zueinander

Geraden erkennen Interaktiv: Klicken Sie auf den Start-Knopf. Dann erscheint eine Gerade. Geben Sie den dazugerhörigen Term ein und klicken Sie auf weiter. Daraufhin sehen Sie, ob Sie richtig lagen. Wenn Sie dies 10 Mal durchaufen haben, bekommen Sie eine Note.

Hier finden Sie Aufgaben Lineare Funktionen Aufgaben XVIII Textaufgaben.

Und hier eine Übersicht über weitere Beiträge zu linearen Funktionen,  dort auch Links zu weiteren Aufgaben.