In diesem Beitrag führe ich in die Aussagelogik ein. Zuerst definiere ich die Begriffe Aussagen und Aussageformen in der Mathematik. Dazu gebe ich viele anschauliche Beispiele zu Bestimmungsgleichung und Wahrheitsgehalt einer Aussage. Im folgenden Beiträgen werde ich mich mit deren Verknüpfungen beschäftigen.
Definition Aussagen
In der Mathematik spricht man von Aussagen, wenn für einen Sachverhalt entschieden werden kann, ob er wahr oder falsch ist. Dieser Sachverhalt wird meist in Form eines Satzes dargestellt, kann aber auch rein mathematisch durch Gleichungen oder Ungleichungen angegeben werden.
Hier Beispiele für Aussagen in Form von Sätzen:
A: Brüssel ist die Hauptstadt von Belgien.
B: Moskau ist die Hauptstadt von China.
Die Aussage A ist wahr. Mit anderen Worten: der Wahrheitsgehalt von A ist wahr.
Die Aussage B dagegen ist falsch. Mit anderen Worten: der Wahrheitsgehalt von B ist falsch.
Dies schreiben wir in Kurzform: w(A) = W und w(B) = F
Und mathematisch schreiben wir dies so:
| A: 12 < 7 | w(A) = F |
| B: 3 + 4 = 7 | w(A) = W |
Aussage: Eine Aussage ist also ein Sachverhalt, dessen Wahrheitsgehalt eindeutig bestimmbar ist.
Keine Aussagen im Sinne der Definition dagegen sind:
- Guten Tag
- Lieben Sie Brahms?
- Nachts ist es kälter als draußen
Definition Aussageformen
Treten in einer Aussage Variable (Platzhalter) auf und lässt sich der Wahrheitsgehalt nur durch Einsetzen geeigneter Begriffe feststellen, dann spricht man von Aussageformen.
Zum Beispiel:

Bestimmungsgleichung Beispiel:
Eine Bestimmungsgleichung ist eine Aussageform A(x). Durch Einsetzen einer Zahl für den Platzhalter x kann der Wahrheitsgehalt der Aussage ermittelt werden.
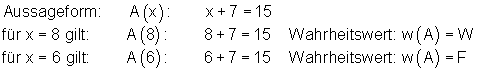
Merke:
Eine Aussageform ist ein Sachverhalt, der mindestens eine Variable enthält und durch Einsetzen geeigneter Begriffe anstelle des Platzhalters zu einer Aussage führt.
Übung:


Lösung zu 1:
![]()
Lösung zu 2:
a) A: Rom ist die Hauptstadt von Italien.
b) B: 7 ist kleiner als 25.
c) C: Mathematik und Englisch sind Fächer unseres Stundenplans.
d) D: 4 ist doppelt so groß wie 2
Eine Übersicht über alle mathematischen Zeichen findest du hier.
Im nächsten Beitrag werden wir dann sehen, wie man Aussagen verknüpft.
Hier gibt es eine Übersicht über alle Beiträge und Aufgaben zum Thema Aussagen und Mengen.


