In diesem Beitrag stelle ich ein Übersicht der Verknüpfung von Aussagen in der Mathematik zusammen: Konjunktion (und), Disjunktion (oder), Implikation (wenn … dann), Äquivalenz (genau wenn … dann), Negation (nicht). Außerdem stelle ich viele Beispielen und Übungen zur Verfügung. Zuletzt fasse ich alles übersichtlich zusammen.
Konjunktion
„Und“-Verknüpfung (Konjunktion)
Werden Aussagen miteinander verknüpft, so entstehen zusammengesetzte Aussagen, deren Wahrheitsgehalt in der angegebenen Verbindung wieder überprüft werden kann. Hierzu ein Beispiel aus dem Alltag:
Eine Tresor ist durch zwei Schlösser gesichert.
Wie bekommen wir ihn auf? Welche Bedingung muss erfüllt sein?
Die Tresortür lässt sich nur öffnen, wenn beide Schlösser geöffnet werden.
Bedingung: Schloss 1 und Schloss 2 müssen geöffnet sein.
Definition Konjunktion:
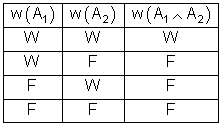
Sind zwei Aussagen A1 und A2 so miteinander verknüpft, dass die zusammengesetzte Aussage nur dann wahr ist, wenn sowohl A1 als auch A2 wahr ist, so heißt diese Verknüpfung Konjunktion.
![]()
1. Beispiel:

2. Beispiel:
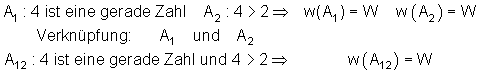
3. Beispiel:

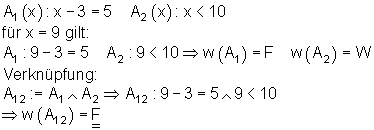
Merke:
Die Konjunktion zweier Aussagen A1 und A2 ist nur dann wahr, wenn beide Aussagen wahr sind.
Übung:
Gib den Wahrheitsgehalt der Konjunktion an:
a) A: München liegt an der Isar und Köln liegt am Rhein.
b) B: Heute ist Montag und die Sonne scheint.
c) C: Manchmal regnet es und manche Schüler lieben Mathematik.
d) D: 4 ist eine gerade Zahl und größer als 7.
Lösung:

Die „Oder“ – Verknüpfung (Disjunktion)
Der Tresor ist für Unbefugte schon dann nicht zu öffnen, wenn eins der beiden Schlösser geschlossen ist, also Schloss 1 oder Schloss 2. Beide Schlösser erhöhen die Sicherheit.
Definition Disjunktion:
Sind zwei Aussagen A1 und A2 so miteinander verknüpft, dass die zusammengesetzte Aussage immer dann wahr ist, wenn entweder die eine oder die andere oder beide Aussagen wahr sind, so heißt diese Verknüpfung Disjunktion.
![]()
4. Beispiel:

5. Beispiel:
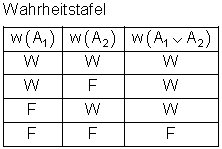
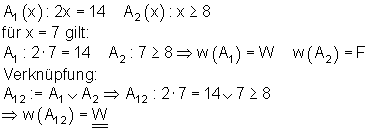
Merke:
Die Disjunktion zweier Aussagen A1 und A2 ist nur dann wahr, wenn mindestens eine der beiden Aussagen wahr ist.
Übung:
Gib den Wahrheitsgehalt der Disjunktion an:
a) A: München liegt an der Isar oder Köln liegt am Rhein.
b) B: Heute ist Montag oder die Sonne scheint.
c) C: Heute regnet es oder manche Schüler lieben Mathematik.
d) D: 4 ist eine gerade Zahl oder größer als 7.
Lösung:
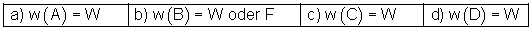
Die Implikation
Verknüpfungszeichen wenn … dann ->
Definition Implikation:
Sind zwei Aussagen A1 und A2 so miteinander verknüpft, dass aus der Aussage A1 die Aussage A2 logisch folgt, so heißt diese Verknüpfung Implikation.
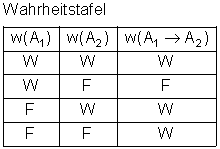
Merke:
Die Implikation zweier Aussagen A1 und A2 ist genau dann falsch, wenn A1 wahr und A2 falsch ist. In allen anderen Fällen ist sie wahr.
Die Äquivalenz
Verknüpfungszeichen genau wenn … dann <=>
Definition Äquivalenz:
Die wechselseitige Implikation heißt Bijunktion oder Äquivalenz
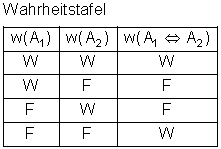
Die Wahrheitstafel entspricht der Implikation, dabei können die Aussagen A1 und A2 jedoch vertauscht werden. Die Verknüpfung der beiden Aussagen über die Äquivalenz führt genau dann zu einer wahren Aussage, wenn der Wahrheitsgehalt beider Aussagen gleich (äquivalent) ist.
6. Beispiel:

Die Negation
![]()
Definition Negation:
Die Negation einer Aussage ist immer dann wahr, wenn die Aussage falsch ist, und immer dann falsch, wenn die Aussage wahr ist
Beispiel:


Die doppelte Negation einer Aussage führt wieder zur ursprünglichen Aussage.
7. Beispiel:

Zusammenfassung
Konjunktion:
Disjunktion
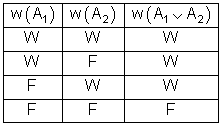
Implikation
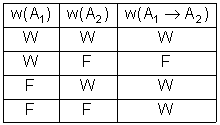
Äquivalenz
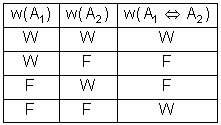
Negation
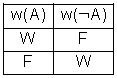
Eine Übersicht über alle mathematischen Zeichen finden Sie hier
Hier findest du eine Übersicht über alle Beiträge und Aufgaben zum Thema Aussagen und Mengen, darin auch Links zu Aufgaben.


