In diesem Beitrag geht es zuerst um den Betrag eines Vektors. Danach um die Berechnung des Richtungskosinus.
Betrag eines Vektors berechnen
Diesmal soll der Betrag eines Vektors berechnet werden, wenn dieser in Komponenten oder Koordinatenschreibweise gegeben ist. 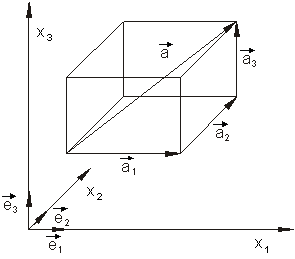
Wenn wir die obige Darstellung betrachten, erkennen wir, dass der Vektor
\overrightarrow{a} = \overrightarrow{a_1} + \overrightarrow{a_2} + \overrightarrow{a_3} = a_1\overrightarrow{e_1} + a_2\overrightarrow{e_2} + a_2\overrightarrow{e_3}
die gerichtete Raumdiagonale eines Quaders ist, dessen Kantenlängen a1, a2, und a3 sind.
Daher stimmt der Betrag des Vektors mit der Länge der Raumdiagonalen überein.
Nach Anwendung des Satzes vom Pythagoras erhält man für den Betrag des Vektors:
\overrightarrow{a} = a_1\overrightarrow{e_1} + a_2\overrightarrow{e_2} +a_3\overrightarrow{e_3}
Betrag: \, \mid \overrightarrow{a} \mid = a = \sqrt{a_1\,^2 + a_2\,^2 + a_3\,^2}
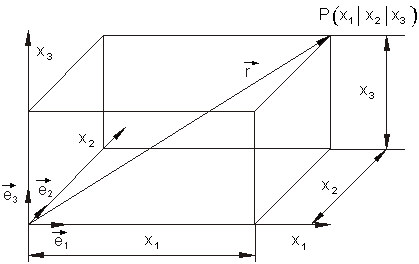
Wenn der Vektor als Ortsvektor vorliegt, dann gilt:
\overrightarrow{r} = x_1\overrightarrow{e_1} + x_2\overrightarrow{e_2} + x_3\overrightarrow{e_3}
\mid \overrightarrow{r} \mid = r = \sqrt{x_1\,^2 + x_2\,^2 + x_3\,^2}
Beispiel:
\overrightarrow{r} =\begin{pmatrix} 2 \\ 3 \\ 1 \end{pmatrix}\Rightarrow \mid \overrightarrow{r} \mid = \sqrt{2^2 + 3^2 + 1^2}
= \sqrt{4 + 9 + 1}
= \sqrt{14} \approx 3,742
Den Richtungskosinus eines Vektors bestimmen
Zur Bestimmung der Richtung, in die ein in Komponenten bzw. Koordinatenform gegebener Vektor im Raum zeigt, verwendet man die Winkel, die dieser Vektor mit den Einheitsvektoren bildet.
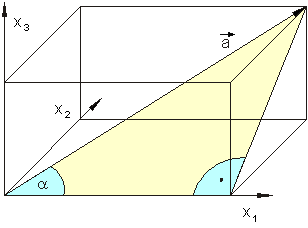
Der Winkel, den die Raumdiagonale bzw. der Diagonalvektor mit der x1-Achse und damit auch mit deren Einheitsvektor bildet, liegt in einem Dreieck, das durch die Raumdiagonale, die Flächendiagonale der rechten Seitenfläche des Quaders sowie die x1-Komponente des Diagonalvektors gebildet wird. Dieses Dreieck ist rechtwinklig, so dass gilt:
\cos(\alpha) = \dfrac{a_1}{\mid \overrightarrow{a} \mid} = \dfrac{x_1}{\mid \overrightarrow{a} \mid}
Analoge Beziehungen erhält man auch für die anderen beiden Winkel, so dass man schreiben kann:
\cos(\alpha) = \dfrac{a_1}{\mid \overrightarrow{a} \mid} = \dfrac{x_1}{\mid \overrightarrow{a} \mid}
\cos(\beta) = \dfrac{a_2}{\mid \overrightarrow{a} \mid} = \dfrac{x_2}{\mid \overrightarrow{a} \mid}
\cos(\gamma) = \dfrac{a_3}{\mid \overrightarrow{a} \mid} = \dfrac{x_3}{\mid \overrightarrow{a} \mid}
Die Funktionswerte der Kosinus der drei Winkel werden Richtungskosinus des Vektors genannt.
Für die Summe der drei Richtungskosinus gilt:
\cos^2(\alpha) + \cos^2(\beta) + \cos^2(\gamma) = 1
Das bedeutet:
Die Quadratsumme der Richtungskosinus ist immer 1.
Dieser Zusammenhang lässt sich leicht durch eine einfache Rechnung zeigen:
\cos^2(\alpha) + \cos^2(\beta) + \cos^2(\gamma) = \dfrac{a_1\,^2}{\mid \overrightarrow{a} \mid^2} + \dfrac{a_2\,^2}{\mid \overrightarrow{a} \mid^2} + \dfrac{a_3\,^2}{\mid \overrightarrow{a} \mid^2}
= \dfrac{a_1\,^2 + a_2\,^2 + a_3\,^2}{\mid \overrightarrow{a} \mid^2}
Mit \mid \overrightarrow{a} \mid^2 = ( \sqrt{a_1\,^2 + a_2\,^2 + a_3\,^2} )^2 = a_1\,^2 + a_2\,^2 + a_3\,^2 wird daraus
\dfrac{a_1\,^2 + a_2\,^2 + a_3\,^2}{a_1\,^2 + a_2\,^2 + a_3\,^2} = 1
Aus \cos(\alpha) = \dfrac{a_1}{\mid \overrightarrow{a}\mid}, \, \cos(\beta) = \dfrac{a_2}{\mid \overrightarrow{a}\mid}, \, \cos(\alpha) = \dfrac{a_3}{\mid \overrightarrow{a}\mid}
folgt für die Koordinaten des Vektors \overrightarrow{a}:
a_1 = \mid \overrightarrow{a} \cos(\alpha), \, a_2 = \mid \overrightarrow{a} \cos(\beta), \, a_3 = \mid \overrightarrow{a} \cos(\gamma)
Damit ist es nun möglich einen Vektor mit Hilfe seiner Bestimmungsgrößen Betrag und Richtung zu schreiben:
\overrightarrow{a} = a_1\overrightarrow{e_1} + a_2\overrightarrow{e_2} + a_3\overrightarrow{e_3} = \mid \overrightarrow{a} \mid \cos(\alpha) \overrightarrow{e_1} + \mid \overrightarrow{a} \mid \cos(\beta) \overrightarrow{e_2} + \mid \overrightarrow{a} \mid \cos(\gamma) \overrightarrow{e_3}
\mid \overrightarrow{a} \mid wird ausgeklammert und beide Seiten werden durch \mid \overrightarrow{a} \mid dividiert.
\Rightarrow \overrightarrow{a} = \mid \overrightarrow{a} \mid ( \cos(\alpha) \overrightarrow{e_1} + \cos(\beta) \overrightarrow{e_2} + \cos(\gamma) \overrightarrow{e_3}) \, \Big| : \mid \overrightarrow{a} \mid
\Leftrightarrow \dfrac{\overrightarrow{a}}{\mid \overrightarrow{a} \mid} = \overrightarrow{a_e} = \cos(\alpha)\overrightarrow{e_1} + \cos(\beta)\overrightarrow{e_2} + \cos(\gamma)\overrightarrow{e_3} = \begin{pmatrix} \cos(\alpha) \\ \cos(\beta) \\ \cos(\gamma) \end{pmatrix}
Merke:
Die Koordinaten eines Einheitsvektors sind seine Richtungskosinus.
\overrightarrow{a_e} = \cos(\alpha)\overrightarrow{e_1} + \cos(\beta)\overrightarrow{e_2} + \cos(\gamma)\overrightarrow{e_3} = \begin{pmatrix} \cos(\alpha) \\ \cos(\beta) \\ \cos(\gamma) \end{pmatrix} mit \mid \overrightarrow{a_e} \mid = 1
.
Berechnungsbeispiele
Beispiel 1
Für folgende Vektoren sollen die Beträge und die Richtungskosinus berechnet werden:
a) \overrightarrow{a} = 4\overrightarrow{e_1} + 3\overrightarrow{e_2} + 2\overrightarrow{e_3} = \begin{pmatrix} 4 \\ 3 \\ 2 \end{pmatrix}
b) \overrightarrow{b} = 2\overrightarrow{e_1} - 3\overrightarrow{e_2} - 1\overrightarrow{e_3} = \begin{pmatrix} 2 \\ -3 \\ -1 \end{pmatrix}
Die Ergebnisse sind mit einer Genauigkeit von drei Stellen hinter dem Komma anzugeben.
Lösung: a)
Betrag:
\mid \overrightarrow{a} \mid = a = \sqrt{a_1\,^2 + a_2\,^2 + a_3\,^2}
= \sqrt{4^2 + 3^2 + 2^2}
= \sqrt{16 + 9 + 4}
= \underline{\underline{\sqrt{29} \approx 5,385}}
Der Vektor hat eine Länge von etwa 5,385 LE.
Richtungskosinus:
\cos(\alpha) = \dfrac{a_1}{\mid \overrightarrow{a} \mid} = \dfrac{a_1}{a} = \dfrac{4}{\sqrt{29}} \approx 0,743 \Rightarrow \underline{\underline{\alpha \approx 42,031°}} \newline
\cos(\beta) = \dfrac{a_2}{\mid \overrightarrow{a} \mid} = \dfrac{a_2}{a} = \dfrac{3}{\sqrt{29}} \approx 0,557 \Rightarrow \underline{\underline{\beta \approx 56,145°}} \newline
\cos(\gamma) = \dfrac{a_3}{\mid \overrightarrow{a} \mid} = \dfrac{a_3}{a} = \dfrac{2}{\sqrt{29}} \approx 0,317 \Rightarrow \underline{\underline{\gamma \approx 68,199°}}
Lösung: b)
Betrag:
\mid \overrightarrow{b} \mid = b = \sqrt{b_1\,^2 + b_2\,^2 + b_3\,^2}
= \sqrt{2^2 + (-3)^2 + (-1)^2} \\ = \sqrt{4 + 9 + 1}
= \underline{\underline{\sqrt{14} \approx 3,742}}
Der Vektor hat eine Länge von etwa 3,742 LE.
Richtungskosinus:
\cos(\alpha) = \dfrac{b_1}{\mid \overrightarrow{b} \mid} = \dfrac{b_1}{b} = \dfrac{2}{\sqrt{14}} \approx 0,535 \Rightarrow \underline{\underline{\alpha \approx 57,688°}}\newline
\cos(\beta) = \dfrac{b_2}{\mid \overrightarrow{b} \mid} = \dfrac{b_2}{b} = \dfrac{-3}{\sqrt{14}} \approx -0,802 \Rightarrow \underline{\underline{\beta \approx 143,301°}}\newline
\cos(\gamma) = \dfrac{b_3}{\mid \overrightarrow{b} \mid} = \dfrac{b_3}{b} = \dfrac{-1}{\sqrt{14}} \approx -0,267 \Rightarrow \underline{\underline{\gamma \approx 105,501°}}
Merke:
Ist der Kosinus eines Winkels negativ, dann liegt der Wert des Winkels zwischen 90° und 180°.
Beispiel 2
Gesucht ist der Ortsvektor von der Länge 2, der mit der x1 – Achse einen Winkel von 60°, mit der x2-Achse einen Winkel von 135° und mit der x3-Achse einen spitzen Winkel einschließt.
Lösung:
Ortsvektor
\overrightarrow{r} mit der Länge 2 bedeutet \overrightarrow{r} = 2 \newline
\alpha = 60° \Rightarrow \cos(\alpha) = \cos(60°) = dfrac{1}{2}, \,\,\, \beta = 135° \Rightarrow \cos(\beta) = \cos(135°) = - \dfrac{1}{2} \sqrt{2} \newline
\cos^2(\alpha) + \cos^2(\beta) + \cos^2(\gamma) = 1 \Leftrightarrow \cos(\gamma) = \pm \sqrt{1 - \cos^2(\alpha) - \cos^2(\beta)} \newline
\Leftrightarrow \cos(\gamma) = \pm \sqrt{1-(\dfrac{1}{2})^2 - (- \dfrac{1}{2} \sqrt{2})^2} = \pm \sqrt{1 - \dfrac{1}{4} - \dfrac{1}{2}} = \pm \sqrt{\dfrac{1}{4}} = \pm \dfrac{1}{2} \newline
da \gamma spitz sein soll, gilt:
\cos(\gamma) = \dfrac{1}{2} \Rightarrow \gamma = 60° \newline
Der Einheitsvektor ist: \overrightarrow{e_1} = \cos[\alpha)\overrightarrow{e_1} + \cos[\beta)\overrightarrow{e_2} + \cos[\gamma)\overrightarrow{e_3}
= \cos(60°)\overrightarrow{e_1} + \cos(135°)\overrightarrow{e_2} + \cos(60°)\overrightarrow{e_3} = \dfrac{1}{2} \overrightarrow{e1} - \dfrac{1}{2}\sqrt{2} \overrightarrow{e2} + \dfrac{1}{2} \overrightarrow{e3} \newline
und der Vektor selbst:
\overrightarrow{r} = \mid \overrightarrow{r} \mid \overrightarrow{e_r} = 2(\dfrac{1}{2} \overrightarrow{e_1} - \dfrac{1}{2}\sqrt{2} \overrightarrow{e2} + \dfrac{1}{2} \overrightarrow{e3}) \newline
\Leftrightarrow \underline{\underline{\overrightarrow{r} = \overrightarrow{e_1} - \sqrt{2} \overrightarrow{e_2} + \overrightarrow{e_3}}}
Zusammenfassung
Betrag eines Vektors, Betrag eines Ortsvektors:
\overrightarrow{a} = a_1\overrightarrow{e_1} + a_2\overrightarrow{e_2} + a_3\overrightarrow{e_3} = \begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix} \Rightarrow \mid \overrightarrow{a} \mid = a = \sqrt{a_1\,^2 + a_2\,^2 + a_3\,^2} \newline
\overrightarrow{r} = x_1\overrightarrow{e_1} + x_2\overrightarrow{e_2} + x_3\overrightarrow{e_3} = \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} \Rightarrow \mid \overrightarrow{r} \mid = \sqrt{x_1\,^2 + x_2\,^2 + x_3\,^2}
Richtungskosinus eines Vektors
\cos[\alpha] = \dfrac{a_1}{\mid \overrightarrow{a} \mid} = \dfrac{x_1}{\mid \overrightarrow{a} \mid}, \, \cos[\beta] = \dfrac{a_2}{\mid \overrightarrow{a} \mid} = \dfrac{x_2}{\mid \overrightarrow{a} \mid}, \, \cos[\gamma] = \dfrac{a_3}{\mid \overrightarrow{a} \mid} = \dfrac{x_3}{\mid \overrightarrow{a} \mid} \newline
Es gilt:
\cos^2(\alpha) + \cos^2(\beta) + \cos(\gamma) = 1
Koordinaten des Einheitsvektors:
Die Koordinaten eines Einheitsvektors sind seine Richtungskosinus.
\overrightarrow{a_e} = \cos(\alpha)\overrightarrow{e_1} + \cos(\beta)\overrightarrow{e_2} + \cos(\gamma)\overrightarrow{e_3} = \begin{pmatrix} \cos(\alpha) \\ \cos(\beta) \\ \cos(\gamma) \end{pmatrix} mit \mid \overrightarrow{a_e} \mid = 1 .
Hier findest du eine Übersicht über alle Beiträge und Aufgaben zum Thema Vektorrechnung.


