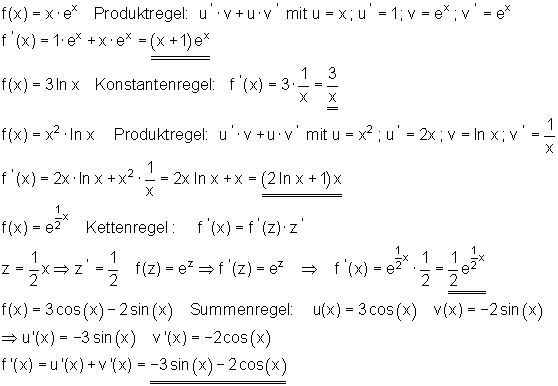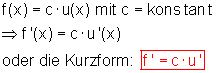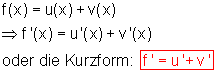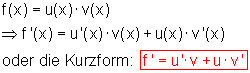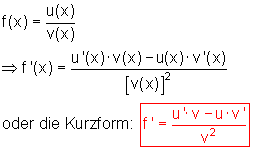Nachdem ich in den letzten Beiträgen mit anschaulichen Beispielen aus der Praxis in die Differentialrechnung eingeführt habe, erkläre ich hier die Differentiationsregeln: Produktregel, Quotientenregel, Kettenregel. Zuerst wiederhole ich einige Regeln aus den Grundlagen der Mathematik: Potenzregel, Konstantenregel, Summenregel. Anschließend fasse ich die wichtigsten Formeln zusammen.
- Potenzregel, Konstantenregel und Summenregel
- Produktregel Differentation
- Quotientenregel
- Kettenregel
- Zusammenfassung der wichtigsten Formeln
- Ableitung weiterer Funktionenklassen
Bisher bekannte Regeln
Potenzregel
1.) Alten Exponenten als Faktor vor die Variable x setzen.
2.) Neuer Exponent ist alter Exponent vermindert um eins
Konstantenregel
Wenn eine Funktion aus einer elementaren Funktion multipliziert mit einer Konstanten zusammengesetzt ist, dann ist die Ableitung dieser Funktion gleich der Ableitung der Elementarfunktion multipliziert mit der Konstanten.
f(x) =c \cdot u(x) \quad mit \quad c = konstant \\ \Rightarrow f'(x) = c \cdot u'(x)Summenregel
Wenn eine Funktion aus der Summe zweier Funktionen zusammengesetzt ist,
dann ist die Ableitung der Funktion gleich der Summe der Ableitungen der einzelnen Funktionen.
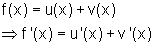
Dazu kannst du dir das 📽️Video Differentiationsregeln: Potenzregel, Konstantenregel, Summenregel ansehen.
Differentiationsregeln
Produktregel Differentation
Wenn eine Funktion aus dem Produkt zweier Einzelfunktionen zusammengesetzt ist,
dann wird die Ableitung wie folgt gebildet:
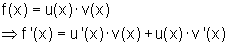
Der Beweis ist etwas aufwendiger, deshalb verzichtet ich an dieser Stelle darauf .
1. Beispiel:
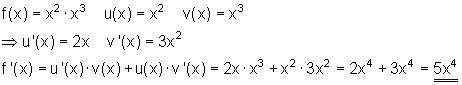
In diesem Fall könnten wir f(x) auch mithilfe der Potenzgesetze vereinfachen:
f(x)=x^2\cdot x^3 =x^5 \Rightarrow f'(x)=\underline{\underline{5x^4}}
2. Beispiel:
In diesem Fall bietet sich allerdings die Potenzregel an:
f(x) = (x^3 - 2)\cdot (x^2 +2)
u'(x) = 3x^2 \quad v'(x) = 2x
f'(x) = 3x^2 \cdot (x^2 + 2) + (x^3 - 2) \cdot 2x
\Rightarrow f'(x)=3x^4 + 6x^2 +2x^4 -4x
\Rightarrow f'(x)=\underline{\underline{5x^4+6x^2-4x}}
3. Beispiel:
Wenn die beiden Funktionen sehr verschieden sind, bietet sich auch die Potenzregel an.
f(x)= x^2 \cdot sin(x)
Dazu kannst du dir das 📽️Video Produktregel ansehen.
Quotientenregel
Wenn eine Funktion aus den Quotienten zweier Funktionen u(x) und v(x) zusammengesetzt ist,
dann wird die Ableitung der Funktion wie folgt gebildet:
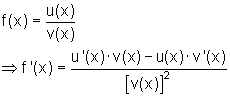
Beweis:
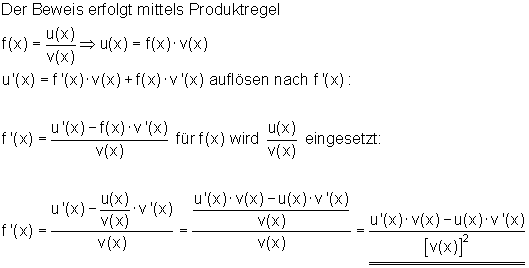
Beispiel:
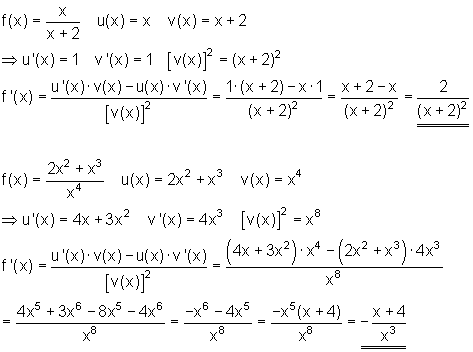
Dazu kannst du dir das 📽️Video Quotientenregel ansehen.
Kettenregel
Sind in einer Funktion die Terme mit der Variablen x so zusammengefasst, dass eine übergeordnete Variable z entsteht, so kann diese Funktion als Funktion einer Funktion betrachtet werden.(Funktionskette).
Dann ist die Ableitung dieser Funktions-kette gleich der äußeren Ableitung multipliziert mit der inneren Ableitung.

Der Beweis ist etwas aufwendiger, deshalb verzichtet ich hier auch darauf .
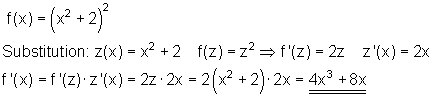
Dazu kannst du dir das 📽️Video Differentiationsregeln Kettenregel ansehen.
Zusammenfassung
Differenzenquotient:
(Sekantensteigung oder mittlere Änderungsrate)
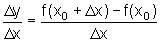
Differentialquotient:
(Tangentensteigung oder momentane Änderungsrate)
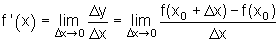
Konstantenregel
Summenregel:
Produktregel:
Quotientenregel:
Kettenregel:
Ableitung weiterer Funktionenklassen
Funktionsgleichung |
Ableitungsfunktionsgleichung |
Beispiele: