In diesem Beitrag erkläre ich, welche Dreiecksarten es gibt. Dazu zeige viele Beispiele.
Definition Dreieck
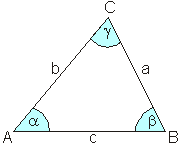
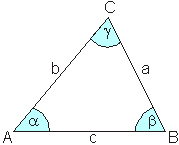
Ein Dreieck hat die Seiten a, b, c und die Winkel 
Die drei Seiten schneiden sich in drei Ecken A, B, C.
Gegenüberliegende Seiten und Ecken werden mit gleichen Buchstaben bezeichnet. Die Bezeichnung erfolgt entgegengesetzt dem Uhrzeigersinn.
Klassifizierung der Dreiecksarten nach Größe der Seiten
In Abhängigkeit von der Größe der Dreiecksseiten unterscheidet man folgende Dreiecksarten:
Definition Ungleichseitiges Dreieck:
Ein Dreieck mit unterschiedlich langen Seiten nennt man ungleichseitiges Dreieck.
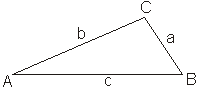
Für die Seiten gilt hierbei: a≠ b ≠ c.
Definition Gleichschenkliges Dreieck:
Ein gleichschenkliges Dreieck ist ein Dreieck mit zwei gleich langen Seiten. Die gleichlangen Seiten nennt man Schenkel, die dritte Seite Basis oder Grundseite.
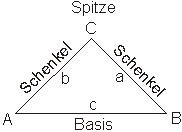
Für die Seiten gilt dabei: a = b ≠ c.
Definition Gleichseitiges Dreieck
Ein gleichseitiges Dreieck ist ein Dreieck, in dem alle Seiten gleich lang sind.
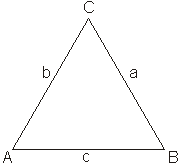
Für diese Seiten gilt diesmal: a = b = c.
Klassifizierung der Dreiecksarten nach Größe der Winkel
In Abhängigkeit von der Größe der Dreieckswinkel unterscheidet man folgende Dreiecksarten:
Definition Spitzwinkliges Dreieck:
Ein spitzwinkliges Dreieck ist ein Dreieck, bei dem alle Winkel kleiner als 900 sind. Die drei Seiten müssen nicht unterschiedlich lang sein.
Für die Winkel gilt: α < 90°, β < 90°, γ < 90°.
Definition Rechtwinkliges Dreieck:
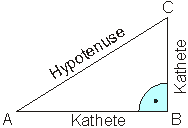
Ein rechtwinkliges Dreieck ist ein Dreieck mit einem rechten Winkel. Die Schenkel, die den rechten Winkel bilden, nennt man Katheten. Die dem rechten Winkel gegenüberliegende Seite ist die Hypotenuse.
Definition Stumpfwinkliges Dreieck:
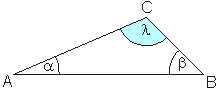
Ein stumpfwinkliges Dreieck ist ein Dreieck mit einem stumpfen Winkel, das heißt mit einem Winkel zwischen 900 und 1800. Dem stumpfen Winkel gegenüber liegt die längste Seite.
Hier findest du eine Übersicht über alle Beiträge zur Geometrie, dort auch Links zu Aufgaben.
