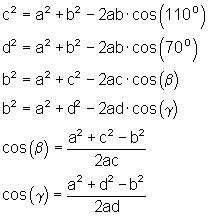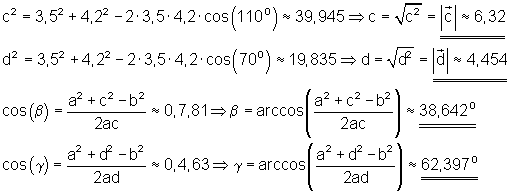Hier findest du die Lösungen der Aufgaben zur Addition und Subtraktion von Vektoren mit komplettem Lösungsweg.
1.a) Ausführliche Lösung:
![]()
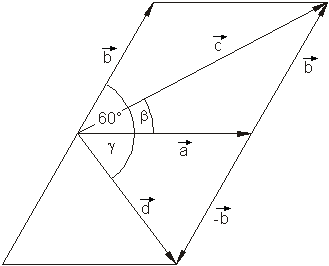
Die zeichnerische Lösung ergibt:
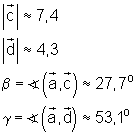
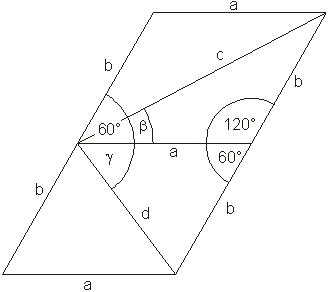
Die rechnerische Lösung erfolgt mit Hilfe des Kosinussatzes.
Ansatz:
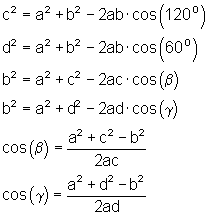
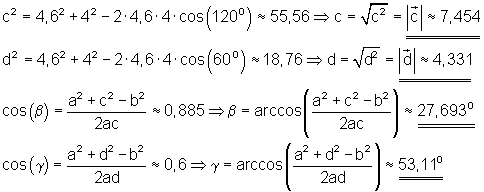
1. b) Ausführliche Lösung:
![]()
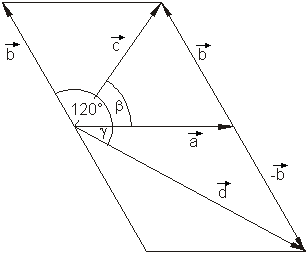
Die zeichnerische Lösung ergibt:
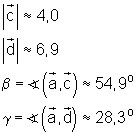
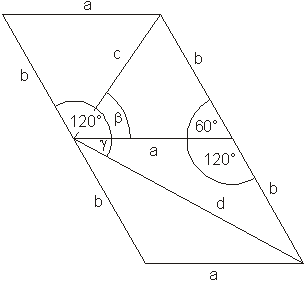
Die rechnerische Lösung erfolgt mit Hilfe des Kosinussatzes.
Ansatz:
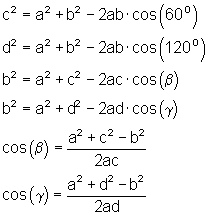
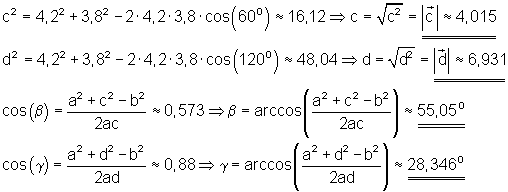
1. c) Ausführliche Lösung:
![]()
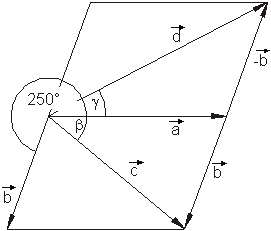
Die zeichnerische Lösung ergibt:
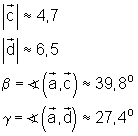
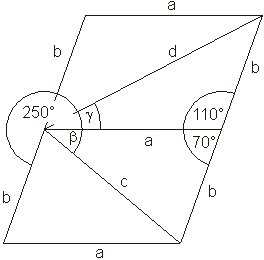
Die rechnerische Lösung erfolgt mit Hilfe des Kosinussatzes.
Ansatz:
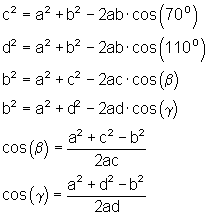
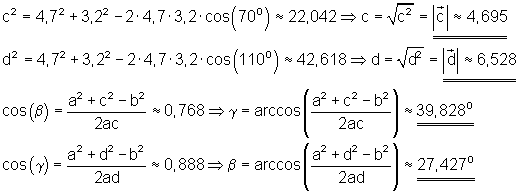
1. d) Ausführliche Lösung:
![]()
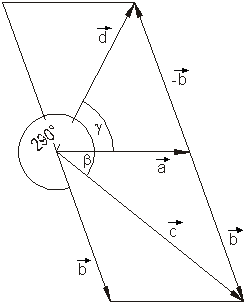
Die zeichnerische Lösung ergibt:
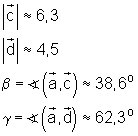
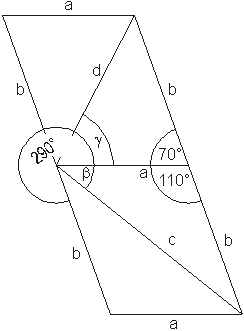
Die rechnerische Lösung erfolgt mit Hilfe des Kosinussatzes.
Ansatz:
2. Ausführliche Lösung:
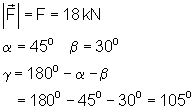
Gerechnet wird mit Beträgen.
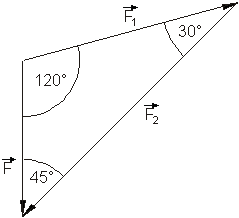
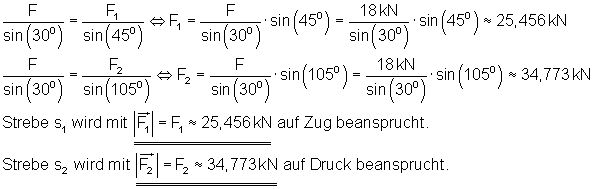
3. Ausführliche Lösung:
Wenn die Resultierende den gleichen Betrag haben soll, wie die beiden, an einem Punkt angreifenden Vektoren, dann muss das Vektordreieck gleichseitig sein. Das bedeutet, die Winkel im Vektordreieck sind alle 600. Der Winkel im Parallelogramm zwischen den beiden Vektoren beträgt dann 1200.
Die an einem Punkt angreifenden gleichgroßen Kräfte haben einen Winkel von 1200 miteinander.
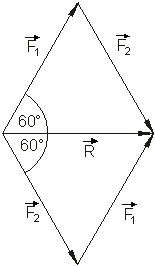
4. Ausführliche Lösung:

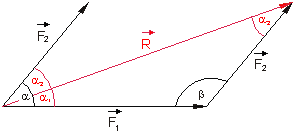
Nach dem Sinussatz gilt:

5. Ausführliche Lösung:
Eine Zeichnung verdeutlicht die Verhältnisse
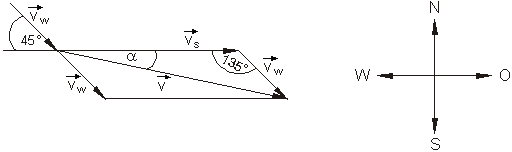
Der Betrag der Eigengeschwindigkeit des Schiffes wird mit vs bezeichnet, die Geschwindigkeit der Wasserströmung mit vw. Die resultierende Geschwindigkeit sei v. Die nebenstehende Windrose zeigt die Himmelsrichtungen auf.
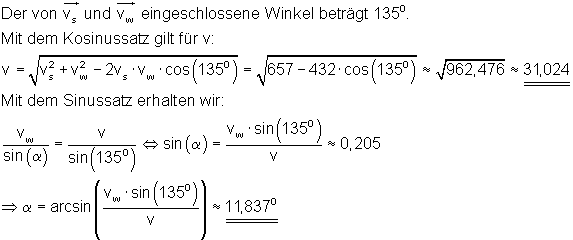
Die Geschwindigkeit des Schiffes über dem Meeresboden beträgt ca. 31,024 Knoten, das sind etwa 57,456 km/h. Eine Kursabweichung in südlicher Richtung von etwa 11,837 Grad ist zu verzeichnen.
6. Ausführliche Lösung:
Eine Zeichnung verdeutlicht die Zusammenhänge
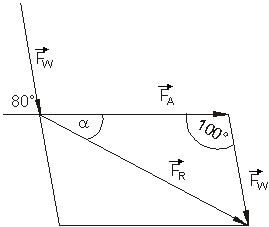
Der Betrag der Antriebskraft des Flugzeugs wird mit FA bezeichnet, die der Windkraft mit FW. Die resultierende Kraft sei FR.
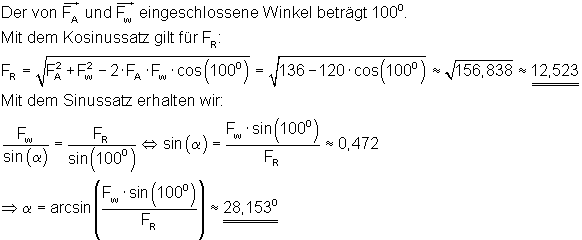
Insgesamt wirkt auf das Flugzeug eine Kraft von 12,523 kN. Um zum Zielort zu gelangen, muss unter einem Winkel von 28,1530 zur eigentlichen Flugroute in Windrichtung Kurs gehalten werden.
Hier findest du die Aufgaben,
die dazugehörige Theorie hier: Rechengesetze für Vektoren in Koordinatendarstellung.
Hier eine Übersicht über alle Beiträge zur Vektorrechnung, darin auch Links zur Theorie und zu weiteren Aufgaben.