Hier findest du die Lösungen der Aufgaben Logarithmen IV berechnen und vereinfachen mit komplettem Lösungsweg.
1. Ausführliche Lösungen
a)
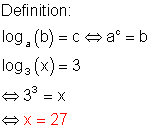
Diese Aufgabe kannst du dir in diesem 📽️ shorts Gleichung mit Logarithmus lösen ansehen.
b)
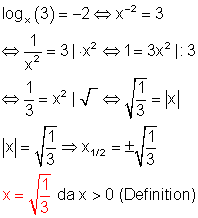
c)
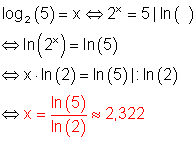
d)
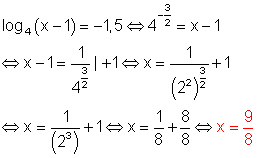
e)
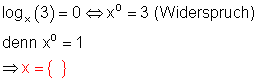
f)
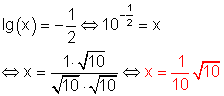
g)
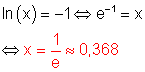
h)
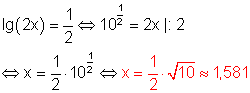
i)
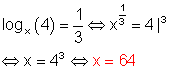
j)
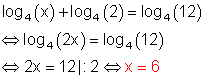
k)
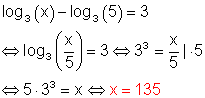
l)
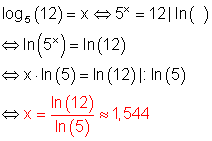
2. Ausführliche Lösungen
a) Multiplikation
![]()
Das kannst du dir auch in diesem 
b) Division
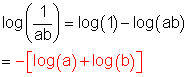
Denn log(1) = 1
Den ersten Teil der Aufgabe kannst du dir auch in diesem 
c)
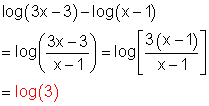
d)
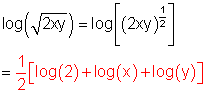
e)
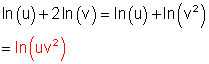
f)
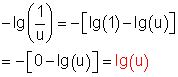
g)
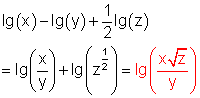
h)
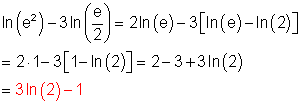
i)
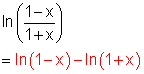
j)
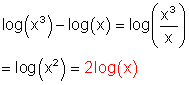
k)
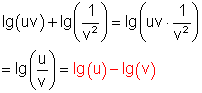
l)
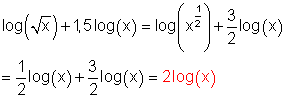
3. Ausführliche Lösungen
a)
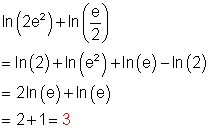
Hier kannst du dir ansehen wie man den
b)
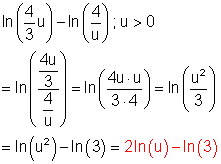
c)
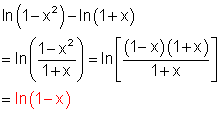
d)
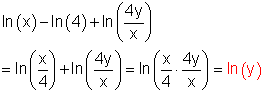
e)
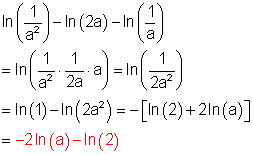
f)
\ln \left(\dfrac{1+x}{2+x}\right) - \ln(x+1)
= \ln \left(\dfrac{1+x}{2+x} \cdot \dfrac{1}{x+1}\right) = \ln \left(\dfrac{1}{2+x}\right)
= \ln(1) - \ln(2+x)
= \color{red}{-\ln(2+x)}
4. Ausführliche Lösungen
a)
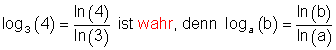
b)
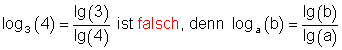
c)
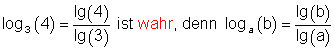
Das 
5. Ausführliche Lösung
![]()
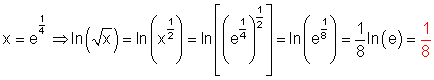
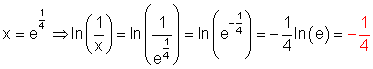
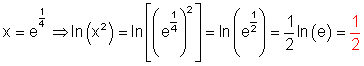
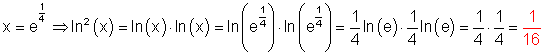
6. Ausführliche Lösung
![]()
![]()
7. Ausführliche Lösung
![]()
![]()
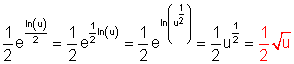
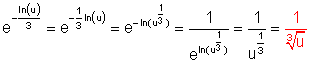
![]()
![]()
![]()
Hier findest du die Aufgaben.
Und hier die dazugehörige Theorie hier: Logarithmen und Logarithmengesetze.
Hier eine Übersicht über weitere Beiträge zu Gleichungen, darin auch Links zur Theorie und zu weiteren Aufgaben.

