Hier findest du die Lösungen der Stochastik Aufgaben vermischt II mit komplettem Lösungsweg.
1.
Eine Urne enthält eine rote, eine schwarze und eine grüne Kugel. Wir ziehen solange eine Kugel ohne Zurücklegen, bis eine grüne Kugel erscheint. Wenn wir im 1. Zug eine grüne Kugel ziehen, ist die Ausspielung 2 €. Aber wenn wir die grüne Kugel im 2. Zug ziehen, so ist die Ausspielung 1 €. Wenn wir die grüne Kugel im 3. Zug ziehen, so ist die Ausspielung 0 €.
Wie hoch muss der Einsatz sein, damit es sich um ein faires Spiel handelt?
Ausführliche Lösung
Mit Hilfe des dreistufigen Baumdiagramms und der Pfadregel errechnet man die Wahrscheinlichkeiten dafür eine grüne Kugel zu ziehen.
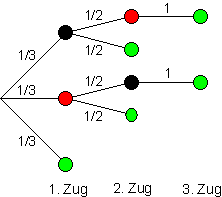

Der Erwartungswert der Ausspielung ist E(X) = 1. Wenn es sich um ein faires Spiel handeln soll, muss der Einsatz 1 € betragen.
2.
Eine Münze wird 5 mal geworfen und p sei 0,5.
a) Bestimme die Wahrscheinlichkeitsverteilung der Zufallsvariablen X: Anzahl der Wappen.
b) Mit welcher Wahrscheinlichkeit wirft man
(1) Höchstens 3 mal Wappen?
(2) Weniger als 3 mal Wappen?
(3) Mindestens 1 mal Wappen?
(4) Mehr als einmal Wappen?
Ausführliche Lösungen
a)
Das Problem kann als 5- stufiger Bernoulli- Versuch betrachtet werden mit n = 5 und p = 0,5. Gesucht ist P(X = k) für k = 0, 1, 2, 3, 4, 5
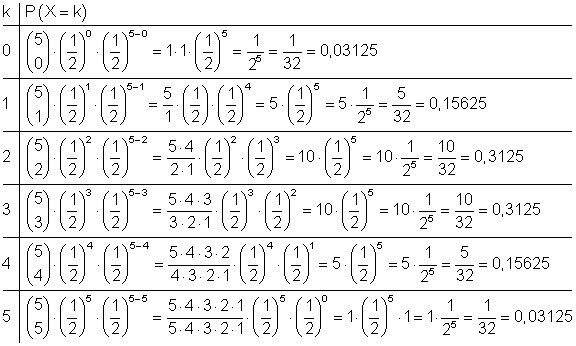
b) (1) Höchstens 3 mal Wappen bedeutet:
![]()
(2) Weniger als 3 mal Wappen bedeutet:
![]()
(3) Mindestens 1 mal Wappen bedeutet:
![]()
(4) Mehr als 1 mal Wappen bedeutet:
3.
Gegeben ist ein n- stufiger Bernoulli- Versuch mit n = 500 und p = 0,33.
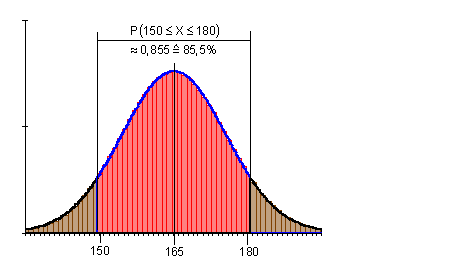
Zu bestimmen ist die Wahrscheinlichkeit für die Anzahl der Erfolge im Intervall [ 150 ; 180]. Es soll mit einer Genauigkeit von drei Stellen hinter dem Komma gerechnet werden.
Ausführliche Lösung
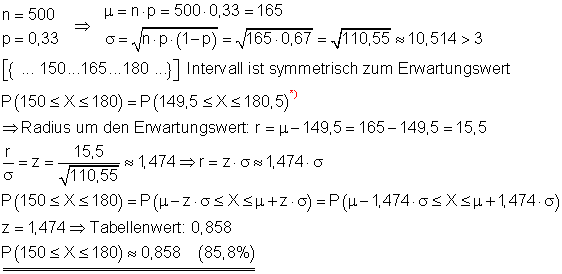
Die Wahrscheinlichkeit für die Anzahl der Erfolge im Intervall [ 150 ; 180 ] beträgt etwa 85,8%.
4.
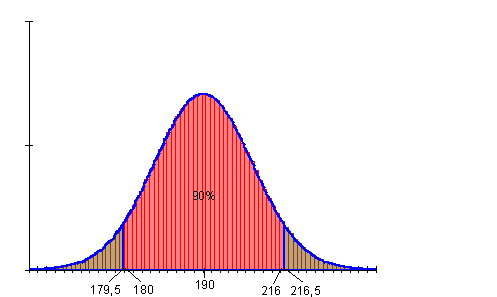
Bestimme die 90%- Umgebung vom Erwartungswert für n = 550 und p = 0,36.
Ausführliche Lösung

Die Wahrscheinlichkeit für die Anzahl der Erfolge im Intervall [ 180 ; 216 ] beträgt etwa 90%.
5.
Gegeben ist ein n- stufiger Bernoulli-Versuch. Gesucht ist die Wahrscheinlichkeit für die Ergebnisse außerhalb von Umgebungen um den Erwartungswert.
a)
![]()
b)
![]()
Ausführliche Lösungen
a)
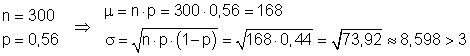
Zu bestimmen ist die Wahrscheinlichkeit für das Intervall [0 ; 161]. Aus der Tabelle kann nur die Wahrscheinlichkeit für ein um den Erwartungswert symmetrisches Intervall abgelesen werden, dieses enthält die Werte [162 …. 168 … 174 ]. Daran anschließend folgt das Intervall [175 …. 300], welches aus Symmetriegründen die gleiche Größe wie [0 ; 161] hat. Es gilt folgender Ansatz:[ { 0 … 161 } {162 … 168 … 174 } { 175 … 300}]
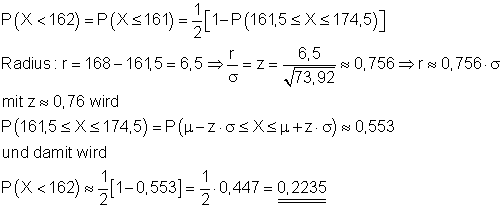
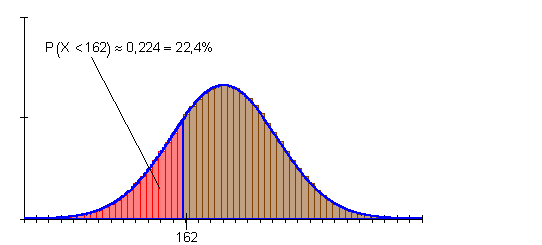
Die Wahrscheinlichkeit für weniger als 162 Erfolge ist etwa 22,4%.
b)
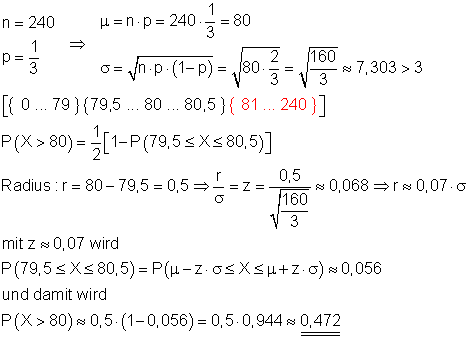
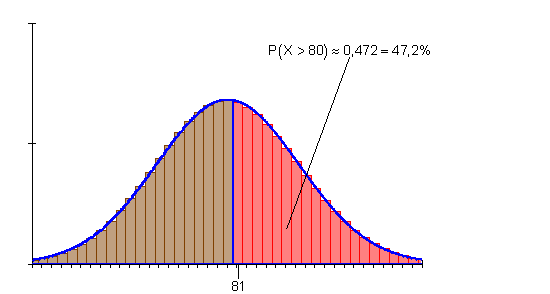
Die Wahrscheinlichkeit für mehr als 80 Erfolge ist etwa 47,2%.
6.
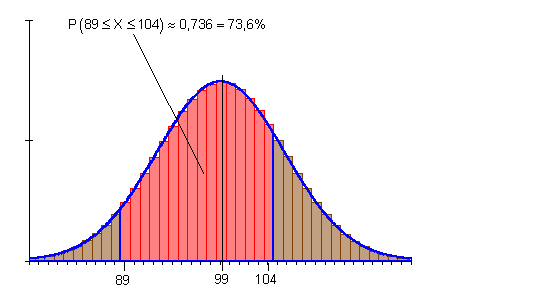
Bestimmen Sie die Wahrscheinlichkeit einer nicht symmetrischen Umgebungvom Erwartungswert. n = 180, p = 0,55, Intervall: [ 89 … 104 ].
Ausführliche Lösung

Die Wahrscheinlichkeit der Erfolge im Intervall [89 ; 104] ist etwa 73,6%.
Hier findest du die Aufgaben.
Und hier eine Übersicht über alle Beiträge zur Wahrscheinlichkeitsrechnung, dort auch Links zu weiteren Aufgaben.