Wenn ihr viele Aufgaben mit den Lösungen zu mehrstufigen Zufallsversuchen in der Wahrscheinlichkeitsrechnung übt, werdet ihr gut in Mathe! Deshalb stelle ich hier noch weitere Aufgaben zur Verfügung.
1.
In einem Gefäß sind 50 gleichartige Kugeln, davon 20 rote und 30 blaue. Es werden 3 Kugeln gezogen mit Zurücklegen. Welche Wahrscheinlichkeit hat das Ereignis?
a) A: Alle Kugeln sind blau.
b) B: Eine Kugel ist blau, zwei sind rot.
c) C: Eine Kugel ist rot, zwei sind blau.
d) D: Höchstens eine Kugel ist rot.
1. Ausführliche Lösungen
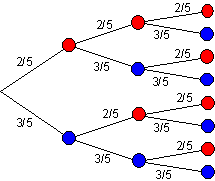
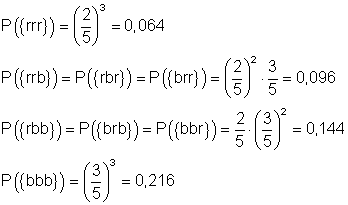
a) A: Alle Kugeln sind blau.
P (A) = P({bbb}) = 0,216
b) B: Eine Kugel ist blau, zwei sind rot.
P (B) = P({rrb}) + P({rbr}) + P({brr}) = 3 ·0,096 = 0,288
c) C: Eine Kugel ist rot, zwei sind blau.
P(C) = P({rbb}) + P({brb}) + P({bbr}) = 3 · 0,144 = 0,432
d) D: Höchstens eine Kugel ist rot. Das bedeutet keine oder nur eine.
P(D) = P({bbb}) + P({bbr}) + P({brb}) + P({rbb}) = 0,216 + 3 · 0,144 = 0,648
2.
In einem Gefäß sind 50 gleichartige Kugeln, davon 20 rote und 30 blaue. Es werden 3 Kugeln gezogen ohne Zurücklegen. Welche Wahrscheinlichkeit hat das Ereignis?
a) A: Alle Kugeln sind blau.
b) B: Eine Kugel ist blau, zwei sind rot.
c) C: Eine Kugel ist rot, zwei sind blau.
d) D: Höchstens eine Kugel ist rot.
2. Ausführliche Lösungen
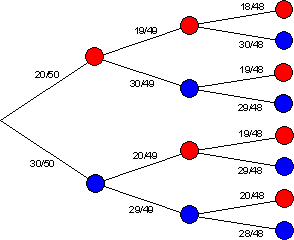

a) A: Alle Kugeln sind blau.
![]()
b) B: Eine Kugel ist blau, zwei sind rot.
![]()
c) C: Eine Kugel ist rot, zwei sind blau.
![]()
d) D: Höchstens eine Kugel ist rot. Das bedeutet keine oder nur eine.
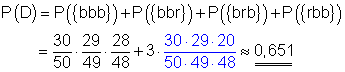
3.
Bei der Produktion von Tongefäßen hat man erfahrungsgemäß 20% Ausschuss.
a) Wie groß ist die Wahrscheinlichkeit das bei der Herstellung von vier Gefäßen genau drei brauchbar sind?
b) Wie groß ist die Wahrscheinlichkeit das bei der Herstellung von vier Gefäßen genau zwei brauchbar sind?
c) Wie groß ist die Wahrscheinlichkeit das bei der Herstellung von vier Gefäßen mindestens drei brauchbar sind?
3. Ausführliche Lösungen
Modell:
Urne mit einer roten (Ausschuss) und vier grünen (kein Ausschuss) Kugeln. Viermal Ziehen mit Zurücklegen.
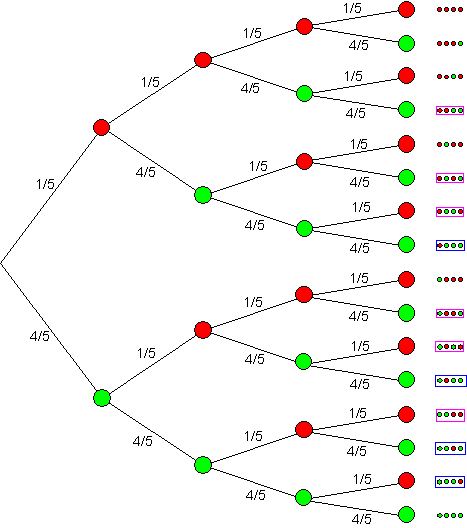
a) A: Drei von vier sind brauchbar. Das Baumdiagramm enthält 4 Pfade, die für das Ereignis A relevant sind.
![]()
b) B: Zwei von vier sind brauchbar. Das Baumdiagramm enthält 6 Pfade, die für das Ereignis B relevant sind.
![]()
c) C: Mindestens drei von vier sind brauchbar. Das bedeutet drei oder mehr sind brauchbar.
![]()
4.
Im Lager einer Töpferei befinden sich 100 frisch gefertigte Tontöpfe. Man weiß, das 20% davon fehlerhaft sind. Vier Tontöpfe werden zufällig entnommen.
a) Wie groß ist die Wahrscheinlichkeit das die vier entnommenen Töpfe fehlerfrei sind?
b) Wie groß ist die Wahrscheinlichkeit das von den vier entnommenen Töpfen drei fehlerfrei sind?
c) Wie groß ist die Wahrscheinlichkeit das von den vier entnommenen Töpfen mindestens drei fehlerfrei sind?
4. Ausführliche Lösungen
Modell:
Urne mit 20 roten (fehlerhaft) und 80 grünen (fehlerfrei) Kugeln. Viermal Ziehen ohne Zurücklegen.
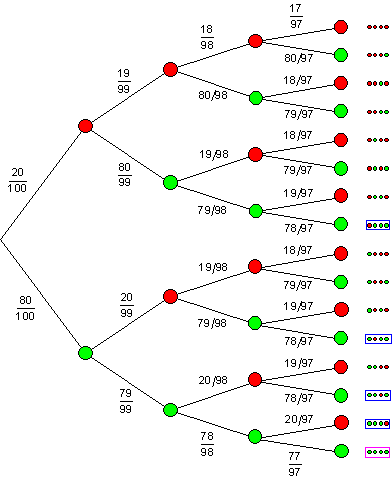
a) A: Alle 4 Töpfe sind fehlerfrei. Das Baumdiagramm enthält einen Pfad, für den das Ereignis A zutrifft.
![]()
b) B: Drei der vier entnommenen Töpfe sind fehlerfrei. Das Baumdiagramm enthält 4 Pfade, die für das Ereignis B relevant sind.
![]()
c) C: Mindestens drei der vier entnommenen Töpfe sind fehlerfrei. Das bedeutet drei oder mehr sind fehlerfrei.
![]()
5.
Bei einer Produktionskontrolle wird ein bestimmter Fehler in 10% der Fälle übersehen. Deshalb wird das Produkt von drei verschiedenen Personen kontrolliert. Bestimme die Wahrscheinlichkeit dafür, dass ein unbrauchbares Produkt.
a) Spätestens bei der 2. Kontrolle als unbrauchbar erkannt wird.
b) Erst bei der 3. Kontrolle als unbrauchbar erkannt wird.
c) Nicht als unbrauchbar erkannt wird.
5. Ausführliche Lösungen
Modell:
Urne mit 1 roten (fehlerhaft) und 9 grünen (fehlerfrei) Kugeln. Dreimal Ziehen mit Zurücklegen.
Begründung für mit Zurücklegen:
Die Kontrollen geschehen unabhängig voneinander. Die Ausgangssituation vor jeder Kontrolle ist immer wieder die gleiche.(Übersehen des Fehlers 10%).
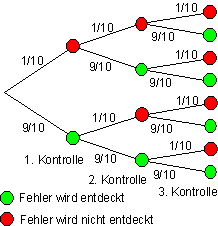
a) A: Spätestens bei der 2. Kontrolle erkannt bedeutet, der Fehler wird in der ersten oder in der zweiten Kontrolle erkannt.
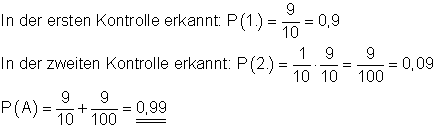
b) B: Erst bei der 3. Kontrolle erkannt.
![]()
c) C: Wird nicht erkannt.
![]()
6.
In einer Fabrik wird Porzellangeschirr hergestellt. Jedes Teil wird nacheinander in verschiedenen Kontrollgängen auf Form, Farbe und Oberflächenbeschaffenheit geprüft. Erfahrungsgemäß muss bei 25% die Form beanstandet werden. Die Farbkontrolle passieren 85% der Teile ohne Beanstandung. In 20% aller Fälle genügt die Oberfläche nicht den Ansprüchen der 1. Wahl. Nur wenn alle drei Kontrollen ohne Beanstandung durchlaufen sind, kann ein Teil als 1. Wahl verkauft werden. Ein Teil ist 2. Wahl, wenn die Qualität an nur einer Kontrollstelle nicht ausreicht. Alle übrigen Porzellanteile gelten als Ausschussware.
a) Stelle die dreifache Kontrolle in einem Baumdiagramm dar.
b) Wie groß ist die Wahrscheinlichkeit dafür, dass ein Teil 1. Wahl ist?
c) Wie groß ist die Wahrscheinlichkeit dafür, dass ein Teil 2. Wahl ist?
d) Wie groß ist die Wahrscheinlichkeit dafür, dass ein Teil Ausschuss ist?
6. Ausführliche Lösungen
a)
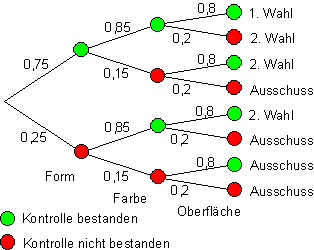

b) P(1. Wahl) = 0,51
c) P(2. Wahl) = 0,1275 + 0,09 + 0,17 = 0,3875
d) P(Ausschuss) = 0,0225 + 0,0425 + 0,03 + 0,0075 = 0,1025
7.
In der Lotterie A gibt es von 10000 Losen 4500 Gewinne. In der Lotterie B sind unter 15000 Losen 9500 Gewinne. Jemand kauft von jeder Lotterie ein Los.
a) Wie groß ist die Wahrscheinlichkeit, in beiden Lotterien gleichzeitig zu gewinnen?
E1: Gewinn in beiden Lotterien.
b) Wie groß ist die Wahrscheinlichkeit nichts zu gewinnen?
E2: Gewinn in keiner Lotterie?
c) Wie groß ist die Wahrscheinlichkeit, in mindestens einer Lotterie zu gewinnen?
E3: Gewinn in mindestens einer Lotterie.
7. Ausführliche Lösungen
a)
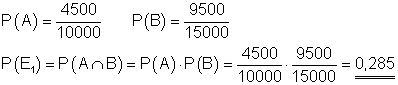
b) Es liegt kein Gewinn vor, wenn man in Lotterie A und in Lotterie B nichts gewinnt.
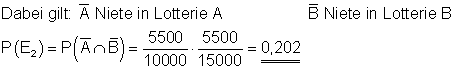
c)
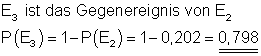
Hier findest du die Aufgaben hierzu.
Und hier die Theorie hierzu.
Hier findest du eine Übersicht über alle Beiträge zum Thema Wahrscheinlichkeitsrechnung, darin auch Links zu Aufgaben.

