Im letzten Beitrag haben wir uns mit einstufigen Ereignissen beschäftigt. Zum Beispiel wenn wir einen Würfel nur einmal werfen. Jetzt geht es um mehrstufige Zufallsversuche. Dazu stelle ich viele Beispiele vor. Außerdem erkläre ich die 1. und 2. Pfadregel. Schließlich geht es um das Laplace-Experiment. Am Schluss verlinke ich zu Aufgaben.
Durch Klick auf einen Link kommt ihr sofort zum jeweiligen Thema:
- Beispiel einstufig und mehrstufige Zufallsversuche mit Münzen
- Beispiel mehrstufiger Zufallsversuch ohne zurücklegen
- Pfadregeln
- Beispiel mehrstufiger Zufallsversuch mit zurücklegen
- Beispiel mehrstufiger Zufallsversuch ohne zurücklegen
Häufig werden Zufallsversuche untersucht, die aus mehr als einem einzigen Experiment bestehen. Diese Versuche setzen sich aus mehreren hintereinander ausgeführten einstufigen Versuchen zusammen. Mit anderen Worten: mehrstufige Zufallsereignisse.
Beispiel einstufig und mehrstufige Zufallsversuche mit Münzen:
Wir werfen zwei Münzen gleichzeitig. Das ist also ein einstufiges Ereignis. Anschließend kann man bei jeder Münze entweder w = Wappen oder z = Zahl sehen. Die Ergebnismenge setzt sich also so zusammen:
S = { ww ; wz ; zw ; zz }.
Es gibt 4 Möglichkeiten. Wie wir im letzten Beitrag gesehen haben, ist die Wahrscheinlichkeit für jede Kombination dabei gleich groß. Es handelt sich also um ein Laplace-Experiment.
P(ww) = P(wz) = P(zw) = P(zz) = 0,25.
Danach werfen wir eine Münze zweimal hintereinander. Das sieht erst einmal genauso aus. Aber später unterscheiden wir ob wir die Münze zurücklegen oder nicht. Deshalb gehen wir jetzt anders vor.
Beim ersten Wurf können wir entweder w oder z sehen. Die Wahrscheinlichkeit beträgt also 0,5. Deshalb schreiben wir dies in den ersten Ast eines Baumdiagramm.
Der zweite Wurf kann wieder w oder z ergeben. Also schreiben ebenfalls 0,5 an den nächsten Zweig.
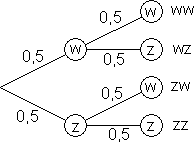
Die Ergebnismenge S = { ww ; wz ; zw ; zz } ist dieselbe wie im ersten Versuch.
Die Wahrscheinlichkeit für jedes einzelne Ergebnis erhalten wir, indem wir die Wahrscheinlichkeiten längs des Pfades multiplizieren:
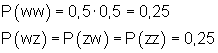
Wir erhalten also die gleichen Wahrscheinlichkeiten wie oben. Soweit so schön.
Mit Hilfe solcher Ergebnisbäume kann man übersichtlich Wahrscheinlichkeiten bei mehrstufigen Zufallsversuchen berechnen. Dabei stellt jeder Pfad ein Ergebnis des Zufallsexperimentes dar.
Beispiel mehrstufiger Zufallsversuch ohne zurücklegen:
Schauen wir uns zuerst ein Beispiel eines mehrstufigen Zufallsversuchs ohne zurücklegen an:
Der Schülerrat eines Berufskollegs besteht aus 3 Schülern und 2 Schülerinnen. Es wird ausgelost, wer in diesem Jahr Vorsitzender und Stellvertreter wird. Zuerst wird der Vorsitzende und dann der Stellvertreter ausgelost.
a) Mit welcher Wahrscheinlichkeit wird je eine Schülerin Vorsitzende und eine Schülerin Stellvertreterin?
b) Mit welcher Wahrscheinlichkeit wird eine Schülerin Vorsitzende und ein Schüler Stellvertreter?
c) Mit welcher Wahrscheinlichkeit wird eine Schülerin Stellvertreterin?
Es handelt sich dabei um ein zweistufiges Zufallsexperiment. Dies simuliert man gerne mit einem sogenannten Urnenmodell. Wir stellen uns dabei vor, in der Urne befinden sich 5 Kugeln. 2 rote stehen für Schülerin und 3 schwarze stehen für Schüler. Also zwei r und drei s. Deshalb steht links im Baumdiagramm rrsss.
Wir ziehen nacheinander zwei Kugeln aus der Urne. Das nennt man auch ‚Ziehen ohne zurücklegen‘.
Für Aufgabe a) schauen wir uns den obersten Zweig an: Es gibt 2 rote Kugeln und insgesamt 5 Kugeln. Folglich beträgt die Wahrscheinlichkeit, eine rote Kugel zu ziehen 2/5. Deshalb schreiben wir diese Zahl an den Zweig. Danach bleiben in der Urne eine rote und drei schwarze in der Urne. Denn eine Schülerin ist Vorsitzende. Deshalb steht oberhalb der ersten roten Kugel rsss.
Es gibt jetzt 1 rote Kugeln und insgesamt 4 Kugeln. Folglich beträgt die Wahrscheinlichkeit, eine rote Kugel zu ziehen nur noch 1/4. Deshalb schreiben wir diese Zahl an den Zweig.
Die Wahrscheinlichkeit, zwei rote Kugeln zu ziehen berechnet man, indem man die beiden Wahrscheinlichkeiten multipliziert. Also ist P(rr) = 0,1.
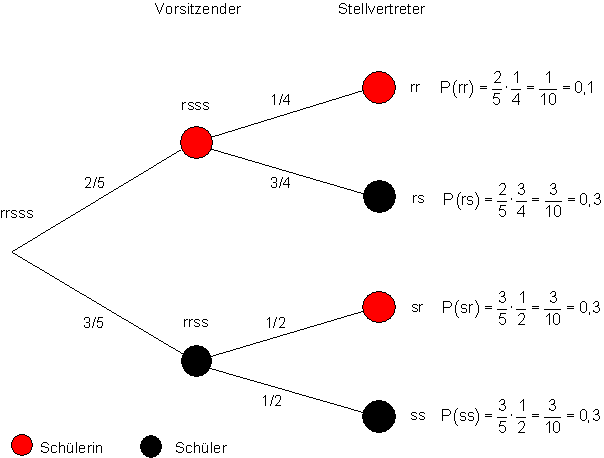
a)
A: Eine Schülerin ist Vorsitzende, die andere Stellvertreterin.
P(A) = P(rr) = 0,1.
Was rechts steht, nennt man Ergebnis. Genauso geht man für alle anderen Ergebnisse vor. Also auch für Aufgabe b). Diese finden wir im zweiten Zweig:
b)
B: Schülerin ist Vorsitzende und Schüler ist Stellvertreter.
P(B) = P(rs) = 0,3.
Die Lösung für Aufgabe c) ist aufwendiger. Denn eine Schülerin kann Stellvertreterin werden, wenn ein Schüler Vorsitzender ist und wenn eine Schülerin Vorsitzender ist. Im Baumdiagramm sehen wir deshalb im ersten und dritten Zweig eine rote Kugel. Also müssen wir diese beiden Wahrscheinlichkeiten addieren. Das nennt man ein Ereignis:
c)
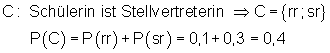
Pfadregeln
Wir müssen also überlegen, ob wir nach einem Ergebnis fragen, das am Ende eines Zweiges steht. Dann trifft die erste Pfadregel zu:
1. Pfadregel:
In einem Baumdiagramm ist die Wahrscheinlichkeit eines Ergebnisses gleich dem Produkt der Wahrscheinlichkeiten entlang des zugehörigen Pfades.
2. Pfadregel
Fragen wir jedoch nach einem Ereignis, das am Ende mehrerer Zweige steht:
In einem Baumdiagramm ist die Wahrscheinlichkeit eines Ereignisses gleich der Summe der für dieses Ereignis zugehörigen Pfadwahrscheinlichkeiten.
Wir müssen also erst die Wahrscheinlichkeiten für ein einzelnes Ergebnis berechnen. Danach können wir für ein Ereignis sehen, welche wir addieren müssen.
Bevor man Wahrscheinlichkeiten berechnet, sollte man zuerst genau überlegen. Erst ganz am Schluß rechnen.
Wahrscheinlichkeitsverteilung:
In einem Baumdiagramm führt jeder Pfad zu einem Ergebnis des Zufallsversuches. Wenn man die Wahrscheinlichkeiten der einzelnen Pfade in einer Tabelle zusammenfasst, erhält man die Wahrscheinlichkeitsverteilung:
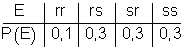
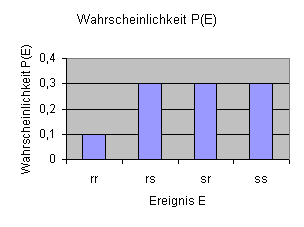
Sie lässt sich auch graphisch in einem Säulendiagramm darstellen.
Die Summe der Wahrscheinlichkeiten ergibt immer 1.
Beispiel mehrstufiger Zufallsversuch mit zurücklegen:
Schauen wir mal, was hier anders ist:
In einer Urne befinden sich 3 rote und 2 gelbe Kugeln. Nacheinander werden zwei Kugeln mit zurücklegen gezogen.
a) Erstelle das Baumdiagramm! Und dann die Wahrscheinlichkeitsverteilung als Tabelle und als Diagramm.
b) Berechne die Wahrscheinlichkeit für das Ereignis
A: Die gezogenen Kugeln haben ungleiche Farben.
c) Berechne die Wahrscheinlichkeit für das Ereignis
B: Mindestens eine gezogenen Kugel ist gelb.
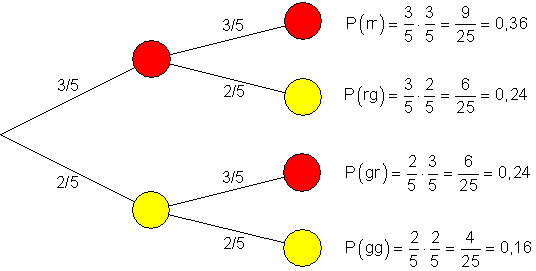
Weil wir die Kugeln zurücklegen, beträgt die Wahrscheinlichkeit, eine rote zu ziehen, immer 3/5. Eine gelbe zu ziehen dagegen 2/5. Ansonsten rechnen wir wie oben.
a) Baumdiagramm
Wahrscheinlichkeitsverteilung als Tabelle:
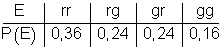
Wahrscheinlichkeitsverteilung als Diagramm
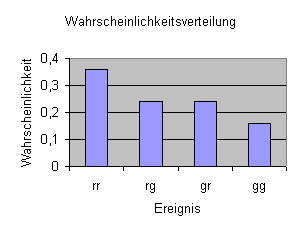
b)
Ungleiche Farben haben die Ergebnisse rg und gr. Deshalb addieren wir dies beiden Wahrscheinlichkeiten:
![]()
c)
Eine gelbe Kugel sehen wir bei rg, gr und gg. Also addieren wir deren Wahrscheinlichkeiten:
![]()
Beispiel mehrstufiger Zufallsversuch ohne zurücklegen:
Versuche nun einmal selber diese Aufgaben zu lösen!
In einer Urne befinden sich 3 rote und 4 gelbe Kugeln. Nacheinander werden zwei Kugeln ohne zurücklegen gezogen.
a) Erstelle das Baumdiagramm. Und dann die Wahrscheinlichkeitsverteilung als Tabelle und als Diagramm.
b) Berechne die Wahrscheinlichkeit für das Ereignis A: Die zweite gezogene Kugel ist rot.
c) Berechne die Wahrscheinlichkeit für das Ereignis B: Beide Kugeln haben die gleiche Farbe.
a)
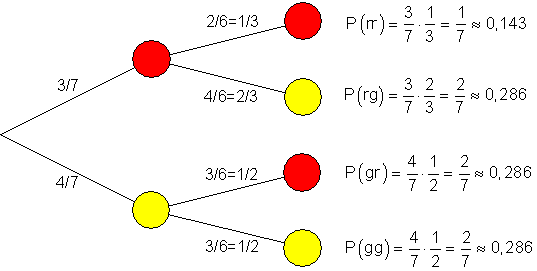
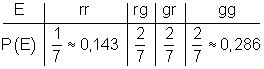
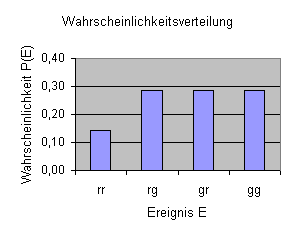
b)
![]()
c)
![]()
Außerdem Aufgaben zu Mehrstufige Zufallsversuche II.
Im nächsten Beitrag: Das Urnenmodell vertiefen wir dieses Thema.
Hier findest du eine Übersicht über alle Beiträge zum Thema Wahrscheinlichkeitsrechnung. Darin auch Links zu Aufgaben.
Dazu kannst du auch den Wikipedia-Artikel zur Wahrscheinlichkeitstheorie lesen.


