In diesem Beitrag stelle ich viele Beispiele für das Urnenmodell vor.
Das Ziehen kann man auf zwei verschiedene Arten durchführen: Wir ziehen eine Kugel und legen sie danach wieder zurück.
Das entspricht dem Urnenmodell mit Zurücklegen in der Wahrscheinlichkeitsrechnung.
Wenn wir die Kugel nach dem Ziehen nicht wieder zurücklegen, sprechen wir vom Urnenmodell ohne Zurücklegen.
Im letzten Beitrag haben wir uns bereits mit mehrstufigen Zufallsversuchen beschäftigt.
Viele Zufallsexperimente können auf das Urnenmodell zurückgeführt werden. Z. B. das „Dreimalige Münzwerfen“ kann man auch mit einer Urne mit 2 verschiedenen Kugeln beschreiben. Dann zieht man dreimal jeweils eine Kugel und legt sie wieder zurück.
Zufallsversuche mit Urnenmodell
Vielen fällt es schwer, zu einer Textaufgabe ein Urnenmodell zu erstellen. Deshalb erkläre ich dies anhand einiger Beispiele. Hier habe ich Tipps zum Lösen von Aufgaben von mehrstufigen Zufallsversuchen gegeben.
Beispiel zweimal 6 würfeln
Wie groß ist die Wahrscheinlichkeit bei zweimaligem würfeln jeweils eine 6 zu werfen?
Zweimal würfeln, also zweimal ziehen mit Zurücklegen.
Statt des Würfels können wir auch eine Urne mit 6 Kugeln nummeriert von 1 bis 6 nehmen.
Jedesmal beträgt die Wahrscheinlichkeit, eine 6 zu würfeln, 1/6.
Beim zweimal Würfeln ist die gesuchte Wahrscheinlichkeit also
![]()
Beispiel: 10 von 25 Schüler ohne Hausausgaben
In einer Klasse mit 25 Schülern haben 10 Schüler die Hausaufgaben nicht gemacht. Dann kontrolliert der Lehrer zufällig einen Schüler. Mit welcher Wahrscheinlichkeit erwischt er jemanden, der die Hausaufgaben nicht gemacht hat?
Der Lehrer kontrolliert einen Schüler, also einmal Ziehen.
Statt der Schüler können wir diesmal eine Urne mit 25 Kugeln nehmen. Davon sind 15 weiß und 10 schwarz.
Die gesuchte Wahrscheinlichkeit ist also:
![]()
Beispiel 2 Schüler auslosen
Von den 120 Schüler/innen einer Oberstufe sind 15% männlich. Zwei Schüler/innen davon werden für die Teilnahme an einem Wettbewerb ausgelost. Wie groß ist die Wahrscheinlichkeit, dass es zwei Jungs sind?
Zwei werden ausgelost, also zweimal Ziehen ohne Zurückziehen.
15% von 120 Schüler/innen sind 18. Wir stellen uns eine Urne mit 120 Kugeln vor. Davon sind 102 weiße Kugeln (für weiblich) und 18 schwarze Kugeln (für männlich).
Beim ersten Ziehen ist die Wahrscheinlichkeit, einen Jungen zu ziehen 18 von 120. Danach ist ja ein Junge weniger da. Deshalb beträgt die Wahrscheinlichkeit beim zweiten Ziehen 17 von 119. Die gesuchte Wahrscheinlichkeit beträgt also:
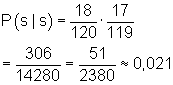 .
.
Beispiel: Mutter und zwei Söhne
Bei 53% aller Geburten ist das Baby männlich. Wie groß ist die Wahrscheinlichkeit, dass eine Mutter aufeinanderfolgend 2 Söhne zur Welt bringt?
Eine Mutter bringt immer mit der gleichen Wahrscheinlichkeit Kinder zur Welt. Anders formuliert: nach jeder Geburt herrscht wieder die gleiche Ausgangssituation. Deshalb entspricht dies zweimal ziehen mit Zurücklegen. Wir wählen also eine Urne mit 100 Kugeln. Davon sind 53 blau für Söhne und 47 rosa für Töchter.
Die gesuchte Wahrscheinlichkeit beträgt demnach:
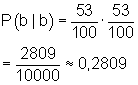
Eine andere Situation herrscht, wenn man von z.B. von 100 neugeborenen Kindern ausgeht, von denen 53% Jungen sind. Wenn man zufällig 2 Kinder auswählt, entspräche dies dem Ziehen ohne Zurücklegen. Dafür beträgt die Wahrscheinlichkeit:
![]()
Beispiel Tongefäße:
Bei der Herstellung von Tongefäßen geht man davon aus, dass 20% Ausschuss sind. Wie groß ist die Wahrscheinlichkeit, dass bei der Herstellung von 3 Gefäßen genau 2 brauchbar sind?
Urnenmodell:
Statt 80 grüne Kugeln für die brauchbaren und 20 rote für den Ausschuss, können wir auch 8 und 2 Kugeln nehmen. Die Wahrscheinlichkeit für eine Grüne beträgt 0,8, für eine Rote 0,2.
Dann ziehen wir dreimal mit Zurücklegen. Dabei darf die erste, die zweite oder die dritte unbrauchbar sein. Deshalb berechnen wir die Wahrscheinlichkeit für eine davon und multiplizieren dies mit 3.

Beispiel genau zwei hintereinander
Aus vier Personen Angela (A), Balduin (B), Christin (C), Dogan (D) lost man zwei zum Geschirrspülen aus. Wobei eine Person abspült und eine abtrocknet. Mit welcher Wahrscheinlichkeit erwischt es zuerst Christin und dann Balduin?
Urnenmodell:
Wir nehmen eine Urne mit 4 Kugeln mit der Aufschrift A, B, C und D. Hier kommt es auf die Reihenfolge der gezogenen Kugeln an. Es werden zwei Personen ausgelost, also zweimal Ziehen ohne zurücklegen. Beim ersten Losen besteht für Christin die Wahrscheinlichkeit 1/4. Es sind dann nur noch drei Personen übrig, also besteht für Balduin die Wahrscheinlichkeit 1/3. Das ist ein Zweig im Baumdiagramm, deshalb müssen wir beides multiplizieren.

Beispiel Fahrzeuge:
Bei einer Verkehrszählung sind 65% der vorbeifahrenden Fahrzeuge Pkw, 30% Lkw und 5% sonstige Fahrzeuge. Wie groß ist die Wahrscheinlichkeit, dass unter drei vorbeifahrenden Fahrzeugen das erste ein Pkw, das zweite ein Lkw und das dritte ein sonstiges Fahrzeug ist?
Urnenmodell:
Wir nehmen eine Urne mit 100 Kugeln. Davon 65 rote für Pkws, 30 schwarze für Lkws und 5 weiße für sonstiges Fahrzeug. Dann ziehen wir dreimal mit Zurücklegen. Deshalb müssen wir alle drei Wahrscheinlichkeiten multiplizieren:
![]()
Beispiel 3 mal mindestens:
Wie oft muss ein Spieler einen Würfel mindestens werfen, damit er mit einer Wahrscheinlichkeit von mindestens 90% mindestens eine 6 wirft.
Urnenmodell:
Vorgehen bei 3-mal-mindestens-Aufgaben:
Aufgaben mit dreimal „mindestens“ müssen wir wie folgt lösen:
Es ist viel einfacher, danach zu fragen, wie groß die Wahrscheinlichkeit bei n Versuchen ist, keine 6 zu würfeln. Das ist nämlich das Gegenteil von mindestens eine 6 zu würfeln. Also \bar A . Die Wahrscheinlichkeit für unser gesuchtes Ereignis ist dann 1 - \bar A .
In unserem Beispiel nehmen wir eine Urne mit 6 Kugeln, eine davon grün. Die Wahrscheinlichkeit, eine 6 zu würfeln, beträgt 1/6, also 0,1666, also 16,66 %. Die Wahrscheinlichkeit, keine 6 zu würfeln ist 5/6.
Wir ziehen n-mal mit Zurücklegen. Dabei ist die Zahl n unbekannt.
Wir definieren dazu die Ereignisse:
Ereignis A: eine 6 werfen.
Das Gegenereignis \bar A dagegen: keine 6 werfen.
Bei n Würfen beträgt die Wahrscheinlichkeit dafür:
– in jedem Wurf eine 6 zu werfen:
\frac{1}{6} \cdot \frac{1}{6} \cdot ... \cdot \frac{1}{6} Das n mal, deshalb: = (\frac{1}{6})^n
– in jemden Wurf keine 6 zu werfen:
\frac{5}{6} \cdot \frac{5}{6} \cdot ... \cdot \frac{5}{6} = (\frac{5}{6})^n
Schließlich definieren das Ereignis E: Bei n Würfen insgesamt mindestens eine 6 werfen.
Das Gegenereignis lautet \bar E : Bei n Würfen insgesamt keine 6 werfen.
Die Wahrscheinlichkeit von \bar E ist bereits bekannt: P( \bar E) = (\frac{5}{6})^n .
Damit ist die Wahrscheinlichkeit von E: P(E) = 1 - P( \bar E) = 1 - (\frac{5}{6})^n .
In der Aufgabenstellung ist gefordert, dass P(E) ≥ 0,90 sein soll.
Wir suchen also in 1 - (\frac{5}{6})^n ≥ 0,90 die Zahl n für die Anzahl der Würfe.
Dazu formen wir um:
1 - (\frac{5}{6})^n ≥ 0,90 | - 1
\Leftrightarrow - (\frac{5}{6})^n ≥ - 0,1 | \cdot (-1)
\Leftrightarrow (\frac{5}{6})^n ≤ 0,1 | ln
Jetzt müssen wir logarithmieren:
\Leftrightarrow n \cdot ln (\frac{5}{6}) ≤ ln (0,1) | : ln (\frac{5}{6}) \\ \approx -0,18 < 0 \\ \Rightarrow Relationszeichen ≤ umdrehen
\Leftrightarrow n \color{red}{≥} \color{black} {\dfrac{ln(0,1)} {ln(\frac{5}{6})} \approx 12,629}
Zur Kontrolle rechnen wir: 1 - (\frac{5}{6})^{13} = 0,9065
Man muss den Würfel also mindestens 13 mal werfen um mit einer Sicherheit von mindestens 90% mindestens einmal die 6 zu erhalten. Anders ausgedrückt: Ich darf höchstens in 10 von 100 Fällen bei 12 mal würfeln keine 6 bekommen.
Aufgaben hierzu.
Außerdem Aufgaben zu Mehrstufige Zufallsversuche II.
Bislang wurden nur Wahrscheinlichkeiten einzelner Ereignisse berechnet. Ereignisse können aber auch verknüpft werden. Damit beschäftigen wir uns im nächsten Beitrag Wahrscheinlichkeit bei verknüpften Ereignissen.
Hier findest du eine Übersicht über alle Beiträge zum Thema Wahrscheinlichkeitsrechnung. Darin auch Links zu Aufgaben.


