Hier geht es um Wahrscheinlichkeiten, die man mit ‚und‘ und ‚oder‘ verknüpft. Dazu stelle ich viele Beispiele und Übungen zur Verfügung. Außerdem kannst du dir ein Video dazu ansehen.
Beispiel Und Oder Wahrscheinlichkeit:
Dazu kannst du dir das 📽️ Video verknüpfte Wahrscheinlichkeiten ansehen.
In einem Abiturjahrgang am Berufskolleg sind 100 Schüler/innen. Davon lernen 87 Spanisch (S) und 75 Französisch (F), 70 beherrschen beide Fremdsprachen.
a) Wie viele Schüler/innen lernen Französisch oder Spanisch? Oder bedeutet hierbei Französisch, Spanisch oder beides.
b) Wir wählen eine Schüler/in zufällig aus. Berechne die Wahrscheinlichkeit dafür, dass er/sie Spanisch oder Französisch gelernt hat. Oder bedeutet dabei Französisch, Spanisch oder beides.
Lösung:
a) Man kann nun nicht einfach die Zahlen für Spanisch und Französisch addieren, denn dann käme man auf eine Schülerzahl von 87 + 75 = 162.
Das ist falsch, weil man die Schüler/innen die Spanisch und Französisch gelernt haben, damit doppelt zählt. 87 Schüler/innen mit Spanisch, davon 70 mit Spanisch und Französisch. Also 17 nur mit Spanisch. 75 Schüler/innen mit Französisch, davon 70 mit Spanisch und Französisch, also 5 nur mit Französisch.
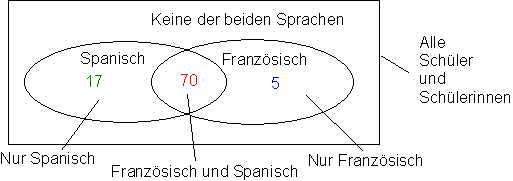
Die 70 Schüler/innen mit Spanisch und Französisch sind sowohl in den 87 mit Spanisch als auch in den 75 mit Französisch enthalten. Mit anderen Worten, die 70 Schüler/innen stellen die Und-Verbindung von Spanisch und Französisch dar.
Addiert man die Anzahl der Schüler/innen mit Spanisch (87) und die Anzahl der Schüler/innen mit Französisch (75), so hat man die Anzahl der Schüler/innen mit Spanisch und Französisch doppelt gezählt. Daher muss man 70 von der Summe (162) subtrahieren.
Anzahl der Schüler/innen mit Spanisch oder Französisch sind also:
87 + 75 – 70 = 92
Das heißt, 8 Schüler/innen lernen in der Oberstufe keine der beiden Fremdsprachen.
b) Zuerst definieren wir die Ereignisse:
S: Schüler/in lernt Spanisch. F: Schüler/in lernt Französisch.
Wahrscheinlichkeit P(S oder F) = \dfrac {87+75-70}{100} = 0,92
Wenn wir den Term umformen:
P(S oder F) = \dfrac {87}{100} + \dfrac{75}{100} - \dfrac{70}{100} = 0,87 + 0,75 – 0,70 = 0,92
. P(S) P(F) P(S und F)
Dies ist die Summenregel, mit anderen Worten: Additionsregel.
Summenregel = Additionsregel
Setzt sich ein Ereignis E aus den Ereignissen A und B zusammen, die sich überschneiden können, dann darf man diese gemeinsamen Ereignisse nicht doppelt berücksichtigen. D. h. eine oder-Verknüpfung kann gemeinsame Ergebnisse enthalten.
Sind A und B Ereignisse und gilt E = A ∪ B (Oder-Ereignis);
dann ist die Wahrscheinlichkeit für das Ereignis E
P(E) = P(A ∪ B) = P(A) + P(B) – P(A ∩ B).
In unserem Beispiel: P(E) = P(S ∪ F) = P(S) + P(F) – P( S∩F)
Anders ausgedrückt: Die Wahrscheinlichkeit eines Oder-Ereignisses ist die Summe der Wahrscheinlichkeiten der beiden Ereignisse, vermindert um die Wahrscheinlichkeit des Und-Ereignisses.
Dazu kannst du dir das 📽️ Video verknüpfte Wahrscheinlichkeiten ansehen.
Beispiel Oder Wahrscheinlichkeit:
Wir werfen einen Würfel einmal. Danach legen wir zwei Ereignisse fest.
A: Die Augenzahl ist größer als 3.
B: Die Augenzahl ist eine gerade Zahl.
Dann legen wir ein neues Ereignis fest:
C: Die Augenzahl ist größer als 3 oder die Augenzahl ist eine gerade Zahl.
Das Ereignis C ist eine Oder-Verknüpfung aus A und B. Bestimme die Wahrscheinlichkeit für die Oder-Verknüpfung P (C).
Zuerst bilden wir die Ergebnismengen von A und B.
A = {4; 5; 6} B = {2; 4; 6}.
Nach der Summenregel müssen wir nun P(C) = P(A ∪ B) = P(A) + P(B) – P(A ∩ B) berechnen.
Dazu benötigen wir die Ergebnismenge von (A ∩ B). (A ∩ B) = {4;6}.
Die Wahrscheinlichkeiten der einzelnen Ereignisse sind demnach:
P(A) = \dfrac {1}{6} + \dfrac {1}{6} + \dfrac {1}{6} = \dfrac {3}{6} = \dfrac {1}{2}
P(A ∩ B)= \dfrac {1}{6} + \dfrac {1}{6} = \dfrac {2}{6} = \dfrac {1}{3}
Damit wird die Wahrscheinlichkeit von C:
P(C) = P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= \dfrac {1}{2} + \dfrac {1}{2} - \dfrac {1}{3} = 1 - \dfrac {1}{3} = \dfrac {3}{3} - \dfrac {1}{3} = \dfrac {2}{3}
Die Richtigkeit des Ergebnisses lässt sich leicht überprüfen, indem wir die Ergebnismenge von C = (A ∪ B) bildet, und deren Wahrscheinlichkeit bestimmen.
C = (A ∪ B) = {2; 4; 5; 6} \Rightarrow P(C) = P(A ∪ B) = \dfrac {1}{6} + \dfrac {1}{6} + \dfrac {1}{6} + \dfrac {1}{6} = \dfrac {4}{6} = \underline{\underline {\dfrac {2}{3}}}
Übung 1 Oder Wahrscheinlichkeit:
Wir werfen einen Würfel einmal. Dann legen wir zwei Ereignisse fest.
A: Die Augenzahl ist größer als 4.
B: Die Augenzahl ist eine ungerade Zahl und größer als 1.
Anschließend legen wir neues Ereignis fest:
C: Die Augenzahl ist größer als 4 oder die Augenzahl ist eine ungerade Zahl und größer als 1.
Das Ereignis C ist eine Oder-Verknüpfung aus A und B.
Bestimmen Sie die Wahrscheinlichkeit für die Oder-Verknüpfung P ( C ).
Die Lösung dazu ist unten.
Beispiel Oder Wahrscheinlichkeit:
Wieder werfen wir einen Würfel einmal. Anschließend legen wir zwei Ereignisse fest.
A: Die Augenzahl ist kleiner als 4.
B: Die Augenzahl ist 4 oder 5.
Dann legen wir ein neues Ereignis fest:
C: Die Augenzahl ist kleiner als 4 oder die Augenzahl ist 4 oder 5.
Das Ereignis C ist eine Oder-Verknüpfung aus A und B.
Bestimme die Wahrscheinlichkeit P (C)!
Übung 2 Oder Wahrscheinlichkeit:
Wir ziehen eine Karte aus einem Spiel mit 32 Karten.
Welche Wahrscheinlichkeit hat das folgende Ereignis?
E: Die gezogene Karte ist eine Bildkarte oder eine Kreuzkarte.
Die Lösung hierzu ist unten.
Zusammenfassung der bisher bekannten Rechenregeln für Wahrscheinlichkeiten:
Wenn S die Ergebnismenge eines Zufallsexperiments ist:
- Für alle Ereignisse E gilt:
\color{red}{0 ≤ P(E) ≤ 1} \color{black}{} , wobei \quad P( \varnothing) = 0 \quad und \quad P(S) = 1 ist.
Mit anderen Worten: die Wahrscheinlichkeit für das Eintreten eines Ereignisses liegt zwischen 0 und 1 und kann nicht negativ sein. - Ist E = {e1; e2; … en}, dann gilt:
P(E) = P(e1) + P(e2) + … + P(en)
Schau dir dazu das Beispiel mit dem Würfel an! - Für alle Ereignisse A und B gilt:
P(C) = P(A ∪ B) = P(A) + P(B) – P(A ∩ B) - Für alle Ereignisse C gilt:
P(({\overline A}) = 1 - P(C)
Das heißt, die Wahrscheinlichkeit für das Ereignise und das Gegenereignis ergänzen sich zu 1.
Das kannst du in dem Beitrag Ereignisse in der Wahrscheinlichkeitsrechnung nachlesen. Und du kannst dir dazu das das 📽️Video Ereignis und Gegenereignis ansehen. Außerdem das 📽️Video Ereignis und Gegenereignis Beispiele.
Lösung der Übung 1:
Wir werfen wieder einen Würfel einmal. Dann legen wir zwei Ereignisse fest.
A: Die Augenzahl ist größer als 4.
B: Die Augenzahl ist eine ungerade Zahl und größer als 1.
Anschließend legen wir ein neues Ereignis fest:
C: Die Augenzahl ist größer als 4 oder die Augenzahl ist eine ungerade Zahl und größer als 1.
Das Ereignis C ist eine Oder-Verknüpfung aus A und B.
Bestimme die Wahrscheinlichkeit P ( C )!
Die Lösung hierzu ist:
Zuerst bilden wir die Ergebnismengen von A und B.
A = {5; 6} B = {3; 5}.
Nach der Summenregel müssen wir nun P(C) = P(A ∪ B) = P(A) + P(B) – P(A ∩ B) berechnen.
Dazu benötigen wir die Ergebnismenge von (A ∩ B). (A ∩ B) = {5}.
Die Wahrscheinlichkeiten der einzelnen Ereignisse sind demnach:
P(A) = \dfrac {1}{6} + \dfrac {1}{6} = \dfrac {2}{6} = \dfrac {1}{3}
P(A ∩ B)= \dfrac {1}{6}
Damit wird die Wahrscheinlichkeit von C:
P(C) = P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= \dfrac {1}{3} + \dfrac {1}{3} - \dfrac {1}{6} = \dfrac {2}{6} + \dfrac {2}{6} - \dfrac {1}{6} = \dfrac {3}{6} = \underline{\underline {\dfrac {1}{2}}}
Die Richtigkeit des Ergebnisses lässt sich leicht überprüfen, indem wir die Ergebnismenge von C = (A ∪ B) bildet, und deren Wahrscheinlichkeit bestimmen.
C = (A ∪ B) = {3; 5; 6} \Rightarrow P(C) = P(A ∪ B) = \dfrac {1}{6} + \dfrac {1}{6} + \dfrac {1}{6} = \dfrac {3}{6} = \underline{\underline {\dfrac {1}{2}}}
Lösung der Übung 2:
Wir ziehen eine Karte aus einem Spiel mit 32 Karten.
Welche Wahrscheinlichkeit hat das folgende Ereignis?
E: Die gezogene Karte ist eine Bildkarte oder eine Kreuzkarte.
Die Lösung hierzu ist:
Das Ereignis E ist eine Oder-Verknüpfung aus den Ereignissen
A: Die gesuchte Karte ist eine Bildkarte und
B: Die gesuchte Karte ist eine Kreuzkarte.
Zuerst bestimmen wir die Anzal der möglichen Ergebnisse von A und B.
A: Es gibt 12 Bildkarten von insgesamt 32 Karten.
B: Es gibt 8 Kreuzkarten von insgesamt 32 Karten.
Nach der Summenregel müssen wir nun P(C) = P(A ∪ B) = P(A) + P(B) – P(A ∩ B) berechnen.
Dazu benötigen wir noch die Anzahl der möglichen Ergebnisse von A ∩ B.
A ∩ B: Es gibt 3 Kreuz-Bildkarten (Bube, Dame, König).
Die Wahrscheinlichkeit der einzelnen Ereignisse sind:
P(A) = \dfrac {12}{32} P(B) = \dfrac {8}{32} .
P(A ∩ B)= \dfrac {3}{32} .
Damit wird die Wahrscheinlichkeit von C:
P(C) = P(A ∪ B) = P(A) + P(B) – P(A ∩ B)=
\dfrac {12}{32} + \dfrac {8}{32} - \dfrac {3}{32} = \underline{\underline {\dfrac {17}{23}}} .
Die Richtigkeit des Ergebnisses lässt sich leicht überprüfen, indem wir die Ergebnismenge von C = (A ∪ B) bildet, und deren Wahrscheinlichkeit bestimmen.
Das in der Mengenschreibweise darzustellen, ist sehr umständlich. Wir wissen jedoch, dass es 12 Bildkarten und 8 Kreuzkarten gibt, wobei es 3 Kreuz-Bildkarten (Bube, Dame, König) gibt. Also gibt es 12 + 8 – 3 Bild- oder Kreuzkarten.
\Rightarrow P(C) = P(A ∪ B) = \dfrac {12}{32} + \dfrac {8}{32} - \dfrac {3}{32} = \underline{\underline {\dfrac {17}{32}}}
Im nächsten Beitrag beschäftigen wir uns damit, wann ein Ereignis in der Wahrscheinlichkeitsrechnung abhängig und wann es unabhängig von einem anderen Ereignis ist. Außerdem wie dies mathematisch berechnet wird. Mit anderen Worten, die Bedingte Wahrscheinlichkeit.
Dazu findest du hier eine Übersicht über alle Beiträge zum Thema Wahrscheinlichkeitsrechnung. Darin auch Links zu Aufgaben.
Dazu kannst du auch den Wikipedia-Artikel Ereignis (Wahrscheinlichkeitstheorie) lesen.
